Envelope function
- See also: Modulation
In physics and engineering, the envelope function of a rapidly varying signal is a smooth curve outlining its extremes in amplitude.[1] The figure illustrates a sine wave varying between an upper and a lower envelope. The envelope function may be a function of time, or of space, or indeed of any variable.
Example: Beating waves
- See also: Beat (acoustics)
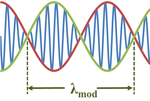
A common situation resulting in an envelope function in both space x and time t is the superposition of two waves of almost the same wavelength and frequency:[2]
which uses the trigonometric formula for the addition of two sine waves, and the approximation Δλ<<λ:
Here the modulation wavelength λmod is given by:[2][3]
The modulation wavelength is double that of the envelope itself because each half-wavelength of the modulating cosine wave governs both positive and negative values of the modulated sine wave. Likewise the beat frequency is that of the envelope, twice that of the modulating wave, or 2Δf.[4]
If this wave is a sound wave, the ear hears the frequency associated with f and the amplitude of this sound varies with the beat frequency.[4]
Phase and group velocity
The argument of the sinusoids above apart from a factor 2π are:
with subscripts c and e referring to the carrier and the envelope. The same amplitude F of the wave results for the same value of ξc and ξb, even though this value results for different choices of x and t. This invariance means that one can trace these waveforms in space to find how a position of fixed amplitude propagates in time with a speed that keeps ξ fixed; that is, for the carrier:
which determines for a constant amplitude the distance Δx is related to the time interval Δt by the so-called phase velocity vp
On the other hand, the same considerations show the envelope propagates at the so-called group velocity vg:[5]
A more common expression for the group velocity is obtained by introducing the wavevector k:
We notice that for small changes Δλ, the magnitude of the corresponding small change in wavevector:
so the group velocity can be rewritten as:
In all media, frequency and wavevector are related by a dispersion relation, 2πf ≡ ω = ω(k), and the group velocity can be written:
Here ω is the frequency in radians/s. In a medium such as classical vacuum the dispersion relation for electromagnetic waves is:
where c0 is the speed of light in classical vacuum. For this case, the phase and group velocities both are c0. In so-called dispersive media the dispersion relation can be a complicated function of wavevector, and the phase and group velocities are not the same. In the general case, the phase and group velocities may have different directions.[6]
Example: Envelope function approximation

Electron probabilities in lowest two quantum states of a 160Ǻ GaAs quantum well in a GaAs-GaAlAs quantum heterostructure as calculated from envelope functions.[7]
In condensed matter physics the wavefunction for a mobile charge carrier in a crystal can be expressed as a Bloch wave:
where n is the index for the band (for example, conduction or valence band) r is the spatial location of the particle, and k is its wavevector. The exponential is a sinusoidally varying function corresponding to a slowly varying envelope modulating the rapidly varying part of the wavefunction u, describing the behavior of the wavefunction close to the cores of the atoms of the lattice.
In determining the behavior of the carriers using quantum mechanics, the envelope approximation usually is used in which the Schrödinger equation is simplified to refer only to the behavior of the envelope, and boundary conditions are applied to the envelope function directly, rather than to the complete wavefunction.[8] For example, the wavefunction of a carrier trapped near an impurity is governed by an envelope function F that becomes a superposition of Bloch envelope functions:
where the coefficients A(k) are found from the approximate Schrödinger equation, and V is the crystal volume.[9]
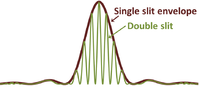
Example: Diffraction patterns
Diffraction patterns from multiple slits have envelopes determined by the single slit diffraction pattern. For a single slit the pattern is given by:[10]
where α is the diffraction angle, d is the slit width, and λ is the wavelength. For multiple slits, the pattern is [10]
where q is the number of slits, and g is the grating constant. The first factor, the single-slit result, modulates the more rapidly varying second factor that depends upon the number of slits and their spacing.
Example: Sound envelope
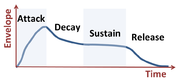
The amplitude of a musical note varies in time according to its sound envelope.[11]
A musical instrument playing a musical note produces a tone, which is a superposition of various frequencies with various amplitudes and phases that give each instrument its unique character. The manner of play determines the sound envelope of the frequencies in the tone, and governs the amplitude of the tone in time. By controlling the sound envelope, each musician imparts their particular interpretation of the music.
References
- ↑ C. Richard Johnson, Jr, William A. Sethares, Andrew G. Klein (2011). “Figure C.1: The envelope of a function outlines its extremes in a smooth manner”, Software Receiver Design: Build Your Own Digital Communication System in Five Easy Steps. Cambridge University Press, p. 417. ISBN 0521189446.
- ↑ Jump up to: 2.0 2.1 Blair Kinsman (2002). Wind Waves: Their Generation and Propagation on the Ocean Surface, Reprint of Prentice-Hall 1965. Courier Dover Publications, p. 186. ISBN 0486495116.
- ↑ Mark W. Denny (1993). Air and Water: The Biology and Physics of Life's Media. Princeton University Press, p. 289. ISBN 0691025185.
- ↑ Jump up to: 4.0 4.1 Paul Allen Tipler, Gene Mosca (2008). Physics for Scientists and Engineers, Volume 1, 6th ed. Macmillan, p. 538. ISBN 142920124X.
- ↑ Peter W. Milonni, Joseph H. Eberly (2010). “§8.3 Group velocity”, Laser Physics, 2nd ed. John Wiley & Sons, p. 336. ISBN 0470387718.
- ↑ V. Cerveny, Vlastislav Červený (2005). “§2.2.9 Relation between the phase and group velocity vectors”, Seismic Ray Theory. Cambridge University Press, p. 35. ISBN 0521018226.
- ↑ G Bastard, JA Brum, R Ferreira (1991). “Figure 10 in Electronic States in Semiconductor Heterostructures”, Henry Ehrenreich, David Turnbull, eds: Solid state physics: Semiconductor Heterostructures and Nanostructures. ISBN 0126077444.
- ↑ Christian Schüller (2006). “§2.4.1 Envelope function approximation (EFA)”, Inelastic Light Scattering of Semiconductor Nanostructures: Fundamentals And Recent Advances. Springer, p. 22. ISBN 3540365257.
- ↑ For example, see Giuseppe Grosso, Giuseppe Pastori Parravicini (2000). Solid State Physics, 6th ed. Academic Press, p. 478. ISBN 012304460X.
- ↑ Jump up to: 10.0 10.1 Kordt Griepenkerl (2002). “Intensity distribution for diffraction by a slit and Intensity pattern for diffraction by a grating”, John W Harris, Walter Benenson, Horst Stöcker, Holger Lutz, editors: Handbook of physics. Springer, pp. 306 ff. ISBN 0387952691.
- ↑ Stanley R. Alten (2010). “Sound envelope”, Audio in Media, 12th ed. Cengage Learning, p. 13. ISBN 049557239X.

![{\displaystyle F(x,\ t)=\sin \left[2\pi \left({\frac {x}{\lambda -\Delta \lambda }}-(f+\Delta f)t\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0467cdce58d41ddf370525c035d69f994c3f10a4)
![{\displaystyle +\sin \left[2\pi \left({\frac {x}{\lambda +\Delta \lambda }}-(f-\Delta f)t\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/987cb6c9153bdae25867ffef6107a03ecc677376)
![{\displaystyle \approx 2\cos \left[2\pi \left({\frac {x}{\lambda _{mod}}}-\Delta f\ t\right)\right]\ \sin \left[2\pi \left({\frac {x}{\lambda }}-f\ t\right)\right]\ ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe71e240d4a8f95bb96ca9bfebc22f2be9fffabf)