Tone (music)
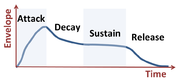
The amplitude of a musical note varies in time according to its sound envelope.[1]
A musical tone is the sound produced by a musical instrument playing a particular musical note. Tone is an objective (measurable) physical property of a note produced in a particular fashion. The differences in tone between musical instruments can be analyzed using Fourier series to identify the frequencies comprising the tone.[2]
The frequency spectrum of a musical instrument playing a particular note varies with the instrument and with the way that it is played. The manner of playing determines the sound envelope of a note, and therefore the amplitude of its constituent frequencies.[1] The spectrum is altered somewhat by the sound envelope, so the musician has some control over the tone.
Some instruments (like the flute or the violin) exhibit a fundamental frequency and multiples of that frequency called harmonics or overtones, all of various amplitudes and phases, and others (like the cymbal or the ratchet) do not.[2][3][4] These ideas find application in the construction of music synthesizers and musical instruments of all kinds.
The perception of a tone involves the subjective attributes called pitch and timbre, and listening to multiple tones can result in perception of either a chord, or a single note. These topics are pursued further below.
Helmholtz' theory
Hermann Ludwig F. von Helmholtz developed a theory for the perception of musical sounds.[5] However, apart from his ideas about perception, which involve conjectures about how the ear operates, Helmholtz commented upon the production of sound by musical instruments.
To understand Helmholtz' comments below, some vocabulary is needed: A single note is often referred to as a tone, the lowest frequency present as the fundamental or prime partial tone and harmonics (multiples) of this frequency that appear when a note is played on an instrument as harmonic upper partial tones or upper tones or upper partials. Where only one frequency is present, as with a tuning fork, it is called a simple tone or, sometimes, a pure tone. Where multiple frequencies are present, it is called a compound tone. So, a tone may be a pure tone or a compound tone.[5]
| It is well known that this union of several simple tones into one compound tone, which is naturally effected in the tones produced by most musical instruments, is artificially imitated on the organ by peculiar mechanical contrivances. The tones of organ-pipes are comparatively poor in upper partials. When it is desirable to use a stop of incisive penetrating quality of tone and great power, the wide pipes (principal register and weithgedackt) are not sufficient; their tone is too soft too defective in upper partials; and the narrow pipes (geigen-register and quintaten) are also unsuitable, because, although more incisive, their tone is weak. For such occasions, then, as in accompanying congregational singing, recourse is had to the compound stops. In these stops every key is connected with a large or smaller series of pipes, which it opens simultaneously, and which give the prime tone and a certain number of the first upper partials of the compound tone of the note in question. Helmholtz, p. 91[5] |
These words identify the organ as a form of mechanical rather than electronic music synthesizer. They also lay out the characterization of a musical note by its constituent frequency components, in the same way that a Fourier series expresses a periodic waveform in terms of its harmonic components.
Fourier series
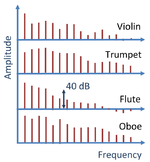
As the remarks of Helmholtz suggest, the sound of a note played upon each instrument is characterized by not only its fundamental tone or frequency, which is the same for all instruments, but by the higher partial tones or harmonics in the note, which are different in amplitude and in phase for each instrument, making them sound different. The figure shows the partial tones making up a tone in four instruments playing the same musical note. In addition to these partial tones, the spectrum contains a wide-band background of frequencies, not shown.
A musical note is a periodic function in time and in space, modulated by a sound envelope. That is, the note can be expressed in one spatial dimension as:
where s is the sound envelope that expresses the duration of the note at a fixed location or its extent in space at a fixed time, and f is a periodic function of its argument:
with λ the wavelength of f and T = λ/v the period of f and v the speed of propagation of f through space.
The periodic factor in such a wave can be analyzed using a Fourier series to show it is made up of a summation of sinusoidal waves, each with their own frequency. These frequency components are useful in distinguishing the different characteristics of the same note played upon different instruments, as shown approximately in the figure.
Pitch
A laboratory determination of pitch is made by a subject listening to a tone from a musical instrument and to a simple tone, such as that produced by a tuning fork, and identifying circumstances where the instrument and the simple tone sound alike.[6] As a result, pitch is not a purely objective physical property; it is a subjective psychoacoustical attribute of a sound.
Timbre
- See also: Music perception
Naturally, besides the tone produced by the instrument, the musical experience also depends upon how the tone is modified by the auditorium where it propagates, and how the ear responds to the tone.[7] These effects that relate to the propagation and the perception of a sound are separate from the production of sound by the instrument. The perceived quality of a tone is referred to as timbre. The American National Standards Institute definition of timbre describes it as "that attribute of auditory sensation in terms of which a listener can judge that two sounds similarly presented and having the same loudness and pitch are dissimilar", and a note to this definition adds that "timbre depends primarily upon the spectrum of the stimulus, but it also depends upon the waveform, the sound pressure, the frequency location of the spectrum, and the temporal characteristics of the stimulus" [8]
Chord
As a musical tone consists of a fundamental tone and higher partial tones, one might ask how this differs from a chord, that is, several tones played simultaneously. This question is fundamentally one of perception: for example, how is it that a note played on a musical instrument is heard with a particular timbre, while several notes sound not like a single note played upon a different instrument (a note with a single timbre), but like a chord (a combination of notes, each with their own timbre)?
The perceptions of chord and timbre are complex. Partly, the differences have to do with the reaction of the ear to loudness of the constituent frequencies, and the fusion of separate harmonics into a single whole is disturbed when some component frequencies gain an intensity comparable to the fundamental, resulting in the perception of a chord.[9][10] The differences also involve how the ear responds to the way the sounds evolve in time; commonality in time-variation of harmonics tends to be heard as the fusing of the harmonics into the timbre of one tone.[11]
References
- ↑ Jump up to: 1.0 1.1 Stanley R. Alten (2010). “Sound envelope”, Audio in Media, 12th ed. Cengage Learning, p. 13. ISBN 049557239X.
- ↑ Jump up to: 2.0 2.1 Leon Gunther (2011). The Physics of Music and Color. Springer, p. 47 ff. ISBN 1461405564. “...the frequency spectrum for the modes of vibration of a musical instrument that produces a well-defined pitch must be a harmonic series”
- ↑ Thomas D. Rossing (2007). “Figure 15.10: ...Spectrum for the sounds of the ratchet, cymbal and timpani”, Springer Handbook of Acoustics. Springer, p. 547. ISBN 0387304460. “The timpani spectrum shows a small number of large peaks corresponding to the prominent modes of vibration of the drum head superimposed on a very wide-band spectrum...”
- ↑ Bart Hopkin (1996). “Figure 2-4: Resonance response curves”, Musical Instrument Design: Practical Information for Instrument Making. See Sharp Press, p. 110. ISBN 1884365086.
- ↑ Jump up to: 5.0 5.1 5.2 Hermann Ludwig F. von Helmholtz (1875). On the sensations of tone as a physiological basis for the theory of music, Translation by Alexander John Ellis. Oxford University Press, p. 33.
- ↑ Thomas D. Rossing (2007). Springer Handbook of Acoustics. Springer, p. 477. ISBN 0387304460.
- ↑ David Martin Howard, Jamie Angus (2009). “§3.1.2 Musical notes and their harmonics”, Acoustics and Psychoacoustics, 4rth ed. Focal Press, pp. 124 ff. ISBN 0240521757.
- ↑ American Standard Acoustical Terminology S1.1-1960, p. 45. Update: ANSI S1.1-1994 (R2004) American National Standard Acoustical Terminology. This description is much quoted: see Petri Toiviainen (1996). "Optimizing auditory images and distance metrics for self-organizing timbre maps". Journal of Music Research 25: 1-30. DOI:10.1080/09298219608570695. Research Blogging. and Robert Erickson (1975). Sound Structure in Music. University of California Press, p. 4. ISBN 0520023765.
- ↑ Robert Erickson (1975). “Pitch (with timbre) → chord”, Sound Structure in Music. University of California Press, p. 20. ISBN 0520023765.
- ↑ Hugo Münsterberg (1914). Psychology, general and applied. Appleton, p. 90. “But if the tone of 100 vibrations is strong, while those others are weak, our immediate impression is not that of a manifoldness of tones combined in a chord, but that of one tone in a particular timbre.”
- ↑ J Chowning (2008). “Fifty years of computer music: ideas of the past speak to the future”, Richard Kronland-Martinet, Sølvi Ystad, Kristoffer Jensen, eds: Computer Music Modeling and Retrieval: Sense of Sounds:, 4th International Symposium, CMMR 2007, Copenhagen, Denmark, August 27-31, 2007. Springer, pp. 4-5. ISBN 3540850341. “Because all of the partials die away in a similar manner, they fuse and are heard as timbre rather than harmony.”