Green's function: Difference between revisions
imported>Paul Wormer No edit summary |
imported>Caesar Schinas m (Bot: Update image code) |
||
| (12 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
In [[physics]] and [[mathematics]], '''Green's | {{subpages}} | ||
In [[physics]] and [[mathematics]], '''Green's functions''' are auxiliary functions in the solution of linear partial [[differential equations]]. Green's function is named for the self-taught English mathematician [[George Green]] (1793 – 1841), who investigated electricity and magnetism in a thoroughly mathematical fashion. In 1828 Green published a privately printed booklet, introducing what is now called the Green function. This was ignored until [[William Thomson]] (Lord Kelvin) discovered it, recognized its great value and had it published nine years after Green's death. [[Bernhard Riemann]] gave it the name "Green function".<ref>M. Kline, ''Mathematical Thought from Ancient to Modern Times'', Oxford University Press, New York (1972) p. 683</ref> | |||
==Definition== | |||
Let ''L''<sub>'''''x'''''</sub> be a given linear differential operator in ''n'' variables '''''x''''' = (''x''<sub>1</sub>, ''x''<sub>2</sub>, ..., ''x''<sub>''n''</sub>), then the ''Green function of'' ''L''<sub>'''''x'''''</sub> is the function ''G''('''''x''''','''''y''''') defined by | Let ''L''<sub>'''''x'''''</sub> be a given linear differential operator in ''n'' variables '''''x''''' = (''x''<sub>1</sub>, ''x''<sub>2</sub>, ..., ''x''<sub>''n''</sub>), then the ''Green function of'' ''L''<sub>'''''x'''''</sub> is the function ''G''('''''x''''','''''y''''') defined by | ||
:<math> | :<math> | ||
L_\mathbf{x} G(\mathbf{x},\mathbf{y}) = | L_\mathbf{x} G(\mathbf{x},\mathbf{y}) = \delta(\mathbf{x}- \mathbf{y}), | ||
</math> | </math> | ||
where δ('''''x'''''-'''''y''''') is the [[Dirac delta function]]. Once ''G''('''''x''''','''''y''''') is known, any differential equation involving ''L''<sub>'''''x'''''</sub> is formally solved, | where δ('''''x'''''-'''''y''''') is the [[Dirac delta function]]. Once ''G''('''''x''''','''''y''''') is known, any differential equation involving ''L''<sub>'''''x'''''</sub> is formally solved. Suppose we want to solve, | ||
:<math> | |||
L_\mathbf{x} \,\phi(\mathbf{x}) = \rho(\mathbf{x}) | |||
</math> | |||
for a known right hand side ρ('''''x'''''). | |||
The formal solution is | |||
:<math> | :<math> | ||
\phi(\mathbf{x}) = \int\; G(\mathbf{x},\mathbf{y})\; \rho(\mathbf{y})\; \mathrm{d}\mathbf{y}. | \phi(\mathbf{x}) = \int\; G(\mathbf{x},\mathbf{y})\; \rho(\mathbf{y})\; \mathrm{d}\mathbf{y}. | ||
</math> | </math> | ||
The proof is by verification, | The proof is by verification, | ||
:<math> | :<math> | ||
L_\mathbf{x} \,\phi(\mathbf{x}) = \int\;L_\mathbf{x} \; G(\mathbf{x},\mathbf{y})\; \rho(\mathbf{y})\; \mathrm{d}\mathbf{y} = | L_\mathbf{x} \,\phi(\mathbf{x}) = \int\;L_\mathbf{x} \; G(\mathbf{x},\mathbf{y})\; \rho(\mathbf{y})\; \mathrm{d}\mathbf{y} = \int\;\delta(\mathbf{x}- \mathbf{y})\;\rho(\mathbf{y}) \mathrm{d}\mathbf{y} = \rho(\mathbf{x}) | ||
</math> | </math> | ||
where in the last step the defining property of the Dirac delta function is used. | where in the last step the defining property of the Dirac delta function is used. | ||
The Green function | The integral operator that has the Green function as kernel may be seen as the inverse of a linear operator, | ||
:<math> | |||
L_\mathbf{x}\;\phi(\mathbf{x}) = \rho(\mathbf{x}) \quad\Longrightarrow \quad \phi( \mathbf{x}) =L_\mathbf{x}^{-1}\;\rho(\mathbf{x}) = \int G(\mathbf{x},\mathbf{y}) \rho(\mathbf{y})\;\mathrm{d}\mathbf{y} . | |||
</math> | |||
It is illuminating to make the analogy with matrix equations. Let <math>\mathbb{L}</math> and <math>\mathbb{G}</math> be ''n''×''n'' matrices connected by | |||
:<math> | :<math> | ||
\mathbb{L} \mathbb{G} = \mathbb{ | \mathbb{L} \mathbb{G} = \mathbb{E}\quad \Longleftrightarrow \quad \left(\mathbb{L} \mathbb{G}\right)_{ij} = \delta_{ij}, \quad\hbox{i.e.,}\quad \mathbb{G} = \mathbb{L}^{-1}, | ||
</math> | </math> | ||
then the solution of | then the solution of a matrix-vector equation is | ||
:<math> | :<math> | ||
\mathbb{L}\boldsymbol{\phi} = | \mathbb{L}\boldsymbol{\phi} = \boldsymbol{\rho}\quad \Longrightarrow \quad | ||
\ | \phi_i = \sum_{j} \mathbb{G}_{ij} \rho_j. | ||
</math> | </math> | ||
Make the correspondence ''i'' ↔ '''''x''''', ''j'' ↔ '''''y''''', and compare the sum over ''j'' with the integral over '''''y''''', and the correspondence is evident. | |||
==Example== | |||
We consider a case of three variables, ''n'' = 3 with '''''x''''' = (''x'', ''y'', ''z''). | |||
The Green function of | |||
:<math> | |||
\nabla^2 \equiv | |||
\left( \frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2}\right) | |||
</math> | |||
is | |||
:<math> | |||
G(\mathbf{x},\mathbf{y}) = -\frac{1}{4\pi} \frac{1}{|\mathbf{x}-\mathbf{y}|}. | |||
</math> | |||
As an important example of this Green function we mention that the formal solution of the [[Poisson equation]] of electrostatics, reading | |||
:<math> | |||
\nabla^2 \Phi(\mathbf{x}) = -\frac{1}{\epsilon_0} \rho(\mathbf{x}), | |||
</math> | |||
where ε<sub>0</sub> is the [[electric constant]] and ρ is a charge distribution, | |||
is given by | |||
:<math> | |||
\Phi(\mathbf{x}) = \frac{1}{4\pi \epsilon_0} \iiint\; \frac{\rho(\mathbf{y})}{|\mathbf{x}-\mathbf{y}|} | |||
\;\mathrm{d}\mathbf{y}. | |||
</math> | |||
Indeed, | |||
:<math> | |||
\nabla^2 \Phi(\mathbf{x}) = \frac{1}{4\pi \epsilon_0} \iiint\; \rho(\mathbf{y}) \nabla^2\frac{1}{|\mathbf{x}-\mathbf{y}|} \;\mathrm{d}\mathbf{y} = -\frac{4\pi}{4\pi\epsilon_0} | |||
\iiint\; \rho(\mathbf{y}) \delta(\mathbf{x}-\mathbf{y}) \;\mathrm{d}\mathbf{y} = -\frac{\rho(\mathbf{x})}{\epsilon_0}. | |||
</math> | |||
The integral form of the electrostatic field may be seen as a consequence of [[Coulomb's law]]. The field at the point '''''x''''' due to the charge d''Q'' = ρ('''''y''''')d'''''y''''' is equal to | |||
:<math> | |||
d\Phi(\mathbf{x}) = \frac{dQ}{4\pi\epsilon_0 |\mathbf{x}-\mathbf{y}|}. | |||
</math> | |||
The field is additive in the charges, so integration gives the total field at '''''x'''''. | |||
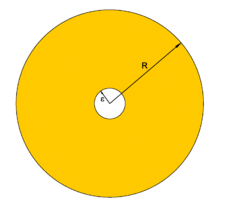
{{Image|Green delta.png|right|225px|Integration regions: yellow domain is ''U''<sub>ε</sub>, large sphere is ''V''<sub>''R''</sub>, small sphere is ''V''<sub>ε</sub>}} | |||
===Proof of Green function of ∇<sup>2</sup>=== | |||
Without loss of generality we take '''''x''''' as the origin (0, 0, 0) and replace '''''y''''' by '''''r''''' = (''x'', ''y'', ''z'') in the above formulation. The length of '''''r''''' is indicated by ''r''. | |||
The proof uses [[Green's Theorem#Statement in three dimensions|Green's theorem]]: | |||
:<math> | |||
\iiint\limits_{V_a} \Big( \phi \nabla^2\frac{1}{r} - \frac{1}{r} \nabla^2\phi\Big)\, d V = | |||
\iint\limits_{S_a} \big(\phi \boldsymbol{\nabla}\frac{1}{r}\big) \cdot d\mathbf{S} - \iint\limits_{S_a} \big(\frac{1}{r} \boldsymbol{\nabla}\phi\big) \cdot d\mathbf{S}, | |||
</math> | |||
where ''V''<sub>''a''</sub> is a sphere with radius ''a'' and ''S''<sub>''a''</sub> is the surface of this sphere. The smooth test function φ and its gradient vanish for large ''r'', | |||
:<math> | |||
\phi(x,y,z) =0, \quad \boldsymbol{\nabla}\phi(x,y,z) = \mathbf{0}\quad \hbox{for}\quad r \ge R \quad\hbox{with}\quad r \equiv \sqrt{x^2+y^2+z^2}. | |||
</math> | |||
Further we notice that | |||
:<math> | |||
\nabla^2 \frac{1}{r} = 0\quad \hbox{for}\quad r \in U_\epsilon, | |||
</math> | |||
because ''r'' ≠ 0 in that region (see the figure, where the region is indicated in yellow). | |||
This result is most easily proved if we recall that in [[Spherical polar coordinates#Differential operators|spherical polar coordinates]] | |||
:<math> | |||
\nabla^2\frac{1}{r} = \frac{1}{r} \frac{\partial^2 r}{\partial r^2} \frac{1}{r} = \frac{1}{r} \frac{\partial^2 }{\partial r^2} 1 = 0. | |||
</math> | |||
First apply Green's theorem to the large sphere of radius ''R'' | |||
:<math> | |||
\iiint\limits_{V_R} \phi \nabla^2\frac{1}{r}\, d V = \iiint\limits_{V_R} \frac{1}{r} \nabla^2\phi\, d V + | |||
\iint\limits_{S_R} \big(\phi \boldsymbol{\nabla}\frac{1}{r}\big) \cdot d\mathbf{S} - \iint\limits_{S_R} \big(\frac{1}{r} \boldsymbol{\nabla}\phi\big) \cdot d\mathbf{S} = | |||
\iiint\limits_{V_R} \frac{1}{r} \nabla^2\phi\, d V | |||
</math> | |||
because by assumption φ and its gradient vanish on ''S''<sub>''R''</sub>. | |||
We consider the integral on the right hand side and we will show that | |||
:<math> | |||
\iiint\limits_{V_R} \frac{1}{r} \nabla^2\phi\, d V = -4\pi \phi(\mathbf{0}), | |||
</math> | |||
from which the result to be proved follows directly. The main trick is to write | |||
:<math> | |||
\iiint\limits_{V_R} \frac{1}{r} \nabla^2\phi\, d V = \lim_{\epsilon \rightarrow 0} \iiint\limits_{U_\epsilon} \frac{1}{r} \nabla^2\phi\, d V | |||
</math> | |||
and to consider first the integral over ''U''<sub>ε</sub> (the yellow domain in the figure) for non-zero, but small, ε. After the integral has been evaluated, the limit for zero ε is taken. | |||
Since ''U''<sub>ε</sub> has two surfaces, Green's theorem cannot be applied directly, and therefore we write (see the figure), | |||
:<math> | |||
\iiint\limits_{U_\epsilon} = \iiint\limits_{V_R} - \iiint\limits_{V_\epsilon} | |||
</math> | |||
and apply Green's theorem to the two terms. Recalling that we saw already the first term, we get | |||
:<math> | |||
\begin{align} | |||
\iiint\limits_{U_\epsilon} \frac{1}{r} \nabla^2\phi\, d V &= | |||
\left[ \iiint\limits_{V_R} \phi \nabla^2\frac{1}{r}\, d V - \iiint\limits_{V_\epsilon} \phi \nabla^2\frac{1}{r}\, d V \right] | |||
+\iint\limits_{S_\epsilon} \big(\phi \boldsymbol{\nabla}\frac{1}{r}\big) \cdot d\mathbf{S} - \iint\limits_{S_\epsilon} \big(\frac{1}{r} \boldsymbol{\nabla}\phi\big) \cdot d\mathbf{S}\\ | |||
&= \left[\iiint\limits_{U_\epsilon} \phi \nabla^2\frac{1}{r}\, d V \right] +\iint\limits_{S_\epsilon} \big(\phi \boldsymbol{\nabla}\frac{1}{r}\big) \cdot d\mathbf{S} - \iint\limits_{S_\epsilon} \big(\frac{1}{r} \boldsymbol{\nabla}\phi\big) \cdot d\mathbf{S}\\ | |||
\end{align} | |||
</math> | |||
The integral between square brackets is zero because ∇<sup>2</sup>(1/''r'') is zero on ''U''<sub>ε</sub>. The last integral can be shown to vanish for small ε. Because φ and its gradient are smooth and finite, and ''r'' is constant (equal to ε) on the surface, we may write for small ε | |||
:<math> | |||
\iint\limits_{S_\epsilon} \big(\frac{1}{r} \boldsymbol{\nabla}\phi\big) \cdot d\mathbf{S} | |||
\approx \frac{\langle\mathbf{n}\cdot \boldsymbol{\nabla}\phi(\epsilon)\rangle}{\epsilon} \iint\limits_{S_\epsilon}dS = 4\pi \epsilon \langle\mathbf{n}\cdot \boldsymbol{\nabla}\phi(\epsilon)\rangle \rightarrow 0, | |||
</math> | |||
where we assumed that | |||
:<math> | |||
\boldsymbol{\nabla}\phi(\mathbf{r})\cdot d\mathbf{S} = \boldsymbol{\nabla}\phi(\mathbf{r})\cdot\mathbf{n}\;dS \approx \langle \boldsymbol{\nabla}\phi(\epsilon)\cdot\mathbf{n}\rangle \;dS | |||
</math> | |||
and that the value of the gradient averaged over the surface may be taken out of the integral. The remaining surface integral is equal to 4πε<sup>2</sup>. | |||
In order to evaluate the final integral we use | |||
:<math> | |||
\boldsymbol{\nabla} \frac{1}{r} = - \frac{\mathbf{r}}{r^3} \equiv -\frac{\mathbf{e}_r}{r^2} \qquad | |||
\hbox{and}\qquad d\mathbf{S} = \mathbf{e}_r \;r^2\sin\theta\,d\phi d\theta | |||
</math> | |||
so that | |||
:<math> | |||
\iint\limits_{S_\epsilon} \big(\phi \boldsymbol{\nabla}\frac{1}{r}\big) \cdot d\mathbf{S} | |||
= | |||
-\iint\limits_{S_\epsilon} \phi(\mathbf{r}) \sin\theta\,d\phi d\theta = -\phi(\epsilon) \; 4\pi. | |||
</math> | |||
Here we assumed that the test function φ('''''r''''') is constant over the surface (isotropic) for small ε. The limit ε → 0 gives the desired result. | |||
Summarizing, | |||
:<math> | |||
\iiint\limits_{V_R} \phi \nabla^2\frac{1}{r}\, d V = | |||
\iiint\limits_{V_R} \frac{1}{r} \nabla^2\phi\, d V = | |||
-4\pi \phi(\mathbf{0}) = | |||
-4\pi \iiint\limits_{V_R} \delta(\mathbf{r}) \phi(\mathbf{r}) \, d V, | |||
</math> | |||
and | |||
<table border="2" align="center" rules="all" cellpadding="10%"> | |||
<tr><td><math> | |||
\nabla^2\frac{1}{r} = - 4\pi \delta(\mathbf{r}) | |||
</math> | |||
</table> | |||
== | ==References== | ||
P. Roman, ''Advanced Quantum Theory'', Addison-Wesley, Reading, Mass. (1965) Appendix 4. | <references /> | ||
* P. Roman, ''Advanced Quantum Theory'', Addison-Wesley, Reading, Mass. (1965) Appendix 4. | |||
* I. M. Gel'fand and G. E. Shilov, ''Generalized Functions'', Vol. 1, Academic Press, New York (1964) | |||
Latest revision as of 12:22, 11 June 2009
In physics and mathematics, Green's functions are auxiliary functions in the solution of linear partial differential equations. Green's function is named for the self-taught English mathematician George Green (1793 – 1841), who investigated electricity and magnetism in a thoroughly mathematical fashion. In 1828 Green published a privately printed booklet, introducing what is now called the Green function. This was ignored until William Thomson (Lord Kelvin) discovered it, recognized its great value and had it published nine years after Green's death. Bernhard Riemann gave it the name "Green function".[1]
Definition
Let Lx be a given linear differential operator in n variables x = (x1, x2, ..., xn), then the Green function of Lx is the function G(x,y) defined by
where δ(x-y) is the Dirac delta function. Once G(x,y) is known, any differential equation involving Lx is formally solved. Suppose we want to solve,
for a known right hand side ρ(x). The formal solution is
The proof is by verification,
where in the last step the defining property of the Dirac delta function is used.
The integral operator that has the Green function as kernel may be seen as the inverse of a linear operator,
It is illuminating to make the analogy with matrix equations. Let and be n×n matrices connected by
then the solution of a matrix-vector equation is
Make the correspondence i ↔ x, j ↔ y, and compare the sum over j with the integral over y, and the correspondence is evident.
Example
We consider a case of three variables, n = 3 with x = (x, y, z).
The Green function of
is
As an important example of this Green function we mention that the formal solution of the Poisson equation of electrostatics, reading
where ε0 is the electric constant and ρ is a charge distribution, is given by
Indeed,
The integral form of the electrostatic field may be seen as a consequence of Coulomb's law. The field at the point x due to the charge dQ = ρ(y)dy is equal to
The field is additive in the charges, so integration gives the total field at x.
Proof of Green function of ∇2
Without loss of generality we take x as the origin (0, 0, 0) and replace y by r = (x, y, z) in the above formulation. The length of r is indicated by r.
The proof uses Green's theorem:
where Va is a sphere with radius a and Sa is the surface of this sphere. The smooth test function φ and its gradient vanish for large r,
Further we notice that
because r ≠ 0 in that region (see the figure, where the region is indicated in yellow). This result is most easily proved if we recall that in spherical polar coordinates
First apply Green's theorem to the large sphere of radius R
because by assumption φ and its gradient vanish on SR.
We consider the integral on the right hand side and we will show that
from which the result to be proved follows directly. The main trick is to write
and to consider first the integral over Uε (the yellow domain in the figure) for non-zero, but small, ε. After the integral has been evaluated, the limit for zero ε is taken.
Since Uε has two surfaces, Green's theorem cannot be applied directly, and therefore we write (see the figure),
and apply Green's theorem to the two terms. Recalling that we saw already the first term, we get
The integral between square brackets is zero because ∇2(1/r) is zero on Uε. The last integral can be shown to vanish for small ε. Because φ and its gradient are smooth and finite, and r is constant (equal to ε) on the surface, we may write for small ε
where we assumed that
and that the value of the gradient averaged over the surface may be taken out of the integral. The remaining surface integral is equal to 4πε2.
In order to evaluate the final integral we use
so that
Here we assumed that the test function φ(r) is constant over the surface (isotropic) for small ε. The limit ε → 0 gives the desired result.
Summarizing,
and
References
- ↑ M. Kline, Mathematical Thought from Ancient to Modern Times, Oxford University Press, New York (1972) p. 683
- P. Roman, Advanced Quantum Theory, Addison-Wesley, Reading, Mass. (1965) Appendix 4.
- I. M. Gel'fand and G. E. Shilov, Generalized Functions, Vol. 1, Academic Press, New York (1964)























![{\displaystyle {\begin{aligned}\iiint \limits _{U_{\epsilon }}{\frac {1}{r}}\nabla ^{2}\phi \,dV&=\left[\iiint \limits _{V_{R}}\phi \nabla ^{2}{\frac {1}{r}}\,dV-\iiint \limits _{V_{\epsilon }}\phi \nabla ^{2}{\frac {1}{r}}\,dV\right]+\iint \limits _{S_{\epsilon }}{\big (}\phi {\boldsymbol {\nabla }}{\frac {1}{r}}{\big )}\cdot d\mathbf {S} -\iint \limits _{S_{\epsilon }}{\big (}{\frac {1}{r}}{\boldsymbol {\nabla }}\phi {\big )}\cdot d\mathbf {S} \\&=\left[\iiint \limits _{U_{\epsilon }}\phi \nabla ^{2}{\frac {1}{r}}\,dV\right]+\iint \limits _{S_{\epsilon }}{\big (}\phi {\boldsymbol {\nabla }}{\frac {1}{r}}{\big )}\cdot d\mathbf {S} -\iint \limits _{S_{\epsilon }}{\big (}{\frac {1}{r}}{\boldsymbol {\nabla }}\phi {\big )}\cdot d\mathbf {S} \\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe23b682772a037b0453c03e020506a09bf82273)





