Archive:New Draft of the Week
The New Draft of the Week is a chance to highlight a recently created Citizendium article that has just started down the road of becoming a Citizendium masterpiece.
It is chosen each week by vote in a manner similar to that of its sister project, the Article of the Week.
Add New Nominees Here
To add a new nominee or vote for an existing nominee, click edit for this section and follow the instructions
| Nominated article | Vote Score |
Supporters | Specialist supporters | Date created |
|---|---|---|---|---|
| Tall tale | 3 | Daniel Mietchen; Howard C. Berkowitz; Paul Wormer; |
9 March 2010 | |
| Plane (geometry) | 5 | Daniel Mietchen ; Meg Ireland; Chunbum Park; |
Peter Schmitt | Major rewrite on 29 March 2010 |
| Aeneid | 1 | Daniel Mietchen 23:38, 10 April 2010 (UTC) | 28 March 2010 | |
If you want to see how these nominees will look on the CZ home page (if selected as a winner), scroll down a little bit.
Transclusion of the above nominees (to be done by an Administrator)
- Transclude each of the nominees in the above "Table of Nominee" as per the instructions at Template:Featured Article Candidate.
- Then add the transcluded article to the list in the next section below, using the {{Featured Article Candidate}} template.
View Current Transcluded Nominees (after they have been transcluded by an Administrator)
The next New Draft of the Week will be the article with the most votes at 1 AM UTC on Thursday, 15 April, 2010.
| Nominated article | Supporters | Specialist supporters | Dates | Score | ||||
|---|---|---|---|---|---|---|---|---|
This article is about the geometrical concept. For other uses of the term Plane, please see Plane (disambiguation).
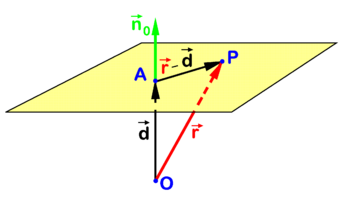
In Euclidean geometry, a plane is an abstract concept that models the common notion of a flat surface — without depressions, protrusions, holes and a boundary — that for any two of its points entirely contains the straight line joining them. Assuming a common (intuitive, physical) idea of the geometry of space, "plane" can be defined in terms of distances, orthogonality, lines, coordinates etc. In a more abstract approach (vector spaces) planes are defined as two-dimensional affine subspaces. In an axiomatic approach, basic concepts of elementary geometry, such as "point", "line" and "plane", are undefined primitives.  (CC) Image: Dina Tsirelson The surface of this metallic body consists of rectangles situated in various planes. Non-axiomatic approachDefinitionsA remarkTo define a plane is more complicated than it may seem. It is tempting to define a plane as a surface with zero curvature, where a surface is defined as a geometric object having length and breadth but no depth. However, this is not a good idea; such definitions are useless in mathematics, since they cannot be used when proving theorems. Planes are treated by elementary geometry, but the notions of surface and curvature are not elementary, they need more advanced mathematics and more sophisticated definitions. Fortunately, it is possible to define a line via more elementary notions, and this way is preferred in mathematics. Still, the definitions given below are tentative. They are criticized afterwards, see axiomatic approach. The definitions of "plane" given below may be compared with the definition of a circle as consisting of those points in a plane that are a given distance (the radius) away from a given point (the center). A circle is a set of points chosen according to their relation to some given parameters (center and radius). Similarly, a plane is a set of points chosen according to their relation to some given objects (points, lines etc). However, a circle determines its center and radius uniquely; for a plane, the situation is different. Four equivalent definitions of "plane" are given below. Any other definition is equally acceptable provided that it is equivalent to these. Note that a part of a plane is not a plane. Likewise, a line segment is not a line. Below, all points, lines and planes are situated in the space (assumed to be a three-dimensional Euclidean space), and by lines we mean straight lines. Definition via distancesLet two different points A and B be given. The set of all points C that are equally far from A and B — that is, — is a plane. This is the plane orthogonal to the line AB through the middle point of the line segment AB. Definition via right angles (orthogonality)Let two different points A and B be given. The set of all points C such that the lines AB and AC are orthogonal (that is, the angle BAC is right) is a plane. This is the plane orthogonal to the line AB through the point A. Definition via linesLet three points A, B and C be given, not lying on a line. Consider the lines DE for all points D (different from B) on the line AB and all points E (also different from B) on the line BC. The union of all these lines, together with the point B, is a plane. This is the plane through A, B and C. In other words, this plane is the set of all points F such that either F coincides with B or there exists a line through F that intersects the lines AB and BC (in distinct points). Definition via Cartesian coordinatesIn terms of Cartesian coordinates x, y, z ascribed to every point of the space, a plane is the set of points whose coordinates satisfy the linear equation
Here real numbers a, b, c and d are parameters such that at least one of a, b, c does not vanish. Some properties of planesMost basic propertiesFor any three points not situated in the same straight line there exists one and only one plane that contains these three points. If two points of a straight line lie in a plane, then every point of the line lies in that plane. If two planes have a common point then they have at least a second point in common. Every plane contains at least three points not lying in the same straight line, and the space contains at least four points not lying in a plane. Further propertiesTwo planes either do not intersect (are parallel), or intersect in a line, or coincide. A line either does not intersect a plane (is parallel to it), or intersects it in a single point, or is contained in the plane. Two lines perpendicular to the same plane are parallel to each other (or coincide). Two planes perpendicular to the same line are parallel to each other (or coincide). Axiomatic approachWhat is wrong with the definitions given above?The definitions given above assume implicitly that the 3-dimensional Euclidean space is already defined, together with (at least one of) such notions as distances, angles, straight lines, Cartesian coordinates, while planes are not defined yet. However, this situation never appears in mathematical theory. In the axiomatic approach points, lines and planes are undefined primitives. The modern approach (below) defines planes in a completely different way. How does it workAxiomatic approach is similar to chess in the following aspect. A chess piece, say a rook, cannot be defined before the whole chess game is defined, since such a phrase as "the rook moves horizontally or vertically, forward or back, through any number of unoccupied squares" makes no sense unless it is already known that "chess is played on a square board of eight rows and eight columns" etc. And conversely, the whole chess game cannot be defined before each piece is defined; the properties of the rook are an indispensable part of the rules of the game. No chess without rooks, no rooks outside chess! One must introduce the game, its pieces and their properties in a single combined definition. Likewise, Euclidean space, its points, lines, planes and their properties are introduced simultaneously in a set of 20 assumptions known as Hilbert's axioms of Euclidean geometry.[1] The "most basic properties of planes" listed above are roughly the plane-related assumptions (Hilbert's axioms), while "further properties" are the first plane-related consequences (theorems). Modern approachThe modern approach defines the three-dimensional Euclidean space more algebraically, via linear spaces and quadratic forms, namely, as a real affine space whose difference space is a three-dimensional inner product space. For further details see Affine space#Euclidean space and space (mathematics). In this approach a plane in an n-dimensional affine space (n ≥ 2) is defined as a (proper or improper) two-dimensional affine subspace. A less formal version of this approach uses points, vectors and scalar product (called also dot product or inner product) of vectors without mentioning linear and affine spaces. Optionally, Cartesian coordinates of points and vectors are used. See algebraic equations below. There, in particular, equivalence between the definition via right angles (orthogonality) and the definition via Cartesian coordinates is explained. Plane geometryPlane geometry (also called "planar geometry") is a part of solid geometry that restricts itself to a single plane ("the plane") treated as a geometric universe. In other words, plane geometry is the theory of the two-dimensional Euclidean space, while solid geometry is the theory of the three-dimensional Euclidean space. Plane geometry studies the properties of plane figures (and configurations). Plane figures in elementary geometry are sets of points, lines, line segments and sometimes curves that fall on the same plane. For example, triangles, polygons and circles. In plane geometry every figure is plane, in contrast to solid geometry. Algebraic equationsIn analytic geometry several closely related algebraic equations are known for a plane in three-dimensional Euclidean space. A few algebraic representations will be discussed. Point-normal representationOne such equation is illustrated in the figure. Point P is an arbitrary point in the plane and O (the origin) is drawn outside the plane. The point A in the plane is chosen such that vector is orthogonal to the plane. The collinear vector is a unit (length 1) vector normal (perpendicular) to the plane which is known as the normal of the plane in point A. Note that d is the distance of O to the plane. The following relation holds for an arbitrary point P in the plane (according to the definition via right angles): This equation for the plane can be rewritten in terms of coordinates with respect to a Cartesian frame with origin in O. Dropping arrows for component vectors (real triplets) that are written bold, we find with and The definition via Cartesian coordinates is thus derived from the definition via right angles. Moreover, the Hesse normal form for the plane (called after the 19th century mathematician Ludwig Otto Hesse) is obtained, it is characterized by the use of a unit-length vector rather than an arbitrary vector orthogonal to the plane. Conversely, the definition via right angles can be derived from the definition via Cartesian coordinates as follows. Given a linear equation for a plane we write It follows that Hence we find the same orthogonality relation, where f , d, and n0 are collinear. The equation may also be written in the following mnemonically convenient form which is the equation for a plane through a point A perpendicular to . Three-point representationThe figure shows a plane that by definition passes through three different points A, B, and C that are not on one line. The point P is an arbitrary point in the plane and the reference point O is again drawn outside the plane, but the case that the plane passes through O is not excluded. Referring to figure 2 we introduce the following definitions Clearly the following two non-collinear vectors belong to the plane Because a plane (an affine space), with a given fixed point as origin is a 2-dimensional linear space and two non-collinear vectors with "tails" in the origin are linearly independent, it follows that any vector in the plane can be written as a linear combination of these two non-collinear vectors. (This is also expressed as: Any vector in the plane can be decomposed into components along the two non-collinear vectors.) In particular, taking A as origin in the plane, The real numbers λ and μ specify the direction of . Hence the following equation for the position vector of the arbitrary point P in the plane: is known as the point-direction representation of the plane. This representation is equal to the three-point representation where , , and are the position vectors of the three points that define the plane. Writing for the position vector of the arbitrary point P in the plane we find that the real triplet (ξ1, ξ2, ξ3) with ξ1 + ξ1 + ξ1 = 1 forms a set of coordinates for P. The numbers {ξ1, ξ2, ξ3 | ξ1+ ξ2+ ξ3 = 1 } are known as the barycentric coordinates of P. It is trivial to go from barycentric coordinates to the "three-point representation", Beyond mathematicsIn industry, a surface plate[2] is a piece of cast iron or other appropriate material whose surface (or rather a part of it) is made as close as possible to a geometric plane (or rather a part of it, usually a square). An old method of their manufacturing is the three-plate method: three roughly flat surfaces become more and more flat when rubbing against each other: first and second; second and third; third and first; first and second again, and so on. It is possible to achieve a surface close to a plane up to 10–5 of its size. Reference
|
Meg Ireland | Milton Beychok; Howard C. Berkowitz | 5
|
Current Winner (to be selected and implemented by an Administrator)
To change, click edit and follow the instructions, or see documentation at {{Featured Article}}.
| The metadata subpage is missing. You can start it via filling in this form or by following the instructions that come up after clicking on the [show] link to the right. | |||
|---|---|---|---|
|
Steam is the vapor (gaseous) phase of water (H2O) usually generated by the boiling of water. When the steam does not contain any liquid water, it is known as dry steam and it is completely colorless. However, when the steam contains tiny droplets of condensed liquid water, it appears to the eye as a white cloud (see the steam being vented from a geothermal power plant in the adjacent photograph).
What is very often referred to as smoke from cooling towers and other vents in industrial facilities is water vapor which has partially condensed and is mistaken to be white smoke. Water aerosols and mists, such as those created by spray cans for misting house plants or certain types of humidifiers, may also create small visible clouds of water droplets, but aerosols, mists and fogs are not steam. Liquids other than water may also form visible clouds when vaporized, but they are not clouds of steam.
Steam is manufactured in industrial processes by the boiling and vaporization of liquid water. It also occurs naturally by being vented from volcanoes, fumaroles, geysers and other geothermal sources.
Steam has a great many industrial and domestic uses. Probably the most important and by far the largest use of steam is in nuclear, fossil fuel and geothermal power plants.
Types of steam
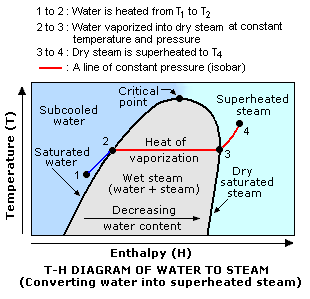
As shown in the adjacent diagram, there are three types of steam:
- Wet steam: A mixture of water plus steam (liquid plus vapor) at the boiling point temperature of water at a given pressure. Quality of steam refers to the fraction or percentage of gaseous steam in a wet steam mixture.
- Dry steam: Steam, at the given pressure, that contains no water (also referred to as saturated steam). The steam quality = 100%. At the top of steam generator units for producing saturated steam, there are moisture separators used to remove residual water droplets from outgoing steam.
- Superheated steam: Dry steam, at the given pressure, that has been heated to a temperature higher than the boiling point of water at that pressure.
Referring to the adjacent drawing again, water is converted into wet, dry saturated or superheated steam in three steps:
- Water at point 1 is heated to its boiling point at the given pressure of point 2 (the dark blue line). At that point the water is then referred to as saturated water. The amount of heat added between points 1 and 2 is called sensible heat.
- The water is further heated at constant pressure (the red isobar from point 2 to point 3) to form wet steam. When it is completely vaporized (at point 3), it is then dry saturated steam. The amount of heat required to completely vaporize the water is called the heat of vaporization and denoted as Hv or Hvap.
- The dry saturated steam is yet further heated at constant pressure (the red isobar from point 3 to point 4). The steam is then referred to as superheated steam. The amount of heat added to superheat the dry saturated steam is also called sensible heat.
- It should be noted that the points 2 and 3 are at the same boiling point temperature and pressure and also that, at those conditions, the liquid and the steam (whether wet or dry) are in equilibrium with each other.
Production
Ways of producing steam from water include use of boilers or steam generators. Boilers are pressure vessels in which water is heated to produce pressurized steam, for generally heating houses or buildings, for steam engines, or a variety of other uses. Steam generators are devices or units, often including boilers (the definitions coincide greatly), for producing (generating) steam for power plant, industrial, or other uses. The size of steam generators ranges from bench top to very large units or sections of a thermal power plant. In the field of nuclear power plants, the term steam generator refers specifically to a particular very large heat exchanger used to thermally connect the primary (reactor plant) system to a secondary (steam plant) system in a pressurized water reactor (PWR) plant, which generates steam for the steam plant, of course.
Uses
Electricity generation
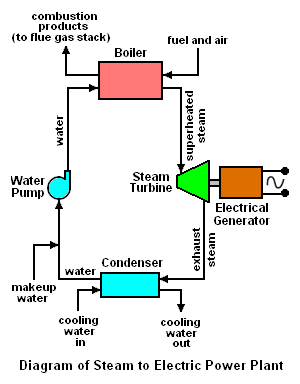
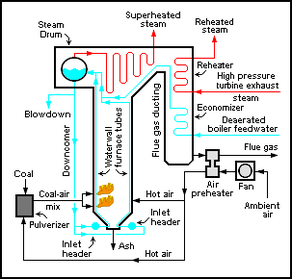
The worldwide capacity of electrical power generation by conventional coal-fired power plants currently amounts to about 800,000 MW[1][2][3][4] and the worldwide capacity of nuclear power generation amounts to about 370,000 MW.[5][6] That amounts to a total of 1,170,000 MW of worldwide generation, most of which involves the use of superheated steam to drive the turbines that spin the electrical generators (see the adjacent schematic diagram).[7]
Assuming an overall thermal efficiency of 34%, a steam generator (boiler) efficiency of 75 to 85% and an electrical generator efficiency of 98.5%, a conventional coal-fired power plant would use superheated steam at a rate of 3.47 to 3.93 (t/h) per MW of power output. Thus, a 1000 MW power plant would use 3,470 to 3,930 metric tons (tonnes) of steam per hour and the steam used by the 1,170,000 MW of worldwide power generation by coal-fired and nuclear power plants might be as much as 4,000,000 to 4,600,000 metric tons of steam per hour.
The diagrams below schematically depict the equipment used in a conventional fuel-fired steam to electric power plant as well as the temperature-entropy (T-S) diagram of the corresponding Rankine cycle. A nuclear power plant differs only to the extent that the heat required by the boiler is provided by heat derived from a nuclear reactor.
Cogeneration of heat and power
Cogeneration is also referred to as combined heat and power or CHP. In electrical power generation, the turbine exhaust steam is typically condensed and returned to the boiler for re-use. However, in one form of cogeneration, all or part of the turbine exhaust steam is distributed through a district heating system to heat buildings rather than being condensed. The world's biggest steam cogeneration system is the district heating system which distributes steam from seven cogeneration plants to provide heating for 100,000 buildings in the city of New York.[8][9]
Steam engines
As an overall definition, a steam engine is an engine that uses steam to perform mechanical work. By that definition, steam turbines are steam engines. However, this section describes steam engines that use the expansion of steam to move a piston that performs work. Such steam engines were the driving force behind the Industrial Revolution of the 18th century and gained widespread commercial use for driving machinery in factories, powering water pumping stations and transport application such as railway locomotives, steamships and road vehicles. The use of tractors driven by steam engines led to an increase in the land available for agricultural cultivation.
Although largely replaced by steam turbines, stationary reciprocating steam engines are still used in industry and elsewhere for driving pumps, gas compressors and other types of machinery.
Uses in industrial process facilities
A great many processes in petroleum refineries, natural gas processing plants, petrochemical plants and other industrial facilities use steam as:
- A heat source in heat exchangers designed to increase the temperature of distillation column feedstocks.
- A heat source for distillation column reboilers.
- A heat source injected directly into various distillation columns known as steam strippers and side-cut strippers to provide the required distillation heat.
- The motive force for steam turbines that are used directly to drive large compressors and centrifugal pumps.
- The motive force for injectors and ejectors.
- A heat source for stripping the spent catalyst in fluid catalytic cracking processes of volatile hydrocarbons.
- A medium for purging of process vessels such as petroleum coke drums in delayed coking units.
- A reactant in catalytic steam-methane reformers for the industrial production of hydrogen.
- A diluent in steam cracking units which produce petrochemical feedstocks such as ethylene and other olefins from natural gas and petroleum hydrocarbons such as methane, ethane, propane, butanes, petroleum naphtha and petroleum gas oil.
- The heat source for evaporation processes in sugar refining and in water desalination processes.
- A heat source flowing through tubular coils installed inside storage tanks to heat certain stored liquids.
Other uses
- Sterilization
- An autoclave, which uses steam under pressure, is used in microbiology laboratories and similar environments for sterilization; autoclaving is also a major method for industrial and home canning of food
- Agricultural
- In agriculture, steam is used for soil sterilization to avoid the use of harmful chemical agents and increase soil health.
- Commercial and domestic uses
- Steam's capability to transfer heat is also used in the home as well as commercial facilities for pressure cookers, steam cleaning of fabrics and carpets, steam ironing and for heating of buildings.
- Ship propulsion
- Steam is sometimes used to power steam turbines to propel naval ships, ice breakers, and other ships; steam turbines are primarily used in nuclear-powered ships, with other new construction using various combinations of gas turbines, diesel engines, and electric motors
Steam tables and Mollier diagrams
Steam tables provide tabulated thermodynamic data for the liquid and vapor phases of water. The table below is only an example of the type of data provided. In a complete set of steam tables, the table would provide data in temperature increments of 1 °C. The complete steam tables would also provide a similar "Saturated Steam:Pressure Table" in which the first column would have pressure values and the second column would be temperature values. Most steam tables include tabulated thermodynamic data for superheated steam as well.
| T °C |
P bar |
P kPa |
ρL kg/m3 |
ρV kg/m3 |
HL J/g |
HVap J/g |
HV J/g |
SL J/(g·K) |
SVap J/(g·K) |
SV J/(g·K) |
|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 0.012282 | 1.2282 | 999.65 | 0.00941 | 42.02 | 2477.2 | 2519.2 | 0.15109 | 8.7487 | 8.8998 |
| 20 | 0.023393 | 2.3393 | 998.19 | 0.01731 | 83.91 | 2453.5 | 2537.4 | 0.29648 | 8.3695 | 8.6660 |
| 30 | 0.042470 | 4.2470 | 995.61 | 0.03042 | 125.73 | 2429.8 | 2555.5 | 0.43675 | 8.0152 | 8.4520 |
| 40 | 0.073849 | 7.3849 | 992.18 | 0.05124 | 167.53 | 2406.0 | 2573.5 | 0.57240 | 7.6831 | 8.2555 |
| 50 | 0.12352 | 12.352 | 988.00 | 0.08315 | 209.34 | 2381.9 | 2591.3 | 0.70381 | 7.3710 | 8.0748 |
| 100 | 1.0142 | 101.42 | 958.35 | 0.5982 | 419.17 | 2256.4 | 2675.6 | 1.3072 | 6.0469 | 7.3541 |
| 150 | 4.7616 | 476.16 | 917.01 | 2.5481 | 632.18 | 2113.7 | 2745.9 | 1.8418 | 4.9953 | 6.8371 |
| 200 | 15.549 | 1554.9 | 864.66 | 7.8610 | 852.27 | 1939.7 | 2792.0 | 2.3305 | 4.0996 | 6.4302 |
| 250 | 39.762 | 3976.2 | 798.89 | 19.967 | 1085.8 | 1715.2 | 2800.9 | 2.7935 | 3.2785 | 6.0721 |
| 300 | 85.879 | 8587.9 | 712.14 | 46.168 | 1345.0 | 1404.6 | 2749.6 | 3.2552 | 2.4507 | 5.7059 |
| Symbols: P = absolute pressure ρL = liquid density ρV = vapor density | ||||||||||
Mollier diagrams are graphical representations of the thermodynamic properties of materials involving "Enthalpy" as one of the coordinates. Mollier diagrams are named after Richard Mollier (1863 - 1935), a professor at Dresden University in Germany, who pioneered the graphical display of the relationship of temperature, pressure, enthalpy, entropy and volume of steam (as well as for moist air) that has aided in the teaching of thermodynamics to many generations of engineers. His enthalpy-entropy (H-S) diagram for steam was first published in 1904.[11][12]
Mollier diagrams are routinely used to visualize the working cycles of thermodynamic systems involved with the chemical engineering process design of power plants (fossil or nuclear), gas compressors, steam turbines, refrigeration systems and air conditioning.
A sample Mollier diagram for steam is presented below and others are available online:[13][14][15]
References
- ↑ A megawatt (MW) of electrical power is often denoted as MWe to differentiate it from other forms of power.
- ↑ International Energy Agency, 2006, Key Energy Statistics (International Energy Agency)
- ↑ International Energy Outlook 2008; Highlights (Energy Information Administration, U.S. DOE)
- ↑ International Energy Outlook 2008: Chapter 5 (Energy Information Administration, U.S. DOE)
- ↑ Energy, Electricity and Nuclear Power Estimates for the Period up to 2030 2009 Edition, International Atomic Energy Agency
- ↑ Nuclear Power Plants, Worldwide European Nuclear Society
- ↑ The amount would be even larger if power plants using other fuels were included (i.e., fuel oil, natural gas and biomass, wood, etc).
- ↑ Steam Carl Bevelhymer, Gotham Gazette, November 10, 2003
- ↑ Newsroom: Steam From the website of the Con Edison company in New York.
- ↑ NISTIR 5078, Thermodynamic Properties of Water Tabulation from the IAPWS Formulation 1995 for the Thermodynamic Properties of Ordinary Water Substance for General and Scientific Use (1998), Allan H. Harvey, National Institute of Standards and Technology
- ↑ Mollier Charts From the website of the ChemicaLogic Corporation
- ↑ R. K. Rajput (2009). Engineering Thermodynamics, 3rd Edition. Jones & Bartlett. ISBN 1-934015-14-8. Google Books Use the search function for "Mollier diagram" and select page 77.
- ↑ Mollier diagram of water-steam From the website of Engineering ToolBox
- ↑ H-S Diagram for Water Associate Professor Israel Urieli, Department of Mechanical Engineering, Ohio University.
- ↑ Mollier Diagram for Water and the excellent animation video at Mollier Diagram for Water
Previous Winners
 Wasan [r]: Classical Japanese mathematics that flourished during the Edo Period from the 17th to mid-19th centuries. [e]
Wasan [r]: Classical Japanese mathematics that flourished during the Edo Period from the 17th to mid-19th centuries. [e] Racism in Australia [r]: The history of racism and restrictive immigration policies in the Commonwealth of Australia. [e]
Racism in Australia [r]: The history of racism and restrictive immigration policies in the Commonwealth of Australia. [e]- Think tank [r]: Add brief definition or description
 Les Paul [r]: (9 June 1915 – 13 August 2009) American innovator, inventor, musician and songwriter, who was notably a pioneer in the development of the solid-body electric guitar. [e]
Les Paul [r]: (9 June 1915 – 13 August 2009) American innovator, inventor, musician and songwriter, who was notably a pioneer in the development of the solid-body electric guitar. [e] Zionism [r]: The ideology that Jews should form a Jewish state in what is traced as the Biblical area of Palestine; there are many interpretations, including the boundaries of such a state and its criteria for citizenship [e] (September 3)
Zionism [r]: The ideology that Jews should form a Jewish state in what is traced as the Biblical area of Palestine; there are many interpretations, including the boundaries of such a state and its criteria for citizenship [e] (September 3) Earth's atmosphere [r]: An envelope of gas that surrounds the Earth and extends from the Earth's surface out thousands of kilometres, becoming increasingly thinner (less dense) with distance but always held in place by Earth's gravitational pull. [e] (August 27)
Earth's atmosphere [r]: An envelope of gas that surrounds the Earth and extends from the Earth's surface out thousands of kilometres, becoming increasingly thinner (less dense) with distance but always held in place by Earth's gravitational pull. [e] (August 27) Joshua Lawrence Chamberlain [r]: U.S. educator deeply bonded to Bowdoin College, from undergraduate to President; American Civil War general and recipient of the Medal of Honor; Governor of Maine [e] (August 20)
Joshua Lawrence Chamberlain [r]: U.S. educator deeply bonded to Bowdoin College, from undergraduate to President; American Civil War general and recipient of the Medal of Honor; Governor of Maine [e] (August 20) The Sporting Life (album) [r]: A 1994 studio album recorded by Diamanda Galás and John Paul Jones. [e] (August 13}
The Sporting Life (album) [r]: A 1994 studio album recorded by Diamanda Galás and John Paul Jones. [e] (August 13} The Rolling Stones [r]: Famous and influential English blues rock group formed in 1962, known for their albums Let It Bleed and Sticky Fingers, and songs '(I Can't Get No) Satisfaction' and 'Start Me Up'. [e] (August 5)
The Rolling Stones [r]: Famous and influential English blues rock group formed in 1962, known for their albums Let It Bleed and Sticky Fingers, and songs '(I Can't Get No) Satisfaction' and 'Start Me Up'. [e] (August 5) Euler angles [r]: three rotation angles that describe any rotation of a 3-dimensional object. [e] (July 30)
Euler angles [r]: three rotation angles that describe any rotation of a 3-dimensional object. [e] (July 30) Chester Nimitz [r]: United States Navy admiral (1885-1966) who was Commander in Chief, Pacific and Pacific Ocean Areas in World War II [e] (July 23)
Chester Nimitz [r]: United States Navy admiral (1885-1966) who was Commander in Chief, Pacific and Pacific Ocean Areas in World War II [e] (July 23) Heat [r]: A form of energy that flows spontaneously from hotter to colder bodies that are in thermal contact. [e] (July 16)
Heat [r]: A form of energy that flows spontaneously from hotter to colder bodies that are in thermal contact. [e] (July 16) Continuum hypothesis [r]: A statement about the size of the continuum, i.e., the number of elements in the set of real numbers. [e] (July 9)
Continuum hypothesis [r]: A statement about the size of the continuum, i.e., the number of elements in the set of real numbers. [e] (July 9) Hawaiian alphabet [r]: The form of writing used in the Hawaiian Language [e] (July 2)
Hawaiian alphabet [r]: The form of writing used in the Hawaiian Language [e] (July 2) Now and Zen [r]: A 1988 studio album recorded by Robert Plant, with guest contributions from Jimmy Page. [e] (June 25)
Now and Zen [r]: A 1988 studio album recorded by Robert Plant, with guest contributions from Jimmy Page. [e] (June 25) Wrench (tool) [r]: A fastening tool used to tighten or loosen threaded fasteners, with one end that makes firm contact with flat surfaces of the fastener, and the other end providing a means of applying force [e] (June 18)
Wrench (tool) [r]: A fastening tool used to tighten or loosen threaded fasteners, with one end that makes firm contact with flat surfaces of the fastener, and the other end providing a means of applying force [e] (June 18) Air preheater [r]: A general term to describe any device designed to preheat the combustion air used in a fuel-burning furnace for the purpose of increasing the thermal efficiency of the furnace. [e] (June 11)
Air preheater [r]: A general term to describe any device designed to preheat the combustion air used in a fuel-burning furnace for the purpose of increasing the thermal efficiency of the furnace. [e] (June 11) 2009 H1N1 influenza virus [r]: A contagious influenza A virus discovered in April 2009, commonly known as swine flu. [e] (June 4)
2009 H1N1 influenza virus [r]: A contagious influenza A virus discovered in April 2009, commonly known as swine flu. [e] (June 4) Gasoline [r]: A fuel for spark-ignited internal combustion engines derived from petroleum crude oil. [e] (21 May)
Gasoline [r]: A fuel for spark-ignited internal combustion engines derived from petroleum crude oil. [e] (21 May) John Brock [r]: Fictional British secret agent who starred in three 1960s thrillers by Desmond Skirrow. [e] (8 May)
John Brock [r]: Fictional British secret agent who starred in three 1960s thrillers by Desmond Skirrow. [e] (8 May) McGuffey Readers [r]: A set of highly influential school textbooks used in the 19th and early 20th centuries in the elementary grades in the United States. [e] (14 Apr)
McGuffey Readers [r]: A set of highly influential school textbooks used in the 19th and early 20th centuries in the elementary grades in the United States. [e] (14 Apr) Vector rotation [r]: Process of rotating one unit vector into a second unit vector. [e] (7 Apr)
Vector rotation [r]: Process of rotating one unit vector into a second unit vector. [e] (7 Apr) Leptin [r]: Hormone secreted by adipocytes that regulates appetite. [e] (31 Mar)
Leptin [r]: Hormone secreted by adipocytes that regulates appetite. [e] (31 Mar) Kansas v. Crane [r]: A 2002 decision of the Supreme Court of the United States, ruling that a person could not be adjudicated a sexual predator and put in indefinite medical confinement, purely on assessment of an emotional disorder, but such action required proof of a likelihood of uncontrollable impulse presenting a clear and present danger. [e] (24 Mar)
Kansas v. Crane [r]: A 2002 decision of the Supreme Court of the United States, ruling that a person could not be adjudicated a sexual predator and put in indefinite medical confinement, purely on assessment of an emotional disorder, but such action required proof of a likelihood of uncontrollable impulse presenting a clear and present danger. [e] (24 Mar) Punch card [r]: A term for cards used for storing information. Herman Hollerith is credited with the invention of the media for storing information from the United States Census of 1890. [e] (17 Mar)
Punch card [r]: A term for cards used for storing information. Herman Hollerith is credited with the invention of the media for storing information from the United States Census of 1890. [e] (17 Mar) Jass–Belote card games [r]: A group of trick-taking card games in which the Jack and Nine of trumps are the highest trumps. [e] (10 Mar)
Jass–Belote card games [r]: A group of trick-taking card games in which the Jack and Nine of trumps are the highest trumps. [e] (10 Mar) Leptotes (orchid) [r]: A genus of orchids formed by nine small species that exist primarily in the dry jungles of South and Southeast Brazil. [e] (3 Mar)
Leptotes (orchid) [r]: A genus of orchids formed by nine small species that exist primarily in the dry jungles of South and Southeast Brazil. [e] (3 Mar) Worm (computers) [r]: Add brief definition or description (24 Feb)
Worm (computers) [r]: Add brief definition or description (24 Feb) Joseph Black [r]: Add brief definition or description (11 Feb 2009)
Joseph Black [r]: Add brief definition or description (11 Feb 2009) Sympathetic magic [r]: Add brief definition or description (17 Jan 2009)
Sympathetic magic [r]: Add brief definition or description (17 Jan 2009) Dien Bien Phu [r]: Add brief definition or description (25 Dec)
Dien Bien Phu [r]: Add brief definition or description (25 Dec)- Blade Runner [r]: Add brief definition or description (25 Nov)
 Piquet [r]: Add brief definition or description (18 Nov)
Piquet [r]: Add brief definition or description (18 Nov) Crash of 2008 [r]: Add brief definition or description (23 Oct)
Crash of 2008 [r]: Add brief definition or description (23 Oct)- Information Management [r]: Add brief definition or description (31 Aug)
 Battle of Gettysburg [r]: Add brief definition or description (8 July)
Battle of Gettysburg [r]: Add brief definition or description (8 July) Drugs banned from the Olympics [r]: Add brief definition or description (1 July)
Drugs banned from the Olympics [r]: Add brief definition or description (1 July) Sea glass [r]: Add brief definition or description (24 June)
Sea glass [r]: Add brief definition or description (24 June) Dazed and Confused (Led Zeppelin song) [r]: Add brief definition or description (17 June)
Dazed and Confused (Led Zeppelin song) [r]: Add brief definition or description (17 June) Hirohito [r]: Add brief definition or description (10 June)
Hirohito [r]: Add brief definition or description (10 June) Henry Kissinger [r]: Add brief definition or description (3 June)
Henry Kissinger [r]: Add brief definition or description (3 June)- Palatalization [r]: Add brief definition or description (27 May)
 Intelligence on the Korean War [r]: Add brief definition or description (20 May)
Intelligence on the Korean War [r]: Add brief definition or description (20 May) Trinity United Church of Christ, Chicago [r]: Add brief definition or description (13 May)
Trinity United Church of Christ, Chicago [r]: Add brief definition or description (13 May) BIOS [r]: Add brief definition or description (6 May)
BIOS [r]: Add brief definition or description (6 May) Miniature Fox Terrier [r]: Add brief definition or description (23 April)
Miniature Fox Terrier [r]: Add brief definition or description (23 April) Joseph II [r]: Add brief definition or description (15 Apr)
Joseph II [r]: Add brief definition or description (15 Apr) British and American English [r]: Add brief definition or description (7 Apr)
British and American English [r]: Add brief definition or description (7 Apr) Count Rumford [r]: Add brief definition or description (1 April)
Count Rumford [r]: Add brief definition or description (1 April) Whale meat [r]: Add brief definition or description (25 March)
Whale meat [r]: Add brief definition or description (25 March) Naval guns [r]: Add brief definition or description (18 March)
Naval guns [r]: Add brief definition or description (18 March) Sri Lanka [r]: Add brief definition or description (11 March)
Sri Lanka [r]: Add brief definition or description (11 March) Led Zeppelin [r]: Add brief definition or description (4 March)
Led Zeppelin [r]: Add brief definition or description (4 March) Martin Luther [r]: Add brief definition or description (20 February)
Martin Luther [r]: Add brief definition or description (20 February) Cosmology [r]: Add brief definition or description (4 February)
Cosmology [r]: Add brief definition or description (4 February) Ernest Rutherford [r]: Add brief definition or description(28 January)
Ernest Rutherford [r]: Add brief definition or description(28 January) Edinburgh [r]: Add brief definition or description (21 January)
Edinburgh [r]: Add brief definition or description (21 January) Russian Revolution of 1905 [r]: Add brief definition or description (8 January 2008)
Russian Revolution of 1905 [r]: Add brief definition or description (8 January 2008) Phosphorus [r]: Add brief definition or description (31 December)
Phosphorus [r]: Add brief definition or description (31 December) John Tyler [r]: Add brief definition or description (6 December)
John Tyler [r]: Add brief definition or description (6 December) Banana [r]: Add brief definition or description (22 November)
Banana [r]: Add brief definition or description (22 November) Augustin-Louis Cauchy [r]: Add brief definition or description (15 November)
Augustin-Louis Cauchy [r]: Add brief definition or description (15 November)- B-17 Flying Fortress (bomber) [r]: Add brief definition or description - 8 November 2007
 Red Sea Urchin [r]: Add brief definition or description - 1 November 2007
Red Sea Urchin [r]: Add brief definition or description - 1 November 2007 Symphony [r]: Add brief definition or description - 25 October 2007
Symphony [r]: Add brief definition or description - 25 October 2007 Oxygen [r]: Add brief definition or description - 18 October 2007
Oxygen [r]: Add brief definition or description - 18 October 2007 Origins and architecture of the Taj Mahal [r]: Add brief definition or description - 11 October 2007
Origins and architecture of the Taj Mahal [r]: Add brief definition or description - 11 October 2007 Fossilization (palaeontology) [r]: Add brief definition or description - 4 October 2007
Fossilization (palaeontology) [r]: Add brief definition or description - 4 October 2007 Cradle of Humankind [r]: Add brief definition or description - 27 September 2007
Cradle of Humankind [r]: Add brief definition or description - 27 September 2007 John Adams [r]: Add brief definition or description - 20 September 2007
John Adams [r]: Add brief definition or description - 20 September 2007 Quakers [r]: Add brief definition or description - 13 September 2007
Quakers [r]: Add brief definition or description - 13 September 2007 Scarborough Castle [r]: Add brief definition or description - 6 September 2007
Scarborough Castle [r]: Add brief definition or description - 6 September 2007 Jane Addams [r]: Add brief definition or description - 30 August 2007
Jane Addams [r]: Add brief definition or description - 30 August 2007 Epidemiology [r]: Add brief definition or description - 23 August 2007
Epidemiology [r]: Add brief definition or description - 23 August 2007 Gay community [r]: Add brief definition or description - 16 August 2007
Gay community [r]: Add brief definition or description - 16 August 2007 Edward I [r]: Add brief definition or description - 9 August 2007
Edward I [r]: Add brief definition or description - 9 August 2007
Rules and Procedure
Rules
- The primary criterion of eligibility for a new draft is that it must have been ranked as a status 1 or 2 (developed or developing), as documented in the History of the article's Metadate template, no more than one month before the date of the next selection (currently every Thursday).
- Any Citizen may nominate a draft.
- No Citizen may have nominated more than one article listed under "current nominees" at a time.
- The article's nominator is indicated simply by the first name in the list of votes (see below).
- At least for now--while the project is still small--you may nominate and vote for drafts of which you are a main author.
- An article can be the New Draft of the Week only once. Nominated articles that have won this honor should be removed from the list and added to the list of previous winners.
- Comments on nominations should be made on the article's talk page.
- Any draft will be deleted when it is past its "last date eligible". Don't worry if this happens to your article; consider nominating it as the Article of the Week.
- If an editor believes that a nominee in his or her area of expertise is ineligible (perhaps due to obvious and embarrassing problems) he or she may remove the draft from consideration. The editor must indicate the reasons why he has done so on the nominated article's talk page.
Nomination
See above section "Add New Nominees Here".
Voting
- To vote, add your name and date in the Supporters column next to an article title, after other supporters for that article, by signing
<br />~~~~. (The date is necessary so that we can determine when the last vote was added.) Your vote is alloted a score of 1. - Add your name in the Specialist supporters column only if you are an editor who is an expert about the topic in question. Your vote is alloted a score of 1 for articles that you created and 2 for articles that you did not create.
- You may vote for as many articles as you wish, and each vote counts separately, but you can only nominate one at a time; see above. You could, theoretically, vote for every nominated article on the page, but this would be pointless.
Ranking
- The list of articles is sorted by number of votes first, then alphabetically.
- Admins should make sure that the votes are correctly tallied, but anyone may do this. Note that "Specialist Votes" are worth 3 points.
Updating
- Each Thursday, one of the admins listed below should move the winning article to the Current Winner section of this page, announce the winner on Citizendium-L and update the "previous winning drafts" section accordingly.
- The winning article will be the article at the top of the list (ie the one with the most votes).
- In the event of two or more having the same number of votes :
- The article with the most specialist supporters is used. Should this fail to produce a winner, the article appearing first by English alphabetical order is used.
- The remaining winning articles are guaranteed this position in the following weeks, again in alphabetical order. No further voting should take place on these, which remain at the top of the table with notices to that effect. Further nominations and voting take place to determine future winning articles for the following weeks.
- Winning articles may be named New Draft of the Week beyond their last eligible date if their circumstances are so described above.
- The article with the most specialist supporters is used. Should this fail to produce a winner, the article appearing first by English alphabetical order is used.
Administrators
The Administrators of this program are the same as the admins for CZ:Article of the Week.
References
See Also
- CZ:Article of the Week
- CZ:Markup tags for partial transclusion of selected text in an article
- CZ:Monthly Write-a-Thon
| Citizendium Initiatives | ||
|---|---|---|
| Eduzendium | Featured Article | Recruitment | Subpages | Core Articles | Uncategorized pages | Requested Articles | Feedback Requests | Wanted Articles |
|width=10% align=center style="background:#F5F5F5"| |}