Note (music)

In music, a note is an abstract representation of the pitch and duration of a tone. The pitch designated by a note is objective only in the case of a simple tone (also called a pure tone) such as produced by a tuning fork, which consists of only a single frequency of vibration, in which case the pitch is uniquely related to that frequency at a given loudness.

(PD) Image: John R. Brews
Frequencies of various pure tones. The various A-notes are a factor of two apart in frequency, and span an octave (eight notes). The MIDI pitch numbers are explained later.

(PD) Image: John R. Brews
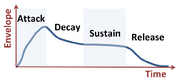
The amplitude of a musical note varies in time according to its sound envelope.

A musical instrument on the other hand, produces a tone, which is a superposition of various frequencies with various amplitudes and phases peculiar to the instrument, and also affected by the manner of play that determines the sound envelope of the note (referred to by Lamb below as "adventitious circumstances"). A laboratory determination of pitch is made by a subject listening to a tone from a musical instrument and to a simple tone, such as that produced by a tuning fork, and identifying circumstances where the instrument and the simple tone sound alike. As a result, for other than simple tones, pitch is not a purely objective physical property; it is a subjective psychoacoustical attribute of a sound.

To quote Lamb:

One musical note may differ from another in respect of pitch, quality, and loudness. The pitch is usually estimated as that of the first simple-harmonic vibration in the series, viz. that of lowest frequency, but if the amplitude of this first component be relatively small, and especially if it fall near the lower limit of the audible scale, the estimated pitch may be that of the second component. By "quality" is meant that unmistakable character which distinguishes a note on one instrument from the note of same pitch as given by another...difference of quality, so far as it is not due to adventitious circumstances,† can only be ascribed to differences of vibration-form, and so to differences in the relative amplitude and phases of the simple-harmonic constituents. †Such as the manner in which the sound sets in and ceases; this is different for instance in the violin and the piano.

What Lamb refers to as "quality" of a tone also is referred to as timbre.

Notation

(PD) Image: John R. Brews
Musical clefs and notes of various durations arranged on the grand staff of eleven lines.

In Western musical notation, the pitch of a sound is indicated by the vertical position of the symbol for the note on a staff or stave, an array of parallel leger lines (from the French leger=light), as shown in the figure. Certain lines on the staff are identified by clefs. The upper clef is called the treble or G-clef, and the lower clef is called the bass or F-clef.

The names of the notes correspond to the first seven letters of the alphabet, applied to both lines and spaces. The labeling associated with the lines on the staff is indicated, and the labels for the spaces follow alphabetically. Men's voices are considered to range from lower G on the bass staff (the bottom five lines), through the next G in the tenor staff, to to the third G in the in the alto staff. Women's and boy's voices range an octave higher, running up to the next G in the treble staff. See Jones, §24, p.9. For voice exercises, the first note C on the so-called natural scale or scale of C is called doh and the notes of the first octave are named by the syllables doh, ray, me, fah, soh, lah, te, doh.

The absolute pitch denoted by a position on the staff is set by the key of the musical piece. Pure tones separated by an octave on the staff (that is, a combination of eight lines and spaces on the staff) are a factor of two different in frequency. A pitch between C and D, say, is called C-sharp (denoted C^#) and is a semitone above C, or labeled D-flat (denoted D^♭), a semitone below D.

The right-to-left position of the notes indicate the order in which they are played, the further to the right the later, with notes directly above one another played simultaneously.

Duration of a note is indicated by its symbol. Examples are shown in the figure, with the longest or whole note at the bottom, and the two half notes above it that combine to the same duration. The quarter note, eighth notes and sixteenth notes are successively stacked above.

The relative duration of a whole note is established by dividing the horizontal length of the staff into measures, bounded by vertical bars, and a time signature that determines how many "beats" occur in a measure, and which note corresponds to a beat. For example, a ¾ time signature means three beats to a measure and a quarter note gets one beat, a half-note two beats, a whole note four beats, and so forth. Musical notation does not assign absolute duration to a beat. Tempo indications, like presto and allegro, provide further guidance for pace.

Digital representation of notes

A Musical Instrument Digital Interface or MIDI file is the digital equivalent of sheet music. In this system, each note is assigned a numeric value with A440 (the A above middle C) given the number 69. The general formula for finding the frequency f of the pure tone associated with the pitch corresponding to a MIDI number n (an integer between 1 and 128 = 2⁷) is:

$f=440\times 2^{\left((n-69)/12\right)}\ ,$

which inverts to provide MIDI pitch number as:

$n=12\log _{2}\left({\frac {f}{440}}\right)+69\ ,$

which is meaningful only for frequencies resulting in integer values of n in the range 1 - 128. Here log₂ is the logarithm of its argument to the base 2. With these formulas, middle C with MIDI number 60 is assigned the frequency 261.6256... Hz.

There are 128 = 2⁷ numbers available for digital assignment, many more than the 88 keys of a piano, so many more pitches are possible. The grand piano keyboard corresponds to MIDI numbers 21 - 108 or 27.5 Hz - 4,186 Hz.

The MIDI protocol sends messages that include aspects of pitch, timbre, and timing that allow a music synthesizer to imitate a piece of music played upon one instrument, or even several different instruments, in a predictable fashion. Instructions designated Note-On and Note-Off specify the duration, loudness and pitch of a note. The timbre of a tone is selected by a MIDI patch number, with patch 20 a church organ and 106 a banjo, for example.