Envelope function

© Image: John R. Brews
Top and bottom envelope functions for a modulated sine wave.

See also: Modulation

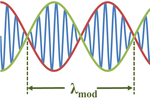
In physics and engineering, the envelope function of a rapidly varying signal is a smooth curve outlining its extremes in amplitude. The figure illustrates a sine wave varying between an upper and a lower envelope. The envelope function may be a function of time, or of space, or indeed of any variable.

Example: Beating waves

See also: Beat (acoustics)

(PD) Image: John R. Brews
A modulated wave resulting from adding two sine waves of nearly identical wavelength and frequency.

A common situation resulting in an envelope function in both space x and time t is the superposition of two waves of almost the same wavelength and frequency:

$F(x,\ t)=\sin \left[2\pi \left({\frac {x}{\lambda -\Delta \lambda }}-(f+\Delta f)t\right)\right]$$+\sin \left[2\pi \left({\frac {x}{\lambda +\Delta \lambda }}-(f-\Delta f)t\right)\right]$

$\approx 2\cos \left[2\pi \left({\frac {x}{\lambda _{mod}}}-\Delta f\ t\right)\right]\ \sin \left[2\pi \left({\frac {x}{\lambda }}-f\ t\right)\right]\ ,$

which uses the trigonometric formula for the addition of two sine waves, and the approximation Δλ<<λ:

${\frac {1}{\lambda \pm \Delta \lambda }}={\frac {1}{\lambda }}\ {\frac {1}{1\pm \Delta \lambda /\lambda }}\approx {\frac {1}{\lambda }}\mp {\frac {\Delta \lambda }{\lambda ^{2}}}.$

Here the modulation wavelength λ_mod is given by:

$\lambda _{mod}={\frac {\lambda ^{2}}{\Delta \lambda }}\ .$

The modulation wavelength is double that of the envelope itself because each half-wavelength of the modulating cosine wave governs both positive and negative values of the modulated sine wave.

If this wave is a sound wave, the ear hears the frequency associated with f and the amplitude of this sound varies with the beat frequency Δf.

Phase and group velocity

The argument of the sinusoids above apart from a factor 2π are:

$\xi _{c}=\left({\frac {x}{\lambda }}-f\ t\right)\ ,$

$\xi _{e}=\left({\frac {x}{\lambda _{mod}}}-\Delta f\ t\right)\ ,$

with subscripts c and e referring to the carrier and the envelope. The same values for these functions occur when these arguments increase by unity, whether that increase is a result of an increase in distance x or an increase in time t. That is, the same amplitude results for the same value of ξ_c and ξ_b, even though this value results for different choices of x and t. This invariance means that one can trace these waveforms in space to find how a position of fixed amplitude propagates in time with a speed that keeps ξ fixed; that is, for the carrier:

$\left({\frac {x}{\lambda }}-f\ t\right)=\left({\frac {x+\Delta x}{\lambda }}-f(t+\Delta t)\right)\ ,$

which determines for a constant amplitude the distance Δx is related to the time interval Δt by the so-called phase velocity v_p

$v_{p}={\frac {\Delta x}{\Delta t}}=\lambda f\ .$

On the other hand, the same considerations show the envelope propagates at the so-called group velocity v_g:

$v_{g}={\frac {\Delta x}{\Delta t}}=\lambda _{mod}\Delta f=\lambda ^{2}{\frac {\Delta f}{\Delta \lambda }}\ .$

A more common expression for the group velocity is obtained by introducing the wavevector k:

$k={\frac {2\pi }{\lambda }}\ .$

We notice that for small changes Δλ, the magnitude of the corresponding small change in wavevector:

$\Delta k=\left|{\frac {dk}{d\lambda }}\right|=2\pi {\frac {\Delta \lambda }{\lambda ^{2}}}\ ,$

so the group velocity can be rewritten as:

$v_{g}={\frac {2\pi \Delta f}{\Delta k}}\ .$

In all media, frequency and wavevector are related by a dispersion relation, 2πf ≡ ω = ω(k), and the group velocity can be written:

$v_{g}={\frac {d\omega (k)}{dk}}\ .$

Here ω is the frequency in radians/s. In a medium such as classical vacuum the dispersion relation for electromagnetic waves is:

$\omega =c_{0}k$

where c₀ is the speed of light in classical vacuum. For this case, the phase and group velocities both are c₀. In so-called dispersive media the dispersion relation can be a complicated function of wavevector, and the phase and group velocities are not the same. In more than one dimension, the phase and group velocities may have different directions.