Two-port network: Difference between revisions
imported>John R. Brews (notation) |
imported>John R. Brews m (nowrap) |
||
| Line 2: | Line 2: | ||
{{TOC|right}} | {{TOC|right}} | ||
{{Image|Two-port with Thevenin driver.PNG|right|350px| Two-port network with symbol definitions. A [[Thevenin voltage source]] with [[Thevenin impedance]] ''Z<sub>Th</sub>'' drives port 1, and impedance ''Z<sub>L</sub>'' loads port 2}} | {{Image|Two-port with Thevenin driver.PNG|right|350px| Two-port network with symbol definitions. A [[Thevenin voltage source]] with [[Thevenin impedance]] ''Z<sub>Th</sub>'' drives {{nowrap|port 1,}} and impedance ''Z<sub>L</sub>'' loads {{nowrap|port 2}}}} | ||
A '''two-port network''' is an [[electrical circuit]] with two ''pairs'' of terminals. As shown in the figure, two terminals constitute a '''port''' ''only'' if they satisfy the essential requirement known as the '''port condition''', namely, the same current must enter and leave a port.<ref name=Gray/><ref name=Jaeger/> | A '''two-port network''' is an [[electrical circuit]] with two ''pairs'' of terminals. As shown in the figure, two terminals constitute a '''port''' ''only'' if they satisfy the essential requirement known as the '''port condition''', namely, the same current must enter and leave a port.<ref name=Gray/><ref name=Jaeger/> | ||
Examples include small-signal models for transistors (such as the [[hybrid-pi model]]), [[electronic filter|filter]]s and [[matching network]]s. The analysis of passive two-port networks is an outgrowth of reciprocity theorems first derived by Lorentz.<ref name=Jasper/> | Examples include small-signal models for transistors (such as the [[hybrid-pi model]]), [[electronic filter|filter]]s and [[matching network]]s. The analysis of passive two-port networks is an outgrowth of reciprocity theorems first derived by Lorentz.<ref name=Jasper/> | ||
| Line 8: | Line 8: | ||
A two-port network makes possible the replacement of either a complete circuit or part of it by a "[[black box]]" with a only four distinct parameters, enabling us to separate its behavior from that of its internal constituents, thus simplifying analysis. Any linear circuit with four terminals can be transformed into a two-port network provided that it does not contain an independent source and satisfies the port conditions. | A two-port network makes possible the replacement of either a complete circuit or part of it by a "[[black box]]" with a only four distinct parameters, enabling us to separate its behavior from that of its internal constituents, thus simplifying analysis. Any linear circuit with four terminals can be transformed into a two-port network provided that it does not contain an independent source and satisfies the port conditions. | ||
The parameters used to describe a two-port network are the following: z, y, h, g. Each choice corresponds to a different choice for which pair of variables from port 1 and port 2 are chosen to be independent, externally applied sources and which two will be the dependent resultant variables determine by the two-port parameters (see the figure). The port currents and voltages are denoted as follows: | The parameters used to describe a two-port network are the following: z, y, h, g. Each choice corresponds to a different choice for which pair of variables from {{nowrap|port 1}} and {{nowrap|port 2}} are chosen to be independent, externally applied sources and which two will be the dependent resultant variables determine by the two-port parameters (see the figure). The port currents and voltages are denoted as follows: | ||
:<math>{V_1}</math> = Port 1 voltage | :<math>{V_1}</math> = Port 1 voltage | ||
:<math>{I_1}</math> = Port 1 current | :<math>{I_1}</math> = Port 1 current | ||
| Line 61: | Line 61: | ||
:<math>r_E=\frac{r_\pi}{\beta+1} \ , </math> | :<math>r_E=\frac{r_\pi}{\beta+1} \ , </math> | ||
and | and the notation '//' indicates the resistance of resistors in parallel: | ||
:<math> R_1\text{//}R_2 = \left(\frac{1}{R_1} + \frac{1}{R_2} \right)^{-1} \ . </math> | :<math> R_1\text{//}R_2 = \left(\frac{1}{R_1} + \frac{1}{R_2} \right)^{-1} \ . </math> | ||
| Line 88: | Line 84: | ||
==Hybrid parameters (h-parameters) == | ==Hybrid parameters (h-parameters) == | ||
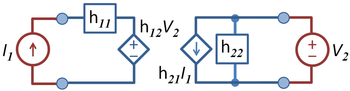
{{Image|H-equivalent two-port.PNG|right|350px|H-equivalent two-port showing independent variables ''I<sub>1</sub>'' and ''V<sub>2</sub>''.}} | {{Image|H-equivalent two-port.PNG|right|350px|H-equivalent two-port showing independent variables ''I<sub>1</sub>'' and ''V<sub>2</sub>''.}} | ||
The figure shows the two-port driven by two external sources, a current source at port 1 and a voltage source at port 2, making the input current ''I<sub>1</sub>'' and input voltage ''V<sub>2</sub>'' the independent variables controlled from outside the two-port. The voltage at port 1, ''V<sub>1</sub>'', and the current at port 2, ''I<sub>2</sub>'', are determined in terms of these inputs by the ''h''-parameters defined by: | The figure shows the two-port driven by two external sources, a current source at {{nowrap|port 1}} and a voltage source at {{nowrap|port 2,}} making the input current ''I<sub>1</sub>'' and input voltage ''V<sub>2</sub>'' the independent variables controlled from outside the two-port. The voltage at {{nowrap|port 1,}} ''V<sub>1</sub>'', and the current at {{nowrap|port 2,}} ''I<sub>2</sub>'', are determined in terms of these inputs by the ''h''-parameters defined by: | ||
:<math> {V_1 \choose I_2} = \begin{pmatrix} h_{11} & h_{12} \\ h_{21} & h_{22} \end{pmatrix}{I_1 \choose V_2} </math>. | :<math> {V_1 \choose I_2} = \begin{pmatrix} h_{11} & h_{12} \\ h_{21} & h_{22} \end{pmatrix}{I_1 \choose V_2} </math>. | ||
| Line 97: | Line 93: | ||
:<math>h_{21} = {I_2 \over I_1 } \bigg|_{V_2 = 0} \qquad h_{22} = {I_2 \over V_2 } \bigg|_{I_1 = 0}</math> | :<math>h_{21} = {I_2 \over I_1 } \bigg|_{V_2 = 0} \qquad h_{22} = {I_2 \over V_2 } \bigg|_{I_1 = 0}</math> | ||
Often this circuit is selected when a current amplifier is described, because the port 1 input is the independent input current and port 2 output is the dependent current. | Often this circuit is selected when a current amplifier is described, because the {{nowrap|port 1}} input is the independent input current and {{nowrap|port 2}} output is the dependent current. | ||
Notice that off-diagonal h-parameters are dimensionless, while the series-connected diagonal element has dimensions of ohms, while the shunt-connected diagonal element has dimensions of siemens. | Notice that off-diagonal h-parameters are dimensionless, while the series-connected diagonal element has dimensions of ohms, while the shunt-connected diagonal element has dimensions of siemens. | ||
| Line 133: | Line 129: | ||
|<math>\ \begin{matrix} \frac {r_E} {r_O} \end{matrix} \ </math> << 1 | |<math>\ \begin{matrix} \frac {r_E} {r_O} \end{matrix} \ </math> << 1 | ||
|} | |} | ||
The transistor β is related to the transistor transconductance ''g<sub>m</sub>'' as: | |||
:<math> \beta=g_m r_\pi \ . </math> | |||
==Inverse hybrid parameters (g-parameters)== | ==Inverse hybrid parameters (g-parameters)== | ||
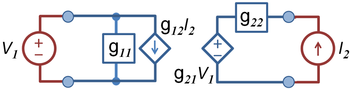
{{Image|G-equivalent two-port.PNG|right|350px| G-equivalent two-port showing independent variables ''V<sub>1</sub>'' and ''I<sub>2</sub>''.}} | {{Image|G-equivalent two-port.PNG|right|350px| G-equivalent two-port showing independent variables ''V<sub>1</sub>'' and ''I<sub>2</sub>''.}} | ||
The figure shows the two-port driven by two external sources, a voltage source at port 1 and a current source at port 2, making the input voltage ''V<sub>1</sub>'' and input current ''I<sub>2</sub>'' the independent variables controlled from outside the two-port. The current at port 1, ''I<sub>1</sub>'', and the voltage at port 2, ''V<sub>2</sub>'', are determined in terms of these inputs by the ''g''-parameters defined by: | The figure shows the two-port driven by two external sources, a voltage source at {{nowrap|port 1}} and a current source at {{nowrap|port 2,}} making the input voltage ''V<sub>1</sub>'' and input current ''I<sub>2</sub>'' the independent variables controlled from outside the two-port. The current at {{nowrap|port 1,}} ''I<sub>1</sub>'', and the voltage at {{nowrap|port 2,}} ''V<sub>2</sub>'', are determined in terms of these inputs by the ''g''-parameters defined by: | ||
:<math> {I_1 \choose V_2} = \begin{pmatrix} g_{11} & g_{12} \\ g_{21} & g_{22} \end{pmatrix}{V_1 \choose I_2} </math>. | :<math> {I_1 \choose V_2} = \begin{pmatrix} g_{11} & g_{12} \\ g_{21} & g_{22} \end{pmatrix}{V_1 \choose I_2} </math>. | ||
| Line 148: | Line 146: | ||
Often this circuit is selected to describe a voltage amplifier, as the port 1 input is an independent voltage, and the port 2 output is a dependent voltage. Notice that off-diagonal g-parameters are dimensionless, while the series-connected diagonal element has dimensions of ohms, while the shunt-connected diagonal element has dimensions of siemens. | Often this circuit is selected to describe a voltage amplifier, as the {{nowrap|port 1}} input is an independent voltage, and the {{nowrap|port 2}} output is a dependent voltage. Notice that off-diagonal g-parameters are dimensionless, while the series-connected diagonal element has dimensions of ohms, while the shunt-connected diagonal element has dimensions of siemens. | ||
===Example: common base amplifier=== | ===Example: common base amplifier=== | ||
Revision as of 00:50, 21 May 2011

Two-port network with symbol definitions. A Thevenin voltage source with Thevenin impedance ZTh drives port 1, and impedance ZL loads port 2
A two-port network is an electrical circuit with two pairs of terminals. As shown in the figure, two terminals constitute a port only if they satisfy the essential requirement known as the port condition, namely, the same current must enter and leave a port.[1][2] Examples include small-signal models for transistors (such as the hybrid-pi model), filters and matching networks. The analysis of passive two-port networks is an outgrowth of reciprocity theorems first derived by Lorentz.[3]
A two-port network makes possible the replacement of either a complete circuit or part of it by a "black box" with a only four distinct parameters, enabling us to separate its behavior from that of its internal constituents, thus simplifying analysis. Any linear circuit with four terminals can be transformed into a two-port network provided that it does not contain an independent source and satisfies the port conditions.
The parameters used to describe a two-port network are the following: z, y, h, g. Each choice corresponds to a different choice for which pair of variables from port 1 and port 2 are chosen to be independent, externally applied sources and which two will be the dependent resultant variables determine by the two-port parameters (see the figure). The port currents and voltages are denoted as follows:
- = Port 1 voltage
- = Port 1 current
- = Port 2 voltage
- = Port 2 current
The relations between inputs and outputs usually are expressed in matrix notation.
These variables are most useful at low to moderate frequencies. At high frequencies (for example, microwave frequencies) power and energy are more useful variables, and the two-port approach based on current and voltages that is discussed here is replaced by an approach based upon scattering parameters.[4]
Though some authors use the terms two-port network and four-terminal network interchangeably, the latter represents a more general concept. Not all four-terminal networks are two-port networks. A pair of terminals can be called a port only if the current entering one is equal to the current leaving the other (the port condition). Only those four-terminal networks in which the four terminals can be paired into two ports can be called two-ports.[1][2]
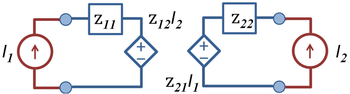
Impedance parameters (z-parameters)
The figure shows the two-port driven by two external current sources, making the input currents I1 and I2 the independent variables controlled from outside the two-port. The port voltages are determined in terms of these input currents by the z-parameters defined by:
- .
Notice that all the series connected elements represented by z-parameters have dimensions of ohms, as do the dependent source parameters.
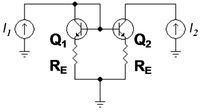
Example: bipolar current mirror with emitter degeneration
The figure at left shows a bipolar current mirror with emitter resistors to increase its output resistance.[5] Transistor Q1 is diode connected, which is to say its collector-base voltage is zero. The figure at right shows the small-signal circuit equivalent to the transistor circuit. Transistor Q1 is represented by its emitter resistance rE ≈ VT / IE (VT = thermal voltage, IE = Q-point emitter current), a simplification made possible because the dependent current source in the hybrid-pi model for Q1 draws the same current as a resistor 1 / gm connected across rπ. The second transistor Q2 is represented by its hybrid-pi model. Table 1 below shows the z-parameter expressions that make the z-equivalent two-port electrically equivalent to the small-signal circuit for the mirror.
| Table 1 | Expression | Approximation |
|---|---|---|
In this table, the bipolar transistor emitter resistance denoted rE is defined as:
and the notation '//' indicates the resistance of resistors in parallel:
The negative feedback introduced by resistors RE can be seen in these parameters. For example, when used as an active load in a differential amplifier, I1 ≈ -I2, making the output impedance of the mirror approximately R22 -R21 ≈ 2 β rORE /( rπ+2RE ) compared to only rO without feedback (that is with RE = 0 Ω) . At the same time, the impedance on the reference side of the mirror is approximately R11 -R12 ≈ , only a moderate value, but still larger than rE with no feedback. In the differential amplifier application, a large output resistance increases the difference-mode gain, a good thing, and a small mirror input resistance is desirable to avoid Miller effect.
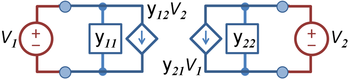
Admittance parameters (y-parameters)
The figure shows the two-port driven by two external voltage sources, making the input voltages V1 and V2 the independent variables controlled from outside the two-port. The port currents are determined in terms of these input voltages by the y-parameters defined by:
- .
where
The network is said to be reciprocal if . Notice that all the shunt-connected elements are represented by y-parameters with dimensions of siemens, as are the dependent source parameters.
Hybrid parameters (h-parameters)
The figure shows the two-port driven by two external sources, a current source at port 1 and a voltage source at port 2, making the input current I1 and input voltage V2 the independent variables controlled from outside the two-port. The voltage at port 1, V1, and the current at port 2, I2, are determined in terms of these inputs by the h-parameters defined by:
- .
where
Often this circuit is selected when a current amplifier is described, because the port 1 input is the independent input current and port 2 output is the dependent current.
Notice that off-diagonal h-parameters are dimensionless, while the series-connected diagonal element has dimensions of ohms, while the shunt-connected diagonal element has dimensions of siemens.
Example: common base amplifier
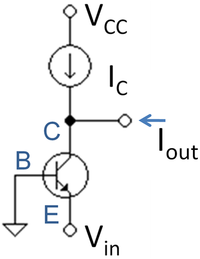
The common base amplifier is shown at left. The current source in the collector lead is an ideal DC source, and as such will not allow passage of any varying signal through itself. Its purpose in the circuit is to provide a DC bias current that sets the operating point (the quiescent transistor state about which the transistor varies in processing the signal). A signal current is applied to the emitter, and an output voltage is required at the collector. The output node is shown as an open circuit (no load) at the left, but to make use of the amplifier, a load can be attached, which then will draw a signal current from the collector node.
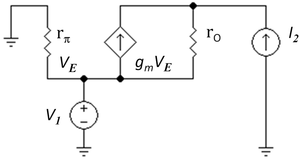
The small-signal circuit at the right assumes the voltage at the collector is a specified variable, and the output current is to be determined. The input current at the emitter also is a specified variable, and the signal voltage VE developed at the emitter is a dependent variable.
Tabulated formulas in Table 2 make the h-equivalent circuit of the transistor agree with the small-signal low-frequency circuit found using the transistor hybrid-pi model at the right. Notation: rπ = base resistance of transistor, rO = output resistance, and gm = transconductance. The negative sign for h21 reflects the convention that I1, I2 are positive when directed into the two-port. Parameter h21 represents the current gain of the circuit viewed as a current amplifier. A non-zero value for h12 means the output voltage affects the input voltage, that is, this amplifier is bilateral. If h12 = 0, the amplifier is unilateral.
| Table 2 | Expression | Approximation |
|---|---|---|
| << 1 |
The transistor β is related to the transistor transconductance gm as:
Inverse hybrid parameters (g-parameters)
The figure shows the two-port driven by two external sources, a voltage source at port 1 and a current source at port 2, making the input voltage V1 and input current I2 the independent variables controlled from outside the two-port. The current at port 1, I1, and the voltage at port 2, V2, are determined in terms of these inputs by the g-parameters defined by:
- .
where
Often this circuit is selected to describe a voltage amplifier, as the port 1 input is an independent voltage, and the port 2 output is a dependent voltage. Notice that off-diagonal g-parameters are dimensionless, while the series-connected diagonal element has dimensions of ohms, while the shunt-connected diagonal element has dimensions of siemens.
Example: common base amplifier
The common base amplifier is shown again at the left. This time, a signal voltage is applied to the emitter, and an output current is taken from the collector.
The small-signal circuit at the right assumes the current at the collector is a specified variable, and the output voltage is to be determined. The input voltage at the emitter also is a specified variable, and the signal current driven into the emitter is a dependent variable.
The tabulated formulas in Table 3 make the g-equivalent two-port for the amplifier agree with the small-signal circuit found using the small-signal low-frequency hybrid-pi model for the transistor. Notation: rπ = base resistance of transistor, rO = output resistance, and gm = transconductance. Parameter g21 represents the voltage gain of this circuit viewed as a voltage amplifier. The negative sign for g12 reflects the convention that I1, I2 are positive when directed into the two-port. A non-zero value for g12 means the output current affects the input current, that is, this amplifier is bilateral. If g12 = 0, the amplifier is unilateral.
| Table 3 | Expression |
|---|---|
References
- ↑ 1.0 1.1 P.R. Gray, P.J. Hurst, S.H. Lewis, and R.G. Meyer (2001). Analysis and Design of Analog Integrated Circuits, Fourth Edition. New York: Wiley, §3.2, p. 172. ISBN 0471321680.
- ↑ 2.0 2.1 R. C. Jaeger and T. N. Blalock (2006). Microelectronic Circuit Design, Third Edition. Boston: McGraw-Hill, §10.5 §13.5 §13.8. ISBN 9780073191638.
- ↑ See review by Jasper J. Goedbloed (2003). Reciprocity and EMC measurements. Presentation at 2003 EMC Zurich Symposium and as IEEE EMC EMCS Newsletter pp.93-104.
- ↑ David M. Pozar (2005). “Chapter 4: Microwave network analysis”, Microwave Engineering, 3rd Edition. John Wiley & Sons, pp. 161-221. ISBN 047164451X (Softcover).
- ↑ The emitter-leg resistors counteract any current increase by decreasing the transistor VBE. That is, the resistors RE cause negative feedback that opposes change in current. In particular, any change in output voltage results in less change in current than without this feedback, which means the output resistance of the mirror has increased.




![{\displaystyle \left[{\begin{array}{c}V_{1}\\V_{2}\end{array}}\right]=\left[{\begin{array}{cc}z_{11}&z_{12}\\z_{21}&z_{22}\end{array}}\right]\left[{\begin{array}{c}I_{1}\\I_{2}\end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7645f82f97b057892f6d77d80bbf01b985aaae0f)

























![{\displaystyle \left[{\begin{array}{c}I_{1}\\I_{2}\end{array}}\right]=\left[{\begin{array}{cc}y_{11}&y_{12}\\y_{21}&y_{22}\end{array}}\right]\left[{\begin{array}{c}V_{1}\\V_{2}\end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f0a34623af2771a0510c92e6a21ac4e6de760aa)