Envelope function

© Image: John R. Brews
Top and bottom envelope functions for a modulated sine wave.

See also: Modulation

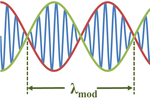
In physics and engineering, the envelope function of a rapidly varying signal is a smooth curve outlining its extremes in amplitude. The figure illustrates a sine wave varying between an upper and a lower envelope. The envelope function may be a function of time, or of space, or indeed of any variable.

Example: Beating waves

See also: Beat (acoustics)

(PD) Image: John R. Brews
A modulated wave resulting from adding two sine waves of nearly identical wavelength and frequency.

A common situation resulting in an envelope function in both space x and time t is the superposition of two waves of almost the same wavelength and frequency:

$F(x,\ t)=\sin \left[2\pi \left({\frac {x}{\lambda -\Delta \lambda }}-(f+\Delta f)t\right)\right]$$+\sin \left[2\pi \left({\frac {x}{\lambda +\Delta \lambda }}-(f-\Delta f)t\right)\right]$

$\approx 2\cos \left[2\pi \left({\frac {x}{\lambda _{mod}}}-\Delta f\ t\right)\right]\ \sin \left[2\pi \left({\frac {x}{\lambda }}-f\ t\right)\right]\ ,$

which uses the trigonometric formula for the addition of two sine waves, and the approximation Δλ<<λ:

${\frac {1}{\lambda \pm \Delta \lambda }}={\frac {1}{\lambda }}\ {\frac {1}{1\pm \Delta \lambda /\lambda }}\approx {\frac {1}{\lambda }}\mp {\frac {\Delta \lambda }{\lambda ^{2}}}.$

Here the modulation wavelength λ_mod is given by:

$\lambda _{mod}={\frac {\lambda ^{2}}{\Delta \lambda }}\ .$

The modulation wavelength is double that of the envelope itself because each half-wavelength of the modulating cosine wave governs both positive and negative values of the modulated sine wave.

If this wave is a sound wave, the ear hears the frequency associated with f and the amplitude of this sound varies with the beat frequency Δf.

Phase and group velocity

The argument of the sinusoids above apart from a factor 2π are:

$\xi _{c}=\left({\frac {x}{\lambda }}-f\ t\right)\ ,$

$\xi _{e}=\left({\frac {x}{\lambda _{mod}}}-\Delta f\ t\right)\ ,$

with subscripts c and e referring to the carrier and the envelope. The same amplitude F of the wave results for the same value of ξ_c and ξ_b, even though this value results for different choices of x and t. This invariance means that one can trace these waveforms in space to find how a position of fixed amplitude propagates in time with a speed that keeps ξ fixed; that is, for the carrier:

$\left({\frac {x}{\lambda }}-f\ t\right)=\left({\frac {x+\Delta x}{\lambda }}-f(t+\Delta t)\right)\ ,$

which determines for a constant amplitude the distance Δx is related to the time interval Δt by the so-called phase velocity v_p

$v_{p}={\frac {\Delta x}{\Delta t}}=\lambda f\ .$

On the other hand, the same considerations show the envelope propagates at the so-called group velocity v_g:

$v_{g}={\frac {\Delta x}{\Delta t}}=\lambda _{mod}\Delta f=\lambda ^{2}{\frac {\Delta f}{\Delta \lambda }}\ .$

A more common expression for the group velocity is obtained by introducing the wavevector k:

$k={\frac {2\pi }{\lambda }}\ .$

We notice that for small changes Δλ, the magnitude of the corresponding small change in wavevector:

$\Delta k=\left|{\frac {dk}{d\lambda }}\right|=2\pi {\frac {\Delta \lambda }{\lambda ^{2}}}\ ,$

so the group velocity can be rewritten as:

$v_{g}={\frac {2\pi \Delta f}{\Delta k}}\ .$

In all media, frequency and wavevector are related by a dispersion relation, 2πf ≡ ω = ω(k), and the group velocity can be written:

$v_{g}={\frac {d\omega (k)}{dk}}\ .$

Here ω is the frequency in radians/s. In a medium such as classical vacuum the dispersion relation for electromagnetic waves is:

$\omega =c_{0}k$

where c₀ is the speed of light in classical vacuum. For this case, the phase and group velocities both are c₀. In so-called dispersive media the dispersion relation can be a complicated function of wavevector, and the phase and group velocities are not the same. In the general case, the phase and group velocities may have different directions.

Example: Envelope function approximation

In condensed matter physics the wavefunction for a mobile charge carrier in a crystal can be expressed as a Bloch wave:

$\psi _{n\mathbf {k} }(\mathbf {r} )=e^{i\mathbf {k} \cdot \mathbf {r} }u_{n\mathbf {k} }(\mathbf {r} ).$

where n is the index for the band (for example, conduction or valence band) r is the spatial location of the particle, and k is its wavevector. The exponential is a sinusoidally varying function corresponding to a slowly varying envelope modulating the rapidly varying part of the wavefunction u, describing the behavior of the wavefunction close to the cores of the atoms of the lattice.

In determining the behavior of the carriers using quantum mechanics, the envelope approximation usually is used in which the Schrödinger equation is simplified to refer only to the behavior of the envelope, and boundary conditions are applied to the envelope function directly, rather than to the complete wavefunction. For example, the wavefunction of a carrier trapped near an impurity is governed by an envelope function F that becomes a superposition of Bloch envelope functions:

$F(\mathbf {r} )={\frac {1}{\sqrt {V}}}\sum _{\mathbf {k} }A(\mathbf {k} )e^{i\mathbf {k\cdot r} }\ ,$

where the coefficients A(k) are found from the approximate Schrödinger equation, and V is the crystal volume.