User:John R. Brews/WP Import: Difference between revisions

From Citizendium
Jump to navigation Jump to search
imported>John R. Brews
No edit summary
imported>John R. Brews
No edit summary
Line 4: Line 4:


==BJT parameters==
==BJT parameters==
The hybrid-pi model is a linearized [[two-port network]] approximation to the transistor using the small-signal base-emitter voltage <math>v_{be}</math> and collector-emitter voltage <math>v_{ce}</math> as independent variables, and the small-signal base current <math>i_{b}</math> and collector current <math>i_{c}</math> as dependent variables. (See Jaeger and Blalock.<ref name=Jaeger1/>
The hybrid-pi model is a linearized [[two-port network]] approximation to the transistor using the small-signal base-emitter voltage <math>v_{be}</math> and collector-emitter voltage <math>v_{ce}</math> as independent variables, and the small-signal base current <math>i_{b}</math> and collector current <math>i_{c}</math> as dependent variables. (See Jaeger and Blalock.<ref name=Jaeger1/>)
[[Image:H pi model.png|frame|Figure 1: Simplified, low-frequency hybrid-pi [[BJT]] model.]]
[[Image:H pi model.png|frame|Figure 1: Simplified, low-frequency hybrid-pi [[BJT]] model.]]
A basic, low-frequency hybrid-pi model for the [[bipolar transistor]] is shown in figure 1. The various parameters are as follows.
A basic, low-frequency hybrid-pi model for the [[bipolar transistor]] is shown in figure 1. The various parameters are as follows.

Revision as of 12:43, 22 May 2011

The hybrid-pi model is a popular circuit model used for analyzing the small signal behavior of transistors. The model can be quite accurate for low-frequency circuits and can easily be adapted for higher frequency circuits with the addition of appropriate inter-electrode capacitances and other parasitic elements.

BJT parameters

The hybrid-pi model is a linearized two-port network approximation to the transistor using the small-signal base-emitter voltage Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_{be}} and collector-emitter voltage Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_{ce}} as independent variables, and the small-signal base current Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i_{b}} and collector current Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i_{c}} as dependent variables. (See Jaeger and Blalock.[1])

Figure 1: Simplified, low-frequency hybrid-pi BJT model.

A basic, low-frequency hybrid-pi model for the bipolar transistor is shown in figure 1. The various parameters are as follows.

  • Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g_m = \frac{i_{c}}{v_{be}}\Bigg |_{v_{ce}=0} = \begin{matrix}\frac {I_\mathrm{C}}{ V_\mathrm{T} }\end{matrix} } is the transconductance in siemens, evaluated in a simple model (see Jaeger and Blalock[2])
where:
  • Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_\mathrm{C} \,} is the quiescent collector current (also called the collector bias or DC collector current)
  • Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_\mathrm{T} = \begin{matrix}\frac {kT}{ q}\end{matrix}} is the thermal voltage, calculated from Boltzmann's constant, the charge on an electron, and the transistor temperature in kelvins. At 300 K (approximately room temperature) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_\mathrm{T}} is about 26 mV (Google calculator).
  • Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_{\pi} = \frac{v_{be}}{i_{b}}\Bigg |_{v_{ce}=0} = \frac{\beta_0}{g_m} = \frac{V_\mathrm{T}}{I_\mathrm{B}} \,} in ohms
where:
  • Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta_0 = \frac{I_\mathrm{C}}{I_\mathrm{B}} \,} is the current gain at low frequencies (commonly called hFE). Here Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_B} is the Q-point base current. This is a parameter specific to each transistor, and can be found on a datasheet; Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta} is a function of the choice of collector current.
  • Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_O = \frac{v_{ce}}{i_{c}}\Bigg |_{v_{be}=0} = \begin{matrix}\frac {V_A+V_{CE}}{I_C}\end{matrix} \approx \begin{matrix} \frac {V_A}{I_C}\end{matrix}} is the output resistance due to the Early effect.

Related terms

The reciprocal of the output resistance is named the output conductance

  • Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g_{ce} = \frac {1} {r_O} } .

The reciprocal of gm is called the intrinsic resistance

  • Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_{E} = \frac {1} {g_m} } .

MOSFET parameters

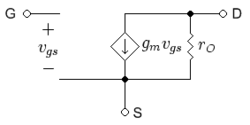
Figure 2: Simplified, low-frequency hybrid-pi MOSFET model.

A basic, low-frequency hybrid-pi model for the MOSFET is shown in figure 2. The various parameters are as follows.

  • Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g_m = \frac{i_{d}}{v_{gs}}\Bigg |_{v_{ds}=0}}

is the transconductance in siemens, evaluated in the Shichman-Hodges model in terms of the Q-point drain current Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_D} by (see Jaeger and Blalock[3]):

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ g_m = \begin{matrix}\frac {2I_\mathrm{D}}{ V_{\mathrm{GS}}-V_\mathrm{th} }\end{matrix}} ,
where:
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_\mathrm{D} } is the quiescent drain current (also called the drain bias or DC drain current)
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{th}} = threshold voltage and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{GS}} = gate-to-source voltage.

The combination:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ V_{ov}=( V_{GS}-V_{th})}

often is called the overdrive voltage.

  • Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_O = \frac{v_{ds}}{i_{d}}\Bigg |_{v_{gs}=0}} is the output resistance due to channel length modulation, calculated using the Shichman-Hodges model as
Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_O = \begin{matrix}\frac {1/\lambda+V_{DS}}{I_D}\end{matrix} \approx \begin{matrix} \frac {V_E L}{I_D}\end{matrix} } ,

using the approximation for the channel length modulation parameter λ[4]

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lambda =\begin{matrix} \frac {1}{V_E L} \end{matrix} } .

Here VE is a technology related parameter (about 4 V / μm for the 65 nm technology node[4]) and L is the length of the source-to-drain separation.

The reciprocal of the output resistance is named the drain conductance

  • Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g_{ds} = \frac {1} {r_O} } .


References and notes

  1. ↑ R.C. Jaeger and T.N. Blalock (2004). Microelectronic Circuit Design, Second Edition. New York: McGraw-Hill, Section 13.5, esp. Eqs. 13.19. ISBN 0-07-232099-0. 
  2. ↑ R.C. Jaeger and T.N. Blalock. Eq. 5.45 pp. 242 and Eq. 13.25 p. 682. ISBN 0-07-232099-0. 
  3. ↑ R.C. Jaeger and T.N. Blalock. Eq. 4.20 pp. 155 and Eq. 13.74 p. 702. ISBN 0-07-232099-0. 
  4. ↑ 4.0 4.1 W. M. C. Sansen (2006). Analog Design Essentials. Dordrechtμ: Springer. ISBN 0-387-25746-2. 
Retrieved from "https://citizendium.org/wiki/index.php?title=User:John_R._Brews/WP_Import&oldid=816849"