Liénard–Wiechert potentials
The Liénard–Wiechert potentials are scalar and vector potentials that allow determination of exact solutions of the Maxwell equations for the electric field and magnetic flux density generated at an arbitrary location by an ideal point charge moving in a trajectory prescribed in advance (not calculated from any dynamical model). Because the trajectory is prescribed, the charge is forced to follow its trajectory unaffected by its radiation of energy and momentum.
Point charges are an idealization, of course. Calculation of fields produced by charged bodies of non-zero extent, such as electrons, is more complicated. Among other matters, the dimensions of the moving charge are affected by its motion and potentially by its interaction with the fields it generates. Thus, dynamics intrudes once non-zero dimensions are introduced. For some specialized problems, quantum electrodynamics provides answers, but for a broader range of practical problems, non-relativistic electrodynamics is used.[1]
Mathematical results
In the following discussion, SI units are used.
Define β in terms of the velocity v of a point charge at time t as:
and unit vector û as
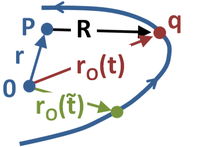
Here R is the vector joining the observation point P to the moving charge q at the time t. Also, c0 is the defined value for the speed of light in classical vacuum. Referring to the figure, the Liénard–Wiechert potentials consist of a scalar potential Φ and a vector potential A. The scalar potential is:[2]
where the tilde ‘ ~ ’ denotes evaluation at the retarded time, defined implicitly as:
r the location of the observation point, and rO being the location of the particle on its trajectory. The symbol ε0 is the electric constant of the SI units. Notice that at time , unit vector û() points at the retarded position of the charge.
The vector potential is:
The symbol μ0 is the magnetic constant of the SI units.With these potentials the electric field and the magnetic flux density are found to be (dots over symbols are time derivatives):[2][3][4]
If the particle does not accelerate, the first term alone survives and for velocities much less than the speed of light the result is the Biot-Savart law. If the particle accelerates, the last term is called the radiation field, and is associated with the emission of energy and momentum by the moving charge. The Biot-Savart term drops off more quickly with distance, and is called the near field term. The radiation field drops off more slowly with distance, so it dominates the result at large distances and is called the far field term.
Notes
- ↑ Herbert Spohn (2004). Dynamics of charged particles and their radiation field. Cambridge University Press. ISBN 0521836972.
- ↑ 2.0 2.1 Fulvio Melia (2001). “§4.6.1 Point currents and Liénard-Wiechert potentials”, Electrodynamics. University of Chicago Press, pp. 101. ISBN 0226519570.
- ↑ Harald J. W. Müller-Kirsten (2004). Electrodynamics: an introduction including quantum effects. World Scientific, p. 223. ISBN 9812388087.
- ↑ Kurt Edmund Oughstun (2006). “§3.3.2: The field produced by a moving charged particle”, Electromagnetic and optical pulse propagation. Springer, p. 134. ISBN 038734599X.






![{\displaystyle {\boldsymbol {E}}({\boldsymbol {r}},\ t)=-{\boldsymbol {\nabla }}\Phi -{\frac {\partial }{\partial t}}{\boldsymbol {A}}={\frac {q}{4\pi \varepsilon _{0}}}\left[{\frac {(\mathbf {\hat {u}} -{\boldsymbol {\beta }})(1-\beta ^{2})}{(1-\mathbf {\hat {u}} \mathbf {\cdot } {\boldsymbol {\beta }})^{3}R^{2}}}+{\frac {\mathbf {{\hat {u}}\ \mathbf {\times } \ } [({\hat {\mathbf {u} }}-{\boldsymbol {\beta }})\ \mathbf {\times } \ {\boldsymbol {\dot {\beta }}}]}{c_{0}(1-\mathbf {{\hat {u}}\cdot } {\boldsymbol {\beta }})^{3}R}}\right]_{\tilde {t}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e1de9f1eeac689c0c595b8fda6acc73c626ccf5)
