Green's function: Difference between revisions
imported>Paul Wormer (→Proof) |
imported>Paul Wormer |
||
| Line 58: | Line 58: | ||
:<math> | :<math> | ||
\Phi(\mathbf{x}) = \frac{1}{4\pi \epsilon_0} \iiint\; \frac{\rho(\mathbf{y})}{|\mathbf{x}-\mathbf{y}|} | \Phi(\mathbf{x}) = \frac{1}{4\pi \epsilon_0} \iiint\; \frac{\rho(\mathbf{y})}{|\mathbf{x}-\mathbf{y}|} | ||
\;\mathrm{d}\mathbf{y} | \;\mathrm{d}\mathbf{y}. | ||
</math> | </math> | ||
===Proof=== | Indeed, | ||
:<math> | |||
\nabla^2 \Phi(\mathbf{x}) = \frac{1}{4\pi \epsilon_0} \iiint\; \rho(\mathbf{y}) \nabla^2\frac{1}{|\mathbf{x}-\mathbf{y}|} \;\mathrm{d}\mathbf{y} = -\frac{4\pi}{4\pi\epsilon_0} | |||
\iiint\; \rho(\mathbf{y}) \delta(\mathbf{x}-\mathbf{y}) \;\mathrm{d}\mathbf{y} = -\frac{\rho(\mathbf{x})}{\epsilon_0}. | |||
</math> | |||
The integral form of the electrostatic field may be seen as a consequence of [[Coulomb's law]]. The field at the point '''''x''''' due to the charge d''Q'' = ρ('''''y''''')d'''''y''''' is equal to | |||
:<math> | |||
d\Phi(\mathbf{x}) = \frac{dQ}{4\pi\epsilon_0 |\mathbf{x}-\mathbf{y}|}. | |||
</math> | |||
The field is additive in the charges, so integration gives the total field at '''''x'''''. | |||
===Proof of Green function of ∇<sup>2</sup>=== | |||
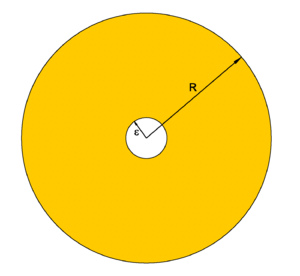
[[Image:Green delta.png|right|300px|thumb|Integration regions: yellow domain is ''U''<sub>ε</sub>, large sphere is ''V''<sub>''R''</sub>, small sphere is ''V''<sub>ε</sub>]] | [[Image:Green delta.png|right|300px|thumb|Integration regions: yellow domain is ''U''<sub>ε</sub>, large sphere is ''V''<sub>''R''</sub>, small sphere is ''V''<sub>ε</sub>]] | ||
Without loss of generality we take '''''x''''' as the origin (0, 0, 0) and replace '''''y''''' by '''''r''''' = (''x'', ''y'', ''z'') in the above formulation. The length of '''''r''''' is indicated by ''r''. | Without loss of generality we take '''''x''''' as the origin (0, 0, 0) and replace '''''y''''' by '''''r''''' = (''x'', ''y'', ''z'') in the above formulation. The length of '''''r''''' is indicated by ''r''. | ||
| Line 92: | Line 104: | ||
because by assumption φ and its gradient vanish on ''S''<sub>''R''</sub>. | because by assumption φ and its gradient vanish on ''S''<sub>''R''</sub>. | ||
We consider the integral on the right hand side and we will | We consider the integral on the right hand side and we will show that | ||
:<math> | :<math> | ||
\iiint\limits_{V_R} \frac{1}{r} \nabla^2\phi\, d V = -4\pi \phi(\mathbf{0}), | \iiint\limits_{V_R} \frac{1}{r} \nabla^2\phi\, d V = -4\pi \phi(\mathbf{0}), | ||
</math> | </math> | ||
from which the result to be proved | from which the result to be proved directly. The main trick is to write | ||
:<math> | :<math> | ||
\iiint\limits_{V_R} \frac{1}{r} \nabla^2\phi\, d V = \lim_{\epsilon \rightarrow 0} \iiint\limits_{U_\epsilon} \frac{1}{r} \nabla^2\phi\, d V | \iiint\limits_{V_R} \frac{1}{r} \nabla^2\phi\, d V = \lim_{\epsilon \rightarrow 0} \iiint\limits_{U_\epsilon} \frac{1}{r} \nabla^2\phi\, d V | ||
| Line 126: | Line 138: | ||
and that the value of the gradient averaged over the surface may be taken out of the integral. The remaining surface integral is equal to 4πε<sup>2</sup>. | and that the value of the gradient averaged over the surface may be taken out of the integral. The remaining surface integral is equal to 4πε<sup>2</sup>. | ||
In order to evaluate the final integral we use | |||
:<math> | |||
\boldsymbol{\nabla} \frac{1}{r} = - \frac{\mathbf{r}}{r^3} \equiv -\frac{\mathbf{e}_r}{r^2} \qquad | |||
\hbox{and}\qquad d\mathbf{S} = \mathbf{e}_r \;r^2\sin\theta\,d\phi d\theta | |||
</math> | |||
so that | |||
:<math> | |||
\iint\limits_{S_\epsilon} \big(\phi \boldsymbol{\nabla}\frac{1}{r}\big) \cdot d\mathbf{S} | |||
= | |||
-\iint\limits_{S_\epsilon} \phi(\mathbf{r}) \sin\theta\,d\phi d\theta = -\phi(\epsilon) \; 4\pi. | |||
</math> | |||
The limit ε → 0 gives the desired result. | |||
==References== | ==References== | ||
* P. Roman, ''Advanced Quantum Theory'', Addison-Wesley, Reading, Mass. (1965) Appendix 4. | * P. Roman, ''Advanced Quantum Theory'', Addison-Wesley, Reading, Mass. (1965) Appendix 4. | ||
* I. M. Gel'fand and G. E. Shilov, ''Generalized Functions'', Vol. 1, Academic Press, New York (1964) | * I. M. Gel'fand and G. E. Shilov, ''Generalized Functions'', Vol. 1, Academic Press, New York (1964) | ||
Revision as of 08:58, 9 January 2009
In physics and mathematics, Green's functions are auxiliary functions in the solution of linear partial differential equations. Green's function is named for the British mathematician George Green (1793 – 1841).
Definition
Let Lx be a given linear differential operator in n variables x = (x1, x2, ..., xn), then the Green function of Lx is the function G(x,y) defined by
where δ(x-y) is the Dirac delta function. Once G(x,y) is known, any differential equation involving Lx is formally solved. Suppose we want to solve,
for a known right hand side ρ(x). The formal solution is
The proof is by verification,
where in the last step the defining property of the Dirac delta function is used.
The integral operator that has the Green function as kernel may be seen as the inverse of a linear operator,
It is illuminating to make the analogy with matrix equations. Let and be n×n matrices connected by
then the solution of a matrix-vector equation is
Make the correspondence i ↔ x, j ↔ y, and compare the sum over j with the integral over y, and the correspondence is evident.
Example
We consider a case of three variables, n = 3 with x = (x, y, z).
The Green function of
is
As an important example of this Green function we mention that the formal solution of the Poisson equation of electrostatics, reading
where ε0 is the electric constant and ρ is a charge distribution, is given by
Indeed,
The integral form of the electrostatic field may be seen as a consequence of Coulomb's law. The field at the point x due to the charge dQ = ρ(y)dy is equal to
The field is additive in the charges, so integration gives the total field at x.
Proof of Green function of ∇2
Without loss of generality we take x as the origin (0, 0, 0) and replace y by r = (x, y, z) in the above formulation. The length of r is indicated by r.
The proof uses Green's theorem:
where Va is a sphere with radius a and Sa is the surface of this sphere. The smooth test function φ and its gradient vanish for large r,
Further we notice that
because r ≠ 0 in that region (see the figure, where the region is indicated in yellow). This result is most easily proved if we recall that in spherical polar coordinates
First apply Green's theorem to the large sphere of radius R
because by assumption φ and its gradient vanish on SR.
We consider the integral on the right hand side and we will show that
from which the result to be proved directly. The main trick is to write
and to consider first the integral over Uε (the yellow domain in the figure) for non-zero ε. After the integral has been evaluated, the limit for zero ε is taken.
Since Uε has two surfaces, Green's theorem cannot be applied directly, and therefore we write (see the figure),
and apply Green's theorem to the two terms. Recalling that we saw already the first term, we get
The integral between square brackets is zero because ∇2(1/r) is zero on Uε. The last integral can be shown to vanish for small ε. Because φ and its gradient are smooth and finite, and r is constant (equal to ε) on the surface, we may write for small ε
where we assumed that
and that the value of the gradient averaged over the surface may be taken out of the integral. The remaining surface integral is equal to 4πε2.
In order to evaluate the final integral we use
so that
The limit ε → 0 gives the desired result.
References
- P. Roman, Advanced Quantum Theory, Addison-Wesley, Reading, Mass. (1965) Appendix 4.
- I. M. Gel'fand and G. E. Shilov, Generalized Functions, Vol. 1, Academic Press, New York (1964)























![{\displaystyle {\begin{aligned}\iiint \limits _{U_{\epsilon }}{\frac {1}{r}}\nabla ^{2}\phi \,dV&=\left[\iiint \limits _{V_{R}}\phi \nabla ^{2}{\frac {1}{r}}\,dV-\iiint \limits _{V_{\epsilon }}\phi \nabla ^{2}{\frac {1}{r}}\,dV\right]+\iint \limits _{S_{\epsilon }}{\big (}\phi {\boldsymbol {\nabla }}{\frac {1}{r}}{\big )}\cdot d\mathbf {S} -\iint \limits _{S_{\epsilon }}{\big (}{\frac {1}{r}}{\boldsymbol {\nabla }}\phi {\big )}\cdot d\mathbf {S} \\&=\left[\iiint \limits _{U_{\epsilon }}\phi \nabla ^{2}{\frac {1}{r}}\,dV\right]+\iint \limits _{S_{\epsilon }}{\big (}\phi {\boldsymbol {\nabla }}{\frac {1}{r}}{\big )}\cdot d\mathbf {S} -\iint \limits _{S_{\epsilon }}{\big (}{\frac {1}{r}}{\boldsymbol {\nabla }}\phi {\big )}\cdot d\mathbf {S} \\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe23b682772a037b0453c03e020506a09bf82273)



