Gravitational lens: Difference between revisions
imported>Jori Liesenborgs |
imported>Jori Liesenborgs (→Lens equation: thin lens approximation and generalized deflection angle) |
||
| Line 90: | Line 90: | ||
=== Lens equation === | === Lens equation === | ||
Since the distances involved in gravitational lensing are enormous compared to the distance scale at which the deflection takes place, | |||
the mass distribution of the gravitational lens is approximated as a two-dimensional one, located in the so-called ''lens plane''. | |||
If the ''z''-axis lies along the source-lens direction, this two-dimensional mass distribution <math>\Sigma</math> can be obtained | |||
from the three-dimensional distribution <math>\rho</math> as follows: | |||
<math>\Sigma(\vec{\xi}) = \int\rho(\xi_1,\xi_2,z)\mathrm{d}z</math>, | |||
where <math>\vec{\xi}</math> is a vector in the lens plane. | |||
Light rays are then assumed to travel in a straight line from the source to the lens plane. At this point, they are deflected and | |||
continue along a straight path towards the observer. The situation is illustrated in the figure below. Projecting the path of a | |||
light ray (thick black line) onto the ''xz'' and ''yz'' planes shows the two angles <math>\hat{\alpha}_x</math> and <math>\hat{\alpha}_y</math> | |||
needed to describe the gravitational deflection. These are the components of a vector-based bending angle <math>\vec{\hat{\alpha}}</math>. | |||
Based on Einstein's expression for the bending angle due to a point mass, the gravitational deflection of an arbitrary two-dimensional | |||
mass distribution <math>\Sigma</math> can easily be seen to be: | |||
<math>\vec{\hat{\alpha}}(\vec{\xi}) = \frac{4 G}{c^2}\int \frac{\Sigma(\vec{\xi}')(\vec{\xi}-\vec{\xi}')}{|\vec{\xi}-\vec{\xi}'|^2} \mathrm{d}^2 \xi'</math>. | |||
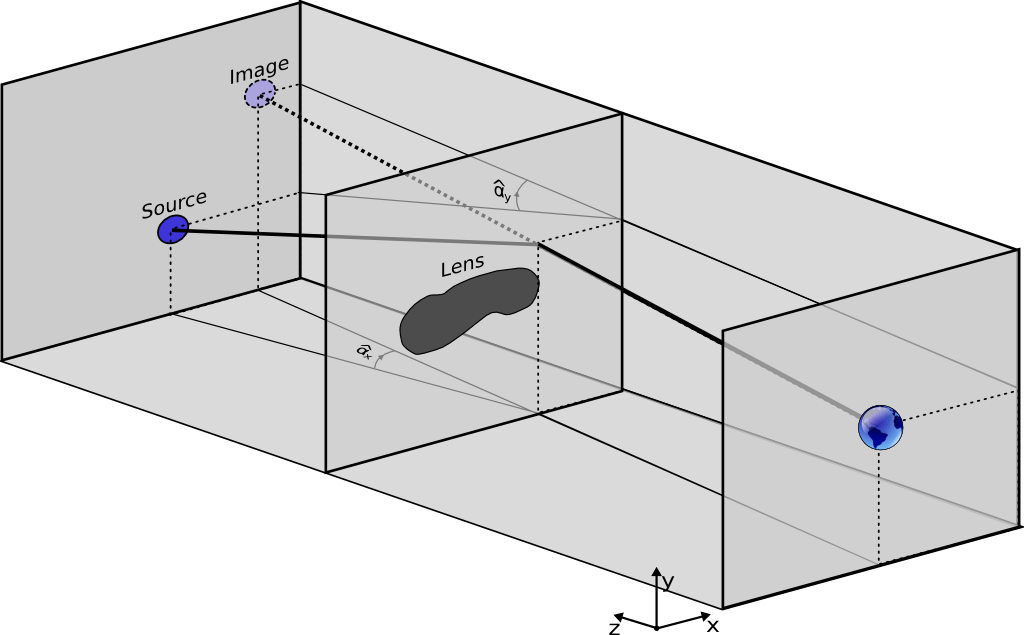
[[Image:ThinLensApproximation3D.png|left|frame|In the thin lens approximation, a light ray (thick black line) goes in a straight line from the source to the lens plane, in which a two-dimensional mass distribution is located. The light ray is deflected instantaneously and continues again along a straight line to the observer. Projections on the ''xz'' and ''yz'' planes identify the two components of a vector-based bending angle <math>\vec{\hat{\alpha}}</math>.]] | [[Image:ThinLensApproximation3D.png|left|frame|In the thin lens approximation, a light ray (thick black line) goes in a straight line from the source to the lens plane, in which a two-dimensional mass distribution is located. The light ray is deflected instantaneously and continues again along a straight line to the observer. Projections on the ''xz'' and ''yz'' planes identify the two components of a vector-based bending angle <math>\vec{\hat{\alpha}}</math>.]] | ||
Revision as of 17:55, 10 March 2007
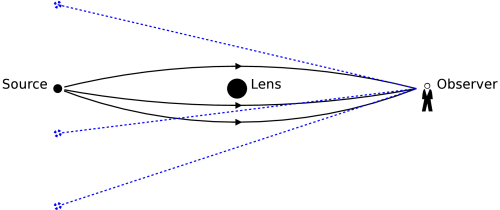
In a gravitational lensing scenario, light traveling from a distant astronomical source (e.g. a galaxy) to an observer is deflected by the gravitational field of an intermediate object: the gravitational lens (e.g. a cluster of galaxies). Because of this, the observer will see the source in a slightly different direction. Furthermore, it is possible for light rays to reach the observer by multiple paths, causing multiple images of the same source to appear.
History
In Newtonian mechanics, the path of a test particle in a gravitational field does not depend on the mass of the particle. For this reason, one can argue that even in the absolute space and time of Newton, light does not always go in a straight line, but can be deflected noticeably by objects with a sufficiently strong gravitational field. In 1804, J. von Soldner was the first one to publish the Newtonian value of the deflection angle (as illustrated in the figure on the right):
In this equation, G is the gravitational constant, M the mass of the object deflecting the light, c is the speed of light and d is the distance of closest approach.
More than a century later, after having completed his general theory of relativity, Albert Einstein published a new expression, differing by a factor of two from the Newtonian result:
For a light ray passing close to the Sun, the value of this angle is 1.74 seconds of arc. During a solar eclipse, the bending angle can be calculated by comparing the positions of stars close to the sun to the positions where one would expect these stars to be seen if their light rays were not deflected by the sun. In 1919, a team of astronomers led by Eddington set out to measure the deflection angle during a total eclipse and reported an agreement with Einstein's predicted value with an uncertainty measure of 20%. Later measurements drastically reduced this amount of uncertainty to a value of 0.02%.
After this, gravitational deflection of light received only little attention for a very long time. Around 1964 Liebes and especially Refsdal revived the gravitational lens effect briefly, but it wasn't until the first actual gravitationally lensed quasar QSO 0957+561 was observed in 1979 that the subject gained much interest. Since then, a huge amount of articles about gravitational lensing have been published.
Regimes
Gravitational lens phenomena are usually subdivided into three categories: strong lensing, weak lensing and microlensing. In the strong lensing regime, the gravitational lens effect causes multiple images of the same source to be observed. Often, there are severely distorted images such as giant arcs. For strong lensing to occur, the source, the gravitational lens and the observer have to be sufficiently well aligned and the bending angle has to be large enough to allow the different images to be resolved. Some strong lensing examples include:
- SDSS J1004+4112: here, a cluster of galaxies acts as a gravitational lens, producing five images of a distant quasar and three of a distant galaxy.
- G2237+0305: a galaxy causes four images of a distant quasar to appear. This gravitational lens is often referred to as the Einstein Cross.
- CL 0024+1654: a cluster of galaxies (yellow) creates several images of a distant galaxy (blue).
In some cases the alignment is not well enough to produce multiple images, but the effect of the gravitational lens can still be seen through the presence of a multitude of slightly distorted images. This is normally referred to as weak lensing. Since it is impossible to know the exact shape of a source a priori, a statistical analysis of a large number of images is necessary to acquire information about the distortions caused by the gravitational lens.
Finally, it is possible that the gravitational lens does cause multiple images, but that these simply cannot be resolved by our telescopes. However, since a gravitational lens can cause images to become brighter, the presence of a gravitational lens can be detected when source and lens move with respect to each other. In this case, the gravitational lens effect is referred to as microlensing.
Lensing formalism
To describe the gravitational lens effect, usually the lensing formalism described below is employed. This framework is only valid if the angles involved are small and if the gravitational field is not too strong. It can be applied to lensing by stars, galaxies and clusters of galaxies, but not to strong deflection by a black hole for example.
Deflection angle
To derive the deflection angle predicted by general relativity, one usually starts from a space-time continuum described by the static weak-field metric, which has the following line element:
.
Here, is the Newtonian gravitational potential of the lensing mass. It can be shown that the path of a light ray in this metric is mathematically equivalent to the path of a light ray in Newton's absolute space and time if there's a location-dependent refractive index
.
Fermat's theorem from geometric optics says that light goes from source to destination using paths for which the corresponding time delay is extremal. Applying this principle to calculate the deflection angle for a point mass leads to Einstein's expression:
.
Lens equation
Since the distances involved in gravitational lensing are enormous compared to the distance scale at which the deflection takes place, the mass distribution of the gravitational lens is approximated as a two-dimensional one, located in the so-called lens plane. If the z-axis lies along the source-lens direction, this two-dimensional mass distribution can be obtained from the three-dimensional distribution as follows:
,
where is a vector in the lens plane.
Light rays are then assumed to travel in a straight line from the source to the lens plane. At this point, they are deflected and continue along a straight path towards the observer. The situation is illustrated in the figure below. Projecting the path of a light ray (thick black line) onto the xz and yz planes shows the two angles and needed to describe the gravitational deflection. These are the components of a vector-based bending angle . Based on Einstein's expression for the bending angle due to a point mass, the gravitational deflection of an arbitrary two-dimensional mass distribution can easily be seen to be:
.
Brightness of the images
Time delay
Applications
Cosmic telescope
As is mentioned above, a gravitational lens can have a serious effect on how the observer perceives an astronomical object. It is possible that one of the images (or several images) are stretched severely, and precisely these images will also become brighter. Because of this, a gravitational lens can make very distant objects visible, which would otherwise be far to dim to observe. For this reason, gravitational lenses are sometimes referred to as cosmic telescopes.
Abell 2218 is a cluster of galaxies acting as a gravitational lens for several background objects. Thanks to its magnifying effect, an extremely distant galaxy has been observed.[1]
Detection of planets
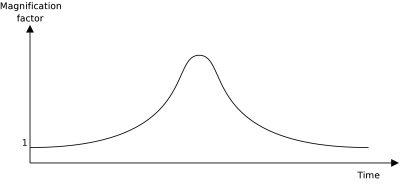
When an object moves with respect to another star acting as a gravitational lens, this will produce a typical brightness curve such as the one on the right. If a planet orbits the star acting as a gravitational lens, it is possible that the measured brightness curve reveals the presence of this planet by introducing an additional small bump for example. The advantage of this planet detection method is that it permits the discovery of planets having masses of only a small fraction of the star's mass. A handful of planets has already been detected this way.[2] [3]
Lens inversion
When you know where the source would be in absence of a gravitational lens and the mass distribution of the lens is known as well, it is relatively easy to calculate the images caused by the gravitational lens effect. Of course, in practice you neither know the position of the source nor the exact mass distribution of the lens. Instead we face the inverse problem: if we know the images caused by the gravitational lens effect, what is the mass distribution which makes them appear.
Lens-inversion techniques are usually subdivided into two classes. Parametric methods use a specific model for the mass distribution, for example an elliptical one. Using the images of one or more sources as input, the inversion routine then tries to find the parameters of the lens (position, ellipticity, rotation) which fit these images best. Non-parametric methods do not assume a particular shape of the mass distribution. One way to do this is to assume a mass distribution to be the sum of a large number of basis functions, the weights of which are determined by an inversion routine.
All matter present in the gravitational lens contributes to the gravitational bending of light rays. Because of this, gravitational lens inversion provides an independent probe of the mass of a galaxy or a cluster of galaxies. If the mass density retrieved in this way is compared to the visible amount of matter, this provides a great deal of information about the presence of dark matter.[4]
Cosmological parameters
Because of the deflection of light by a gravitational lens, light rays from a source can reach an observer using multiple paths. The time it takes light to travel from source to observer is in general different for each path. If the source is one of varying brightness, measuring the brightness curves for each image for a while can reveal information about the relative time delays. It is easy to see that the expansion of the universe influences the time it takes light to go from source to observer. The Hubble constant describes this rate of expansion and for this reason, the relative time delays between the images of a source can provide constraints on the value of the Hubble constant.
The gravitational lens effect can also supply information about other cosmological parameters. For example, statistical information about the occurence of gravitationally lensed object can provide insight into the values of the matter density and the cosmological constant.