Electromagnetic wave

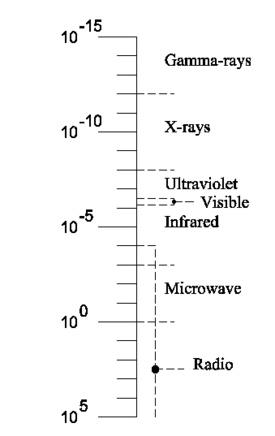
In physics, an electromagnetic wave is a change, periodic in space and time, of an electric field E(r,t) and a magnetic field B(r,t). A stream of electromagnetic waves is referred to as electromagnetic radiation. Because an electric as well as a magnetic field is involved, the term electromagnetic is used, a contamination of electric and magnetic. Examples of electromagnetic waves, in increasing wavelength, are: gamma rays, X-rays, ultraviolet light, visible light, infrared, microwaves, and radio waves. All these waves propagate in vacuum with the same speed c, the speed of light. With regard to propagation of electromagnetic waves, air at standard temperature and pressure is very close to vacuum (its refractive index 1.0002926 is very close to the exact vacuum value 1).

Electromagnetic waves were predicted on theoretical grounds by James Clerk Maxwell in 1861 and first emitted and received in the laboratory by Heinrich Hertz a quarter century later. The first to see the applicability for communication purposes was the inventor of radiotelegraphy Guglielmo Marconi (around 1900). Later applications are radio, television, radar, cellular phones, gps, and all kinds of wireless applications, from remote control of televison sets to internet access in public places.

Fig. 1. Electromagnetic wave. Electric component (red) in plane of drawing; magnetic component (blue) in orthogonal plane. Wave propagates to the right. The wavelength is λ.

Properties

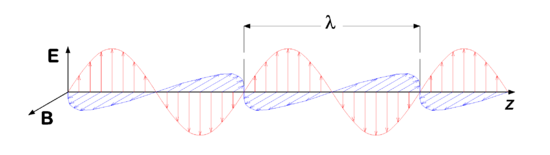
In figure 1 we see a snapshot (i.e., a picture at a certain point in time) of the magnetic and electric fields in adjacent points of space. In each point, the vector E is perpendicular to the vector B. The wave propagates to the right, along an axis which we conveniently refer to as y-axis. Both E and B are perpendicular to the propagation direction, which is expressed by stating that an electromagnetic wave is a transverse wave, in contrast to sound waves, which are longitudinal waves (i.e., air molecules vibrate parallel to the propagation direction of the sound).

Assume that the snapshot in figure 1 is taken at time t, then at a certain point y we see an arrow of certain length representing E(y,t) and also a vector B(y,t). At a point in time Δt later, the same values of E and B (same arrows) are seen at y + c Δt. The arrows seem to have propagated to the right with a speed c.

Fig. 2. Schematic overview of electromagnetic spectrum. Vertical axis: wavelengths in meter. Examples: infrared extends from 8 ·10⁻⁷ to 10⁻³ m; radio from 10⁻⁴ to about 10⁴ m.

In figure 1, the time t is fixed and the position y varies. Conversely, we can keep the position fixed and imagine what happens if time changes. Focus on a fixed point y, then in progressing time the two vectors E(y,t) and B(y,t) in the point y, grow to a maximum value, then shrink to zero, become negative, go to a minimum value, and grow again, passing through zero, they grow to the same maximum value again. This cycle is repeated indefinitely. When we now plot E and B in the fixed point y as a function of time t, we see the same type (sine-type) function as in figure 1. The number of times per second that the vectors go through a full cycle is the frequency of the electromagnetic wave.

Periodicity in space means that the electromagnetic (EM) wave is repeated after a certain distance. This distance, the wavelength is traditionally designated by λ, see figure 1. If we go at a fixed time a distance λ to the right or to the left we encounter the very same fields E and B.

Basically, the only property distinguishing different kinds of EM waves, is their wavelength, see figure 2. Note the enormous span in wavelengths, from one trillionth of a millimeter for gamma-rays (radioactive rays) up to the VLF (very low frequency) radiowaves of about 100 kilometer.

Frequency of electromagnetic waves

Often EM waves are characterized by their frequency (the number of cycles per unit time), instead of by their wavelength. If the EM field goes through ν full cycles in a second, where ν is a positive integral number, we say that the field has a frequency of ν Hz (hertz). In 1/ν second the wave propagates a distance c/ν meter, which is the wavelength λ:

$\lambda ={\frac {c}{\nu }}\quad \Longrightarrow \quad \nu ={\frac {c}{\lambda }}$

If we express c in m/s then λ is obtained in m. To convert quickly from wavelength to frequency we can approximate c by 3·10⁸ m/s. Thus, for instance,

λ = 3·10⁻¹⁰ m → ν = 10¹⁸ Hz (X-ray)

λ = 6·10⁻⁷ m → ν = 5·10¹⁴ Hz (Visible, orange)

λ = 3·10⁻² m  → ν = 10¹⁰ Hz = 10GHz (Microwave)

λ = 3·10² m   → ν = 10⁶ Hz = 1 MHz (Radiowave)

Monochromatic linearly polarized waves

It is known that EM waves can be linearly superimposed, which is due to the fact that they are solutions of a linear partial differential equation, the wave equation (see next section). A linear superposition of waves is a solution of the same wave equation as the waves themselves. Such a superposition is also an electromagnetic wave (a propagating periodic disturbance of the EM field). If waves of different wavelengths are superimposed, then a non-monochromatic wave is obtained (the term multi-chromatic wave would be apt, but is hardly ever used). By means of Fourier analysis a non-monochromatic wave can be decomposed into monochromatic components. The wave in figure 1 has one wavelength, it is a monochromatic wave.

The electric field vectors in figure 1 are all in one plane, this is the plane of polarization, and a wave with one fixed polarization plane, is called linearly polarized.

The radiation of many lasers is monochromatic and linearly polarized (at least to a very good approximation).

Relation to Maxwell's equations

In this section it will be shown that the electromagnetic wave depicted in figure 1 is a solution of the Maxwell equations in the vacuum.

We assume that at some distance away from the source of EM waves (a radio transmitter, a laser, gamma radiating nuclei, etc.), there is no charge density ρ and no current density J. For that region of space, the microscopic (vacuum) Maxwell equations become (in SI units):

${\boldsymbol {\nabla }}\cdot \mathbf {B} =0,\qquad {\boldsymbol {\nabla }}\cdot \mathbf {E} =0,$

and

${\boldsymbol {\nabla }}\times \mathbf {B} ={\frac {1}{c^{2}}}{\frac {\partial \mathbf {E} }{\partial t}},\qquad {\boldsymbol {\nabla }}\times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}.$

Apply to the last Maxwell equation the following relation, known from vector analysis and valid for any (differentiable) vector field,

${\boldsymbol {\nabla }}\times ({\boldsymbol {\nabla }}\times \mathbf {E} )={\boldsymbol {\nabla }}({\boldsymbol {\nabla }}\cdot \mathbf {E} )-{\boldsymbol {\nabla }}^{2}\mathbf {E}$

and use that ∇ · E = 0, then E satisfies the wave equation,

${\boldsymbol {\nabla }}^{2}\mathbf {E} ={\frac {\partial ({\boldsymbol {\nabla }}\times \mathbf {B} )}{\partial t}}={\frac {1}{c^{2}}}{\frac {\partial ^{2}\mathbf {E} }{\partial t^{2}}}.$

Note that the displacement current (time derivative of E) is essential in this equation, if it were absent (zero), the field E would be a static, time-independent, electric field, and there would be no waves.

In the very same way we derive a wave equation for B,

${\boldsymbol {\nabla }}^{2}\mathbf {B} ={\frac {1}{c^{2}}}{\frac {\partial ^{2}\mathbf {B} }{\partial t^{2}}}.$

Observe that E and B are related by the third and fourth Maxwell equation, which express the fact that a displacement current causes a magnetic field, and a changing magnetic field causes an electric field (Faraday's law of induction), respectively. So a time-dependent electric field that is not associated with a time-dependent magnetic field cannot exist, and conversely. Indeed, in special relativity E and c B can be transformed into one another by a Lorentz transformation of the electromagnetic field tensor, which shows their close relationship.

The wave equation is without doubt the most widely studied differential equation in mathematical physics. In figure 1 the electric field depicts a particular solution, with special initial and boundary conditions. The snapshot that is depicted has the analytic form

$\mathbf {E} (\mathbf {r} ,t)=\mathbf {e} _{z}E_{0}\sin {\big [}k(y-ct){\big ]}\quad {\hbox{with}}\quad k\equiv {\frac {2\pi }{\lambda }}.$

The snapshot is taken at $\scriptstyle t=2\pi n/(ck)$ for some arbitrary integer n. We assumed here that the direction of E defines the direction of the z-axis with unit vector e_z along this axis. The quantity E₀ is the amplitude of the wave. Insertion of this expression in in the left hand side of the wave equation for E gives

${\boldsymbol {\nabla }}^{2}\mathbf {E} =\mathbf {e} _{z}E_{0}{\frac {\partial ^{2}\sin {\big [}k(y-ct){\big ]}}{\partial y^{2}}}=-k^{2}\mathbf {e} _{z}E_{0}\sin {\big [}k(y-ct){\big ]}.$

Insertion of this expression in in the right hand side of the wave equation for E gives

${\frac {\mathbf {e} _{z}E_{0}}{c^{2}}}{\frac {\partial ^{2}\sin {\big [}k(y-ct){\big ]}}{\partial t^{2}}}=-{\frac {c^{2}\,k^{2}}{c^{2}}}\mathbf {e} _{z}E_{0}\sin {\big [}k(y-ct){\big ]}=-k^{2}\mathbf {e} _{z}E_{0}\sin {\big [}k(y-ct){\big ]},$

so that it follows that the special solution, depicted in figure 1, is indeed a solution of the wave equation for E.

We could now proceed in the very same way and solve the wave equation for B, but then we could easily overlook the relation between the two fields. So we rather substitute the solution for E into the fourth Maxwell equation and use the definition of curl as a determinant,

${\begin{vmatrix}\mathbf {e} _{x}&\quad \mathbf {e} _{y}&\mathbf {e} _{z}\\{\frac {\partial }{\partial x}}&\quad {\frac {\partial }{\partial y}}&{\frac {\partial }{\partial z}}\\0&\quad 0&E_{0}\sin {\big [}k(y-ct){\big ]}\\\end{vmatrix}}=k\mathbf {e} _{x}E_{0}\cos {\big [}k(y-ct){\big ]}=-{\frac {\partial \mathbf {B} }{\partial t}}.$

It is easy to see that

$\mathbf {B} (\mathbf {r} ,t)=\mathbf {e} _{x}B_{0}\sin {\big [}k(y-ct){\big ]}\quad {\hbox{with}}\quad B_{0}\equiv {\frac {E_{0}}{c}}$

is a solution of this equation. It follows that E and B are perpendicular (along the z-axis and x-axis, respectively) and are in phase. That is, E and B are simultaneously zero and attain simultaneously their maximum and minimum. The fact that (in vacuum) the amplitude of B is a factor c smaller than of E is due to the use of SI units, in which the amplitudes have different dimensions. In Gaussian units this is not the case and E₀ = B₀.

Energy

Recall from elementary electricity theory the laws of Joule and Ohm . They state that the amount of energy W per unit time, given off by a conduction current I to its environment, is equal to

$W=I^{2}\,R=I\,V,\quad {\hbox{with}}\quad R,\,W>0,$

where R is the resistance and V a voltage difference. Joule's law implies a change in energy of −W per unit time of the system containing the current.

Assuming that the current flows along z, we introduce the current density J_z, and using

$V=-E_{z}\Delta z,\quad I=J_{z}\Delta x\Delta y$

we obtain

$W=-E_{z}J_{z}\,\Delta x\Delta y\Delta z.$

We could continue discussing the system of volume $\Delta x\Delta y\Delta z$. However, because all equations would contain the same volume, it is more convenient to consider densities and to divide out the volume. Nevertheless we still refer to the system. Thus, we define

${\mathcal {E}}_{\textrm {Joule}}\equiv -{\frac {W}{\Delta x\Delta y\Delta z}}=\mathbf {E} \cdot \mathbf {J} <0.$

The negative quantity $\scriptstyle {\mathcal {E}}_{\textrm {Joule}}$ is the change of energy of the system per unit time and per unit volume, due to the donation of energy by the system to the environment (according to Joule's law).

Apply Maxwell's equations:

$\mathbf {E} \cdot \mathbf {J} =\mathbf {E} \cdot \left(-\epsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}+{\frac {1}{\mu _{0}}}{\boldsymbol {\nabla }}\times \mathbf {B} \right)$

Use

$\mathbf {E} \cdot ({\boldsymbol {\nabla }}\times \mathbf {B} )=\mathbf {B} \cdot ({\boldsymbol {\nabla }}\times \mathbf {E} )-{\boldsymbol {\nabla }}\cdot (\mathbf {E} \times \mathbf {B} )=-\mathbf {B} \cdot \left({\frac {\partial \mathbf {B} }{\partial t}}\right)-{\boldsymbol {\nabla }}\cdot (\mathbf {E} \times \mathbf {B} )$

Define

${\mathcal {E}}_{\textrm {Field}}\equiv {\frac {1}{2}}\left(\epsilon _{0}E^{2}+{\frac {1}{\mu _{0}}}B^{2}\right)={\frac {1}{2}}\left(\mathbf {E} \cdot \mathbf {D} +\mathbf {B} \cdot \mathbf {H} \right)\quad {\hbox{with}}\quad \mathbf {D} \equiv \epsilon _{0}\mathbf {E} \quad {\hbox{and}}\quad \mathbf {B} \equiv \mu _{0}\mathbf {H}$

and

$\mathbf {P} \equiv {\frac {1}{\mu _{0}}}\mathbf {E} \times \mathbf {B} =\mathbf {E} \times \mathbf {H}$

where P is the Poynting vector called after John Henry Poynting, then

${\mathcal {E}}_{\textrm {Joule}}=-{\frac {\partial {\mathcal {E}}_{\textrm {Field}}}{\partial t}}-{\boldsymbol {\nabla }}\cdot \mathbf {P} .$

The divergence of the Poynting vector is the energy flow associated with the electromagnetic wave, i.e., with the pair E(r,t) and B(r,t). By definition ∇·P gives the flow leaving the system and − ∇·P gives the flow entering the system.

Here we have found an example of the conservation of energy, known as Poynting's theorem: The energy transported from the system to the environment per unit time according to Joule's law $\scriptstyle {\mathcal {E}}_{\textrm {Joule}}$ is equal to the rate in decrease of the electromagnetic energy of the system $\scriptstyle {\mathcal {E}}_{\textrm {Field}}$, which is compensated by the flow of EM radiation ∇·P entering the system.

If there is no current, J = 0, then

${\frac {\partial {\mathcal {E}}_{\textrm {Field}}}{\partial t}}=-{\boldsymbol {\nabla }}\cdot \mathbf {P} ,$

which is the continuity equation. The increase of field energy per unit time is the flow of radiation energy into the system.

(To be continued)

External link

ISO 21348 Definitions of Solar Irradiance Spectral Categories

To be continued