Archive:New Draft of the Week
The New Draft of the Week is a chance to highlight a recently created Citizendium article that has just started down the road of becoming a Citizendium masterpiece.
It is chosen each week by vote in a manner similar to that of its sister project, the Article of the Week.
Add New Nominees Here
To add a new nominee or vote for an existing nominee, click edit for this section and follow the instructions
| Nominated article | Vote Score |
Supporters | Specialist supporters | Date created |
|---|---|---|---|---|
| 1 | Milton Beychok; | 2009-06-27 | ||
| 2 | Milton Beychok; Meg Ireland; | 2009-07-10 |
If you want to see how these nominees will look on the CZ home page (if selected as a winner), scroll down a little bit.
Transclusion of the above nominees (to be done by an Administrator)
- Transclude each of the nominees in the above "Table of Nominee" as per the instructions at Template:Featured Article Candidate.
- Then add the transcluded article to the list in the next section below, using the {{Featured Article Candidate}} template.
View Current Transcluded Nominees (after they have been transcluded by an Administrator)
The next New Draft of the Week will be the article with the most votes at 1 AM UTC on Thursday, 16 July 2009. I did the honors this time. Milton Beychok 01:11, 16 July 2009 (UTC)
| Nominated article | Supporters | Specialist supporters | Dates | Score | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
The Clean Air Act is a law enacted by the U.S. Congress that defines the responsibilities of the U.S. Environmental Protection Agency (U.S. EPA) for protecting and improving the nation's air quality and the stratospheric ozone layer. The latest major amendments were enacted as the Clean Air Act Amendments of 1990 (Public Law 101–549). The Clean Air Act Amendments of 1990 were preceded by various other pieces of legislation enacted by the U.S. Congress dating back to the Air Pollution Control Act of 1955.
Implementation of the ActIn the same year that Congress created the Clean Air Act of 1970 (see History section below), Congress also created the U.S. EPA and gave it the primary role in carrying out the law. Since 1970, the U.S. EPA has been responsible for a variety of programs to reduce air pollution nationwide. However, the environmental regulatory agencies of the states, Indian tribes and local governments do a lot of the work to meet the Act's requirements. Those agencies work with industrial and commercial companies to reduce air pollution. They also review and approve permit applications for construction and operation of industrial plants and commercial facilities involving sources of air pollution. They are able to develop solutions for pollution problems that require special understanding of local industries, geography, housing, and travel patterns, as well as other factors. State, local, and tribal governments also monitor air quality, inspect facilities under their jurisdictions and enforce Clean Air Act regulations.[1] States must also develop State Implementation Plans (SIPs) that outline how each state will control air pollution under the Clean Air Act. An SIP is a collection of the regulations, programs and policies that a state will use to clean up polluted areas. In developing their SIPs, the states must involve the public and industries through hearings and opportunities to comment on the development of each state plan.[1] Contents of the ActLegislation enacted by the U.S. Congress since 1990 has made several minor changes in the Act. The current version, including amendments through February 24, 2004, is available on the Internet.[2] This is a listing of its major parts:
Key elements of the actThe U.S. EPA's mission is to protect human health and the environment. To achieve this mission, EPA implemented a variety of programs under the Clean Air Act that focus on:
The above programs have required the development of specific regulations by the U.S. EPA and the state, tribal and local governments to limit the emissions of air pollutants from mobile sources (like automotive vehicles and airplanes) and stationary sources (like petroleum refineries, petrochemical and chemical manufacturing plants, power plants, and gas or petrol stations). More specifics concerning each of the above programs are available on the Internet.[3] What the Clean Air Act has accomplishedThe implementation of the Clean Air Act has accomplished very significant reductions in the emission of air pollutants during the period of 1970 – 2008. The reductions were accomplished despite even larger increases in activities, during that same period, that produce air pollutants as measured by the national Gross Domestic Product (GDP), consumption of energy, and usage of automobiles. The details of that accomplishment are presented in the two tables below:[1][4]
HistoryIn October 1948, a cloud of air pollution formed above the industrial town of Donora, Pennsylvania and lingered for five days. It caused sickness in 6,000 of the town's 14,000 people and the death of 20 people. Four years later, in 1952, over 3,000 people died in what became known as London's "Killer Fog".[1][4] Events like those led to the enactment of several federal and state laws which established funding for the study and the cleanup of air pollution. But there was no comprehensive federal response to address air pollution until Congress passed the Clean Air Act in 1970 and created the U.S. EPA. In 1990, Congress amended and greatly expanded the Clean Air Act, providing EPA even broader authority to implement and enforce regulations reducing air pollutant emissions. The 1990 Amendments also placed an increased emphasis on more cost-effective approaches to reduce air pollution. The principal milestones in the evolution of the Clean Air Act are:[4][5][6] The Air Pollution Control Act of 1955The Air Pollution Control Act of 1955 was the first federal legislation that involved air pollution. It funded research of air pollution and state assistance resources. Clean Air Act of 1963The Clean Air Act of 1963 was the first federal legislation regarding air pollution control. It established a federal program within the U.S. Public Health Service and authorized research into techniques for monitoring and controlling air pollution. It included grants to the states for developing state and local air pollution control programs. In 1966, the Clean Air Act was extended to add the authority for grants to maintain state and local programs rather than just develop them. Air Quality Act of 1967In 1967, an Air Quality Act was enacted in order to expand federal government activities. In accordance with this law, enforcement proceedings were initiated in areas subject to interstate air pollution transport. As part of these proceedings, the federal government for the first time conducted extensive ambient monitoring studies and stationary source inspections. The Air Quality Act of 1967 also authorized expanded studies of air pollutant emission inventories, ambient monitoring techniques, and control techniques. Clean Air Act 1970The enactment of the Clean Air Act of 1970 constituted a major change of the federal government's role in air pollution control. It authorized the development of comprehensive federal and state regulations to limit emissions from stationary industrial sources and from mobile sources. Four major regulatory programs involving stationary sources were initiated:
It also authorized requirements for the control of automotive vehicle emissions (i.e., mobile sources). Furthermore, the authority to enforce air quality standards and air pollution emission controls was substantially expanded. As mentioned above, the EPA was created at about the same time in order to implement the various requirements included in the Clean Air Act of 1970. 1977 Amendments to the Clean Air Act of 1970The 1977 Amendments established major review requirements to ensure the attainment and maintenance of the National Ambient Air Quality Standards. It codified provisions for the Prevention of Significant Deterioration (PSD) program. It also codified requirements pertaining to air pollution sources in geographical areas called "non-attainment areas" because they had not attained on or more of the National Ambient Air Quality Standards. 1990 Amendments to the Clean Air Act of 1970Another set of major amendments to the Clean Air Act were enacted in 1990 that substantially increased the authority and responsibility of the federal government. New regulatory programs were authorized for:
The provisions for attainment and maintenance of the National Ambient Air Quality Standards were significantly modified and expanded. Other revisions involved stratospheric ozone protection, increased enforcement authority, and expanded research programs. References
|
Milton Beychok; | 1
| ||||||||||||||||||||||||||
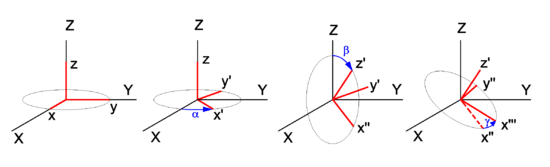
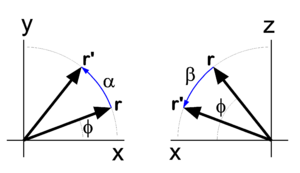
In physics, mathematics, and engineering, Euler angles are three rotation angles, often denoted by 0 ≤ α ≤ 2π, 0 ≤ β ≤ π, and 0 ≤ γ ≤ 2π, although the notation φ, θ, ψ is also common. Any rotation of a 3-dimensional object can be performed by three consecutive rotations over the three Euler angles. Different conventions are in use: a rotation can be active (the object is rotated, the system of axes is fixed in space), or passive (the object is fixed in space, the axes are rotated). Also the choice of rotation axes may vary; an active convention common in quantum mechanical applications is the z-y′-z′ convention. Attach a system of Cartesian coordinate axes to the body that is to be rotated (the coordinate frame is fixed to the body and is rotated simultaneously with it); in the figure the body-fixed frame is shown in red and labeled by lowercase letters. First rotate around z, then around the new body-fixed y-axis, y′, and finally around z′. Another convention often used is the z-x′-z′ convention, where instead of over the new y-axis the second rotation is over the new x-axis. Also the z-y-x convention is used (and will be discussed below). The right-hand screw rule is practically always followed: the rotation axis is a directed line and a positive rotation is as a cork screw driven into the positive direction of the axis. In older literature left-handed Cartesian coordinate frames appear sometimes, but in modern literature right-handed frames are used exclusively. Euler angles are used in many different branches of physics and engineering. The present article is written from the point of view of molecular physics, where the objects to be rotated are molecules and applications are often of quantum mechanical nature. The angles are named after the 18th century mathematician Leonhard Euler who introduced in 1765 two of the three for an axially symmetric body where the third angle, γ, does not play a role.[1] Geometric discussionIn Figure 1 the space-fixed (laboratory) axes are labeled by capital X, Y, and Z and are shown in black. The body to be rotated is not shown, but a system of axes fixed to it is shown in red. One may use any convenient orthonormal frame as a body-fixed frame. Often the body-fixed axes are principal axes, that means that they are eigenvectors of the inertia tensor of the body. Also symmetry axes, when present, may be used. When the body has symmetry axes, the principal axes often coincide with these. The z-y′-z′ convention will be followed. Initially, the two frames coincide, and the path to a final arbitrary orientation of the body—and its frame—is depicted on Figure 1. The first rotation is around the z-axis, which coincides with the Z-axis. The x- and y-axis move in a plane perpendicular to the z-axis over an angle α. The second rotation is in a plane through the origin perpendicular to the y′-axis. The angle is β. The present convention has the practical advantage that the z′-axis has the usual spherical polar coordinates α ≡ φ (longitude angle) and β ≡ θ (colatitude angle) with respect to the space-fixed frame.[2] The final rotation is in a plane perpendicular to the z′-axis over an angle γ. From geometric considerations follows that any orientation of the body-fixed frame in space may be obtained. Write for the rotation matrix that describes a rotation around the unit vector over an angle . Clearly the three consecutive Euler rotations correspond to rotations around the unit vectors along the body-fixed axes z, y′, and z′ over angles α β, and γ, respectively. Because a matrix acts on a column vector to its right, the order in the matrix product is as in the leftmost term in the following equation. It will be shown that the corresponding matrix product can be written in reverse order (but around fixed, unprimed, axes z, y, z), that is, Note that the third column contains the Cartesian coordinates with respect to the space-fixed frame of expressed in sines and cosines of spherical polar angles. The first and second column contain by definition expressions for the Cartesian coordinates of and , respectively, but evidently these are not solely in terms of spherical polar angles, γ also enters. Before proving the first equality in the above equation (reversal of order), we derive the matrix for a rotation around the z-axis, see the left drawing in Figure 2. The rotated vector has components We used here the relations well-known from trigonometry for the sine and cosine of a sum angle. The derivation of the matrix for a rotation around the y-axis proceeds along the same lines. Note, however, that the angle of a vector with the x-axis decreases by a rotation around the positive y-axis (see right-hand drawing in Figure 2). To prove the first equality (reversal of the order in the angles), a property of rotation matrices is used. A rotation (orthogonal 3×3) matrix A, transforming a rotation axis, gives rise to the following similarity equation, where the superscript T indicates the transpose of the matrix. For rotation matrices the transposed matrix is equal to the inverse of the matrix. From this similarity relation follows that so that Also so that where it is used that rotations around the same axis commute, that is, and the required result is proved. Algebraic treatmentIn the proof that any rotation can be written as three consecutive rotations, an appeal was made to the geometric insight of the reader. The same result can be proved more rigorously by algebraic means. To that end the notation is somewhat shortened: TheoremA proper rotation matrix R can be factorized thus which is referred to as the Euler z-y-x parametrization, or also as the Euler z-y-z parametrization. ProofFirst the Euler z-y-x-parametrization will be proved by an algorithm for the factorization of a given matrix R ≡ (r1, r2, r3). Second the z-y-z parametrization will be proved; this parametrization is—as shown above—equivalent to the z′-y′-z parametrization with angles in reverse order. :A Fortran subroutine based on the algorithm is given on the code page. To prove the z-y-x parametrization we consider the matrix product The columns of the matrix product are for ease of reference designated by a1, a2, and a3. Note that the multiplication by on the right does not affect the first column, so that a1 = r1 (the first column of R). Solve and from the first column of R (which is known), This is possible. First solve for from Then solve for from the two equations: The angles and determine fully the vectors a2 and a3. Since a1, a2 and a3 are the columns of a proper rotation matrix they form an orthonormal right-handed system. The plane spanned by a2 and a3 is orthogonal to and hence the plane contains and . Thus the latter two vectors are a linear combination of the first two, Since are known orthonormal vectors, we can compute These equations give with . The angle ω1 gives the matrix with This gives the required z-y-x factorization of the arbitrary proper orthogonal matrix R. The proof of the Euler z-y-z parametrization is obtained by a small modification of the previous proof. We start by retrieving the spherical polar coordinates and of the unit vector , the third column [the rightmost multiplication by Rz(ω1) does not affect r3]. Then consider or, The equation for R can be written as which proves the Euler z-y-z parametrization. Clearly, this factorization is equal to the one given in the previous section, with Note
|
Milton Beychok; Meg Ireland | 2
|
Current Winner (to be selected and implemented by an Administrator)
To change, click edit and follow the instructions, or see documentation at {{Featured Article}}.
| The metadata subpage is missing. You can start it via filling in this form or by following the instructions that come up after clicking on the [show] link to the right. | |||
|---|---|---|---|
|
Heat is a form of energy that is transferred between two bodies that are in thermal contact and have different temperatures. For instance, the bodies may be two compartments of a vessel separated by a heat-conducting wall and containing fluids of different temperatures on either side of the wall. Or one body may consist of hot radiating gas and the other may be a kettle with cold water, as shown in the picture. Heat flows spontaneously from the higher-temperature to the lower-temperature body. The effect of this transfer of energy usually, but not always, is an increase in the temperature of the colder body and a decrease in the temperature of the hotter body.
Change of aggregation state
A vessel containing a fluid may lose or gain energy without a change in temperature when the fluid changes from one aggregation state to another. For instance, a gas condensing to a liquid does this at a certain fixed temperature (the boiling point of the liquid) and releases condensation energy. When a vessel, containing a condensing gas, loses heat to a colder body, then, as long as there is still vapor left in it, its temperature remains constant at the boiling point of the liquid, even while it is losing heat to the colder body. In a similar way, when the colder body is a vessel containing a melting solid, its temperature will remain constant while it is receiving heat from a hotter body, as long as not all solid has been molten. Only after all of the solid has been molten and the heat transport continues, the temperature of the colder body (then containing only liquid) will rise.
For example, the temperature of the tap water in the kettle shown in the figure will rise quickly to the boiling point of water (100 °C). Then, when the flame is not switched off, the temperature inside the kettle remains constant at 100 °C for quite some time, even though heat keeps on flowing from flame to kettle. When all liquid water has evaporated—when the kettle has boiled dry—the temperature of the kettle will quickly rise again until it obtains the temperature of the burning gas, then the heat flow will finally stop. (Most likely, though, the handle and maybe the metal of the kettle, too, will have melted before that).
Units
At present the unit for the amount of heat is the same as for any form of energy. Before the equivalence of mechanical work and heat was clearly recognized, two units were used. The calorie was the amount of heat necessary to raise the temperature of one gram of water from 14.5 to 15.5 °C and the unit of mechanical work was basically defined by force times path length (in the old cgs system of units this is erg). Now there is one unit for all forms of energy, including heat. In the International System of Units (SI) it is the joule, but the British Thermal Unit and calorie are still occasionally used. The unit for the rate of heat transfer is the watt (J/s).
Equivalence of heat and work
Although heat and work are forms of energy that both obey the law of conservation of energy, they are not completely equivalent. Work can be completely converted into heat, but the converse is not true. When converting heat into work, part of the heat is not—and cannot be—converted to work, but flows to the body of lower temperature that is out of necessity present to generate a heat flow.
Heat and temperature
The important distinction between heat and temperature (heat being a form of energy and temperature a measure of the amount of that energy present in a body) was clarified by Count Rumford, James Prescott Joule, Julius Robert Mayer, Rudolf Clausius, and others during the late 18th and 19th centuries. Also it became clear by the work of these men that heat is not an invisible and weightless fluid, named caloric, as was thought by many 18th century scientists, but a form of motion. The molecules of the hotter body are (on the average) in more rapid motion than those of the colder body. The first law of thermodynamics, discovered around the middle of the 19th century, states that the (flow of) heat is a transfer of part of the internal energy of the bodies. In the case of ideal gases, internal energy consists only of kinetic energy and it is indeed only this motional energy that is transferred when heat is exchanged between two containers with ideal gases. In the case of non-ideal gases, liquids and solids, internal energy also contains the averaged inter-particle potential energy (attraction and repulsion between molecules), which depends on temperature. So, for non-ideal gases, liquids and solids, also potential energy is transferred when heat transfer occurs.
Forms of heat
The actual transport of heat may proceed by electromagnetic radiation (as an example one may think of an electric heater where usually heat is transferred to its surroundings by infrared radiation, or of a microwave oven where heat is given off to food by microwaves), conduction (for instance through a metal wall; metals conduct heat by the aid of their almost free electrons), and convection (for instance by air flow or water circulation).
Entropy
If two systems, 1 (cold) and 2 (hot), are isolated from the rest of the universe (i.e., no other heat flows than from 2 to 1 and no work is performed on the two systems) then the entropy Stot = S1 + S2 of the total system 1 + 2 increases upon the spontaneous flow of heat. This is in accordance with the second law of thermodynamics that states that spontaneous thermodynamic processes are associated with entropy increase. In general, the entropy S of a system at absolute temperature T increases with
when it receives an amount of heat Q > 0. Entropy is an additive (size-extensive) property.
The hotter system 2 loses an amount of heat to the colder system 1. In absolute value the exchanged amounts of heat are the same by the law of conservation of energy (no energy escapes to the rest of the universe), hence
Here it is assumed that the amount of heat Q is so small that the temperatures of the two systems are constant. One can achieve this by considering a small time interval of heat exchange and/or very large systems.
Remark: the expression ΔS = Q/T is only strictly valid for a reversible (also known as quasistatic) flow of energy. It is possible[1] to define:
It is assumed that ΔSint is much smaller than ΔSext, so that it can be neglected.
Semantic caveats
It is strictly speaking not correct to say that a hot object "possesses much heat"—it is correct to say, however, that it possesses high internal energy. The word "heat" is reserved to describe the process of transfer of energy from a high temperature object to a lower temperature one (in short called "heating of the cold object"). The reason that the word "heat" is to be avoided for the internal energy of an object is that the latter can have been acquired either by heating or by work done on it (or by both). When we measure internal energy, there is no way of deciding how the object acquired it—by work or by heat. In the same way as one does not say that a hot object "possesses much work", one does not say that it "possesses much heat". Yet, terms as "heat reservoir" (a system of temperature higher than its environment that for all practical purposes is infinite) and "heat content" (a synonym for enthalpy) are commonly used and are incorrect by the same reasoning.
The molecules of a hot body are in agitated motion and, as said, it cannot be measured how they became agitated, by work or by heat. Often, especially outside physics, the random molecular motion is referred to as "thermal energy". In classical (phenomenological) thermodynamics this is an intuitive, but undefined, concept. In statistical thermodynamics, thermal energy could be defined (but rarely ever is) as the average kinetic energy of the molecules constituting the body. Kinetic and potential energy of molecules are concepts that are foreign to classical thermodynamics, which predates the general acceptance of the existence of molecules.
Quotation
As a result Carathéodory was able to obtain the laws of thermodynamics without recourse to fictitious machines or objectionable concepts as the flow of heat.[2]
Reference
Previous Winners
 Continuum hypothesis: A statement about the size of the continuum, i.e., the number of elements in the set of real numbers. [e] (July 9)
Continuum hypothesis: A statement about the size of the continuum, i.e., the number of elements in the set of real numbers. [e] (July 9) Hawaiian alphabet: The form of writing used in the Hawaiian Language [e] (July 2)
Hawaiian alphabet: The form of writing used in the Hawaiian Language [e] (July 2) Now and Zen: A 1988 studio album recorded by Robert Plant, with guest contributions from Jimmy Page. [e] (June 25)
Now and Zen: A 1988 studio album recorded by Robert Plant, with guest contributions from Jimmy Page. [e] (June 25) Wrench (tool): A fastening tool used to tighten or loosen threaded fasteners, with one end that makes firm contact with flat surfaces of the fastener, and the other end providing a means of applying force [e] (June 18)
Wrench (tool): A fastening tool used to tighten or loosen threaded fasteners, with one end that makes firm contact with flat surfaces of the fastener, and the other end providing a means of applying force [e] (June 18) Air preheater: A general term to describe any device designed to preheat the combustion air used in a fuel-burning furnace for the purpose of increasing the thermal efficiency of the furnace. [e] (June 11)
Air preheater: A general term to describe any device designed to preheat the combustion air used in a fuel-burning furnace for the purpose of increasing the thermal efficiency of the furnace. [e] (June 11) 2009 H1N1 influenza virus: A contagious influenza A virus discovered in April 2009, commonly known as swine flu. [e] (June 4)
2009 H1N1 influenza virus: A contagious influenza A virus discovered in April 2009, commonly known as swine flu. [e] (June 4) Gasoline: A fuel for spark-ignited internal combustion engines derived from petroleum crude oil. [e] (21 May)
Gasoline: A fuel for spark-ignited internal combustion engines derived from petroleum crude oil. [e] (21 May) John Brock: Fictional British secret agent who starred in three 1960s thrillers by Desmond Skirrow. [e] (8 May)
John Brock: Fictional British secret agent who starred in three 1960s thrillers by Desmond Skirrow. [e] (8 May) McGuffey Readers: A set of highly influential school textbooks used in the 19th and early 20th centuries in the elementary grades in the United States. [e] (14 Apr)
McGuffey Readers: A set of highly influential school textbooks used in the 19th and early 20th centuries in the elementary grades in the United States. [e] (14 Apr) Vector rotation: Process of rotating one unit vector into a second unit vector. [e] (7 Apr)
Vector rotation: Process of rotating one unit vector into a second unit vector. [e] (7 Apr) Leptin: Hormone secreted by adipocytes that regulates appetite. [e] (31 Mar)
Leptin: Hormone secreted by adipocytes that regulates appetite. [e] (31 Mar) Kansas v. Crane: A 2002 decision of the Supreme Court of the United States, ruling that a person could not be adjudicated a sexual predator and put in indefinite medical confinement, purely on assessment of an emotional disorder, but such action required proof of a likelihood of uncontrollable impulse presenting a clear and present danger. [e] (24 Mar)
Kansas v. Crane: A 2002 decision of the Supreme Court of the United States, ruling that a person could not be adjudicated a sexual predator and put in indefinite medical confinement, purely on assessment of an emotional disorder, but such action required proof of a likelihood of uncontrollable impulse presenting a clear and present danger. [e] (24 Mar) Punch card: A term for cards used for storing information. Herman Hollerith is credited with the invention of the media for storing information from the United States Census of 1890. [e] (17 Mar)
Punch card: A term for cards used for storing information. Herman Hollerith is credited with the invention of the media for storing information from the United States Census of 1890. [e] (17 Mar) Jass–Belote card games: A group of trick-taking card games in which the Jack and Nine of trumps are the highest trumps. [e] (10 Mar)
Jass–Belote card games: A group of trick-taking card games in which the Jack and Nine of trumps are the highest trumps. [e] (10 Mar) Leptotes (orchid): A genus of orchids formed by nine small species that exist primarily in the dry jungles of South and Southeast Brazil. [e] (3 Mar)
Leptotes (orchid): A genus of orchids formed by nine small species that exist primarily in the dry jungles of South and Southeast Brazil. [e] (3 Mar) Worm (computers): A form of malware that can spread, among networked computers, without human interaction. [e] (24 Feb)
Worm (computers): A form of malware that can spread, among networked computers, without human interaction. [e] (24 Feb) Joseph Black: (1728 – 1799) Scottish physicist and chemist, known for his discoveries of latent heat, specific heat, and carbon dioxide [e] (11 Feb 2009)
Joseph Black: (1728 – 1799) Scottish physicist and chemist, known for his discoveries of latent heat, specific heat, and carbon dioxide [e] (11 Feb 2009) Sympathetic magic: The cultural concept that a symbol, or small aspect, of a more powerful entity can, as desired by the user, invoke or compel that entity [e] (17 Jan 2009)
Sympathetic magic: The cultural concept that a symbol, or small aspect, of a more powerful entity can, as desired by the user, invoke or compel that entity [e] (17 Jan 2009) Dien Bien Phu: Site in northern Vietnam of a 1954 decisive battle that soon forced France to relinquish control of colonial Indochina. [e] (25 Dec)
Dien Bien Phu: Site in northern Vietnam of a 1954 decisive battle that soon forced France to relinquish control of colonial Indochina. [e] (25 Dec) Blade Runner: 1982 science fiction film directed by Ridley Scott and starring Harrison Ford, set in an imagined Los Angeles of 2019. [e] (25 Nov)
Blade Runner: 1982 science fiction film directed by Ridley Scott and starring Harrison Ford, set in an imagined Los Angeles of 2019. [e] (25 Nov) Piquet: A two-handed card game played with 32 cards that originated in France around 1500. [e] (18 Nov)
Piquet: A two-handed card game played with 32 cards that originated in France around 1500. [e] (18 Nov) Crash of 2008: the international banking crisis that followed the subprime mortgage crisis of 2007. [e] (23 Oct)
Crash of 2008: the international banking crisis that followed the subprime mortgage crisis of 2007. [e] (23 Oct) Information Management: The application of management principles to the acquisition, organization, control, dissemination and use of information relevant to the effective operation of organizations of all kinds. [e] (31 Aug)
Information Management: The application of management principles to the acquisition, organization, control, dissemination and use of information relevant to the effective operation of organizations of all kinds. [e] (31 Aug) Battle of Gettysburg: A turning point in the American Civil War, July 1-3, 1863, on the outskirts of Gettysburg, Pennsylvania. [e] (8 July)
Battle of Gettysburg: A turning point in the American Civil War, July 1-3, 1863, on the outskirts of Gettysburg, Pennsylvania. [e] (8 July) Drugs banned from the Olympics: Substances prohibited for use by athletes prior to, and during competing in the Olympics. [e] (1 July)
Drugs banned from the Olympics: Substances prohibited for use by athletes prior to, and during competing in the Olympics. [e] (1 July) Sea glass: Formed when broken pieces of glass from bottles, tableware, and other items that have been lost or discarded are worn down and rounded by tumbling in the waves along the shores of oceans and large lakes. [e] (24 June)
Sea glass: Formed when broken pieces of glass from bottles, tableware, and other items that have been lost or discarded are worn down and rounded by tumbling in the waves along the shores of oceans and large lakes. [e] (24 June) Dazed and Confused (Led Zeppelin song): Landmark 1969 song recorded by Led Zeppelin for their eponymous debut album, which became an early centrepiece for the group's live performances. [e] (17 June)
Dazed and Confused (Led Zeppelin song): Landmark 1969 song recorded by Led Zeppelin for their eponymous debut album, which became an early centrepiece for the group's live performances. [e] (17 June) Hirohito: The 124th and longest-reigning Emperor of Japan, 1926-89. [e] (10 June)
Hirohito: The 124th and longest-reigning Emperor of Japan, 1926-89. [e] (10 June) Henry Kissinger: (1923—) American academic, diplomat, and simultaneously Assistant to the President for National Security Affairs and Secretary of State in the Nixon Administration; promoted realism (foreign policy) and détente with China and the Soviet Union; shared 1973 Nobel Peace Prize for ending the Vietnam War; Director, Atlantic Council [e] (3 June)
Henry Kissinger: (1923—) American academic, diplomat, and simultaneously Assistant to the President for National Security Affairs and Secretary of State in the Nixon Administration; promoted realism (foreign policy) and détente with China and the Soviet Union; shared 1973 Nobel Peace Prize for ending the Vietnam War; Director, Atlantic Council [e] (3 June) Palatalization: An umbrella term for several processes of assimilation in phonetics and phonology, by which the articulation of a consonant is changed under the influence of a preceding or following front vowel or a palatal or palatalized consonant. [e] (27 May)
Palatalization: An umbrella term for several processes of assimilation in phonetics and phonology, by which the articulation of a consonant is changed under the influence of a preceding or following front vowel or a palatal or palatalized consonant. [e] (27 May) Intelligence on the Korean War: The collection and analysis, primarily by the United States with South Korean help, of information that predicted the 1950 invasion of South Korea, and the plans and capabilities of the enemy once the war had started [e] (20 May)
Intelligence on the Korean War: The collection and analysis, primarily by the United States with South Korean help, of information that predicted the 1950 invasion of South Korea, and the plans and capabilities of the enemy once the war had started [e] (20 May) Trinity United Church of Christ, Chicago: A predominantly black church located in south Chicago with upwards of 10,000 members, established in 1961. [e] (13 May)
Trinity United Church of Christ, Chicago: A predominantly black church located in south Chicago with upwards of 10,000 members, established in 1961. [e] (13 May) BIOS: Part of many modern computers responsible for basic functions such as controlling the keyboard or booting up an operating system. [e] (6 May)
BIOS: Part of many modern computers responsible for basic functions such as controlling the keyboard or booting up an operating system. [e] (6 May) Miniature Fox Terrier: A small Australian vermin-routing terrier, developed from 19th Century Fox Terriers and Fox Terrier types. [e] (23 April)
Miniature Fox Terrier: A small Australian vermin-routing terrier, developed from 19th Century Fox Terriers and Fox Terrier types. [e] (23 April) Joseph II: (1741–1790), Holy Roman Emperor and ruler of the Hapsburg (Austrian) territories who was the arch-embodiment of the Enlightenment spirit of the later 18th-century reforming monarchs. [e] (15 Apr)
Joseph II: (1741–1790), Holy Roman Emperor and ruler of the Hapsburg (Austrian) territories who was the arch-embodiment of the Enlightenment spirit of the later 18th-century reforming monarchs. [e] (15 Apr) British and American English: A comparison between these two language variants in terms of vocabulary, spelling and pronunciation. [e] (7 Apr)
British and American English: A comparison between these two language variants in terms of vocabulary, spelling and pronunciation. [e] (7 Apr) Count Rumford: (1753–1814) An American born soldier, statesman, scientist, inventor and social reformer. [e] (1 April)
Count Rumford: (1753–1814) An American born soldier, statesman, scientist, inventor and social reformer. [e] (1 April) Whale meat: The edible flesh of various species of whale. [e] (25 March)
Whale meat: The edible flesh of various species of whale. [e] (25 March) Naval guns: Artillery weapons on ships, and techniques and devices for aiming them. [e] (18 March)
Naval guns: Artillery weapons on ships, and techniques and devices for aiming them. [e] (18 March) Sri Lanka: An island nation in South Asia, located 31 km off the south-east coast of India, formerly known as Ceylon . [e] (11 March)
Sri Lanka: An island nation in South Asia, located 31 km off the south-east coast of India, formerly known as Ceylon . [e] (11 March) Led Zeppelin: English hard rock and blues group formed in 1968, known for their albums and stage shows. [e] (4 March)
Led Zeppelin: English hard rock and blues group formed in 1968, known for their albums and stage shows. [e] (4 March) Martin Luther: German theologian and monk (1483-1546); led the Reformation; believed that salvation is granted on the basis of faith rather than deeds. [e] (20 February)
Martin Luther: German theologian and monk (1483-1546); led the Reformation; believed that salvation is granted on the basis of faith rather than deeds. [e] (20 February) Cosmology: Add brief definition or description (4 February)
Cosmology: Add brief definition or description (4 February) Ernest Rutherford: Add brief definition or description(28 January)
Ernest Rutherford: Add brief definition or description(28 January) Edinburgh: Add brief definition or description (21 January)
Edinburgh: Add brief definition or description (21 January) Russian Revolution of 1905: Add brief definition or description (8 January 2008)
Russian Revolution of 1905: Add brief definition or description (8 January 2008) Phosphorus: Add brief definition or description (31 December)
Phosphorus: Add brief definition or description (31 December) John Tyler: Add brief definition or description (6 December)
John Tyler: Add brief definition or description (6 December) Banana: Add brief definition or description (22 November)
Banana: Add brief definition or description (22 November) Augustin-Louis Cauchy: Add brief definition or description (15 November)
Augustin-Louis Cauchy: Add brief definition or description (15 November)- B-17: Add brief definition or description - 8 November 2007
 Red Sea Urchin: Add brief definition or description - 1 November 2007
Red Sea Urchin: Add brief definition or description - 1 November 2007 Symphony: Add brief definition or description - 25 October 2007
Symphony: Add brief definition or description - 25 October 2007 Oxygen: Add brief definition or description - 18 October 2007
Oxygen: Add brief definition or description - 18 October 2007 Origins and architecture of the Taj Mahal: Add brief definition or description - 11 October 2007
Origins and architecture of the Taj Mahal: Add brief definition or description - 11 October 2007 Fossilization (palaeontology): Add brief definition or description - 4 October 2007
Fossilization (palaeontology): Add brief definition or description - 4 October 2007 Cradle of Humankind: Add brief definition or description - 27 September 2007
Cradle of Humankind: Add brief definition or description - 27 September 2007 John Adams: Add brief definition or description - 20 September 2007
John Adams: Add brief definition or description - 20 September 2007 Quakers: Add brief definition or description - 13 September 2007
Quakers: Add brief definition or description - 13 September 2007 Scarborough Castle: Add brief definition or description - 6 September 2007
Scarborough Castle: Add brief definition or description - 6 September 2007 Jane Addams: Add brief definition or description - 30 August 2007
Jane Addams: Add brief definition or description - 30 August 2007 Epidemiology: Add brief definition or description - 23 August 2007
Epidemiology: Add brief definition or description - 23 August 2007 Gay community: Add brief definition or description - 16 August 2007
Gay community: Add brief definition or description - 16 August 2007 Edward I: Add brief definition or description - 9 August 2007
Edward I: Add brief definition or description - 9 August 2007
Rules and Procedure
Rules
- The primary criterion of eligibility for a new draft is that it must have been ranked as a status 1 or 2 (developed or developing), as documented in the History of the article's Metadate template, no more than one month before the date of the next selection (currently every Thursday).
- Any Citizen may nominate a draft.
- No Citizen may have nominated more than one article listed under "current nominees" at a time.
- The article's nominator is indicated simply by the first name in the list of votes (see below).
- At least for now--while the project is still small--you may nominate and vote for drafts of which you are a main author.
- An article can be the New Draft of the Week only once. Nominated articles that have won this honor should be removed from the list and added to the list of previous winners.
- Comments on nominations should be made on the article's talk page.
- Any draft will be deleted when it is past its "last date eligible". Don't worry if this happens to your article; consider nominating it as the Article of the Week.
- If an editor believes that a nominee in his or her area of expertise is ineligible (perhaps due to obvious and embarrassing problems) he or she may remove the draft from consideration. The editor must indicate the reasons why he has done so on the nominated article's talk page.
Nomination
See above section "Add New Nominees Here".
Voting
- To vote, add your name and date in the Supporters column next to an article title, after other supporters for that article, by signing
<br />~~~~. (The date is necessary so that we can determine when the last vote was added.) Your vote is alloted a score of 1. - Add your name in the Specialist supporters column only if you are an editor who is an expert about the topic in question. Your vote is alloted a score of 1 for articles that you created and 2 for articles that you did not create.
- You may vote for as many articles as you wish, and each vote counts separately, but you can only nominate one at a time; see above. You could, theoretically, vote for every nominated article on the page, but this would be pointless.
Ranking
- The list of articles is sorted by number of votes first, then alphabetically.
- Admins should make sure that the votes are correctly tallied, but anyone may do this. Note that "Specialist Votes" are worth 3 points.
Updating
- Each Thursday, one of the admins listed below should move the winning article to the Current Winner section of this page, announce the winner on Citizendium-L and update the "previous winning drafts" section accordingly.
- The winning article will be the article at the top of the list (ie the one with the most votes).
- In the event of two or more having the same number of votes :
- The article with the most specialist supporters is used. Should this fail to produce a winner, the article appearing first by English alphabetical order is used.
- The remaining winning articles are guaranteed this position in the following weeks, again in alphabetical order. No further voting should take place on these, which remain at the top of the table with notices to that effect. Further nominations and voting take place to determine future winning articles for the following weeks.
- Winning articles may be named New Draft of the Week beyond their last eligible date if their circumstances are so described above.
- The article with the most specialist supporters is used. Should this fail to produce a winner, the article appearing first by English alphabetical order is used.
Administrators
The Administrators of this program are the same as the admins for CZ:Article of the Week.
References
See Also
- CZ:Article of the Week
- CZ:Markup tags for partial transclusion of selected text in an article
- CZ:Monthly Write-a-Thon