Affine space: Difference between revisions
imported>Paul Wormer No edit summary |
imported>Paul Wormer No edit summary |
||
| Line 1: | Line 1: | ||
{{subpages}} | {{subpages}} | ||
The 2-dimensional plane | The 2-dimensional plane, well-known from [[Euclidean geometry|elementary Euclidean geometry]], is an example of an '''affine space'''. | ||
From elementary geometry we know that any two points | From elementary geometry we know that any two points in a plane (a collection of infinitely many points) can be connected by a line segment. If the points ''P'' and ''Q'' in a plane are [[ordered pair|ordered]] with ''P'' before ''Q'', the line segment connecting the two becomes an ''arrow'' pointing from ''P'' to ''Q''. This arrow can be mapped onto a [[vector]], the ''difference vector'', denoted by <font style = "vertical-align: 20%"><math>\overrightarrow{PQ}</math></font>.<ref> Sometimes it is stated: "the arrow is a vector", but in the present context it is necessary to carefully distinguish arrows from vectors.</ref> If all arrows in a plane can be mapped onto vectors of a ''2''-dimensional [[vector space]] ''V''<sub>''2''</sub>, called the ''difference space'', the plane is an <b>affine space of dimension ''2''</b>, denoted by ''A''<sub>2</sub>. | ||
Arrows that are mapped onto the same vector in the difference space are said to be ''parallel'', they differ from each other by [[translation]]. | Arrows that are mapped onto the same vector in the difference space are said to be ''parallel'', they differ from each other by [[translation]]. | ||
In elementary | In elementary geometry, the map of arrows onto vectors is almost always defined by the choice of an origin ''O'', which is a point somewhere in the plane. Clearly, an arbitrary point ''P'' is the head of an arrow with tail in the origin and corresponding with the unique difference vector <font style = "vertical-align: 20%"><math>\overrightarrow{OP}</math></font>. All arrows with tail in ''O'' are mapped one-to-one onto a 2-dimensional difference space ''V''<sub>''2''</sub>, with the vector addition in ''V''<sub>''2''</sub> in one-to-one correspondence with the parallelogram rule for the addition of arrows in the plane. | ||
Usually one equips the difference space with an inner product, turning | Usually one equips the difference space with an inner product, turning it into an [[inner product space]]. Its elements have well-defined length, namely, the square root of the inner product of the vector with itself. The distance between any two points ''P'' and ''Q'' may now be defined as the length of <font style = "vertical-align: 20%"><math>\overrightarrow{PQ}</math></font> in ''V''<sub>''2''</sub>. | ||
Upon formalizing the definition, we replace the dimension 2 by an arbitrary finite dimension ''n'' and replace arrows by ordered pairs of points ( | Upon formalizing and generalizing the definition of affine space, we replace the dimension 2 by an arbitrary finite dimension ''n'' and replace arrows by ordered pairs of points ("head" and "tail") in a given point space ''A''. Briefly, ''A'' is an affine space of dimension ''n'' if there exists a map of the [[Cartesian product]], ''A'' × ''A'' onto a vector space of dimension ''n''. This map must satisfy certain axioms that are treated in the next section. If the dimension needs to be exhibited, we may write ''A''<sub>''n''</sub> for the affine space of dimension ''n''. | ||
==Formal definition== | ==Formal definition== | ||
| Line 21: | Line 21: | ||
\overrightarrow{PQ} + \overrightarrow{QR} = \overrightarrow{PR}. | \overrightarrow{PQ} + \overrightarrow{QR} = \overrightarrow{PR}. | ||
</math> | </math> | ||
If these three postulates hold, the set ''A'' is | If these three postulates hold, the set ''A'' is <i>an ''n''-dimensional affine space with difference space ''V''</i>. | ||
Two immediate and important consequences are: | |||
:<math> | :<math> | ||
\begin{align} | \begin{align} | ||
| Line 33: | Line 33: | ||
</math> | </math> | ||
'''Lemma:''' | |||
'''Lemma 1:''' | |||
:<math> | :<math> | ||
\overrightarrow{PQ} = \vec{0} \quad \Longleftrightarrow\quad P = Q | \overrightarrow{PQ} = \vec{0} \quad \Longleftrightarrow\quad P = Q | ||
| Line 56: | Line 57: | ||
See the figure for a concrete example in which the four points form a parallelogram. | See the figure for a concrete example in which the four points form a parallelogram. | ||
'''Proof''' Subtract the following equations: | '''Proof:''' Subtract the following equations: | ||
:<math> | :<math> | ||
\begin{align} | \begin{align} | ||
| Line 70: | Line 71: | ||
==Position vector== | ==Position vector== | ||
Choose a fixed point ''O'' in the affine space ''A'', an | Choose a fixed point ''O'' in the affine space ''A'', an ''origin''. Every point ''P'' is uniquely determined by the vector <font style = "vertical-align: 20%"><math> \overrightarrow{OP} \in V</math></font>. Indeed, suppose that there is another point ''Q'' such that <font style = "vertical-align: 15%"><math>\overrightarrow{OP} = \overrightarrow{OQ} </math></font>, it then follows from lemma 1 that ''P'' = ''Q''. | ||
Choice of another | The vector <font style = "vertical-align: 20%"><math>\vec{v}\equiv\overrightarrow{OP}</math></font> is the <i>position vector of ''P'' with respect to ''O''</i>. After choosing ''O'' every point ''P'' in ''A'' is uniquely identified by its corresponding position vector <font style = "vertical-align: 15%"><math>\vec{v} \in V</math></font>. | ||
Choice of another origin ''O'' '''′''' gives a translation of <font style = "vertical-align: 12%"><math>\vec{v}</math></font> by <font style = "vertical-align: 25%"><math>-\vec{t} \equiv -\overrightarrow{OO\;'}</math></font>, for | |||
:<math> | :<math> | ||
\vec{v} \equiv \overrightarrow{OP} = \overrightarrow{OO'}+ \overrightarrow{O'P} = \vec{t} + \vec{v}\;' | \vec{v} \equiv \overrightarrow{OP} = \overrightarrow{OO\;'}+ \overrightarrow{O'P} = \vec{t} + \vec{v}\;' | ||
\quad\Longrightarrow\quad \vec{v}\;' = \vec{v} - \vec{t} | \quad\Longrightarrow\quad \vec{v}\;' = \vec{v} - \vec{t} | ||
</math> | </math> | ||
with <font style = "vertical-align: 15%"><math> \vec{v}\;' </math></font> the position vector of ''P'' with respect to ''O''′. | with <font style = "vertical-align: 15%"><math> \vec{v}\;' </math></font> the position vector of ''P'' with respect to ''O'' '''′'''. | ||
==Affine coordinate system== | |||
An affine coordinate system | |||
:<math> | |||
(O; \,\vec{e}_1, \vec{e}_2,\ldots, \vec{e}_n) | |||
</math> | |||
consists of an origin ''O'' in ''A'' and a [[basis]] <font style = "vertical-align: 10%"><math>\vec{e}_i;\,\, i=1,\ldots,n</math></font> of the difference space ''V''. Then every point ''P'' in ''A'' determines a system of ''n'' real numbers ''x''<sub>''i''</sub> (''i'' = 1, ..., ''n'') by | |||
:<math> | |||
\overrightarrow{OP} = \sum_{i=1}^n \, x_i\, \vec{e}_i \in V. | |||
</math> | |||
==Notes== | |||
<references /> | |||
Revision as of 10:12, 8 November 2008
The 2-dimensional plane, well-known from elementary Euclidean geometry, is an example of an affine space.
From elementary geometry we know that any two points in a plane (a collection of infinitely many points) can be connected by a line segment. If the points P and Q in a plane are ordered with P before Q, the line segment connecting the two becomes an arrow pointing from P to Q. This arrow can be mapped onto a vector, the difference vector, denoted by .[1] If all arrows in a plane can be mapped onto vectors of a 2-dimensional vector space V2, called the difference space, the plane is an affine space of dimension 2, denoted by A2. Arrows that are mapped onto the same vector in the difference space are said to be parallel, they differ from each other by translation.
In elementary geometry, the map of arrows onto vectors is almost always defined by the choice of an origin O, which is a point somewhere in the plane. Clearly, an arbitrary point P is the head of an arrow with tail in the origin and corresponding with the unique difference vector . All arrows with tail in O are mapped one-to-one onto a 2-dimensional difference space V2, with the vector addition in V2 in one-to-one correspondence with the parallelogram rule for the addition of arrows in the plane.
Usually one equips the difference space with an inner product, turning it into an inner product space. Its elements have well-defined length, namely, the square root of the inner product of the vector with itself. The distance between any two points P and Q may now be defined as the length of in V2.
Upon formalizing and generalizing the definition of affine space, we replace the dimension 2 by an arbitrary finite dimension n and replace arrows by ordered pairs of points ("head" and "tail") in a given point space A. Briefly, A is an affine space of dimension n if there exists a map of the Cartesian product, A × A onto a vector space of dimension n. This map must satisfy certain axioms that are treated in the next section. If the dimension needs to be exhibited, we may write An for the affine space of dimension n.
Formal definition
We will restrict the definition to vector spaces over the field of real numbers.
Let V be an n-dimensional vector space and A a set of elements that we will call points. Assume that a relation between points and vectors is defined in the following way:
- To every ordered pair P, Q of A there is assigned a vector of V, called the difference vector, denoted by .
- To every point P of A and every vector of V there exists exactly one point Q in A, such that .
- If P, Q, and R are three arbitrary points in A, then
If these three postulates hold, the set A is an n-dimensional affine space with difference space V.
Two immediate and important consequences are:
Lemma 1:
- .
Proof: If the points coincide, , we just saw that the difference vector is the zero vector. Conversely, assume that and . Then for an arbitrary point ,
which implies that the same vector in V connects in A with two different points, which by postulate 2 is forbidden.
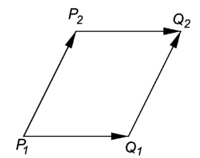
Parallelogram law
Consider four points in A: P1, P2, Q1, and Q2. Assume that the following difference vectors are equal,
then
See the figure for a concrete example in which the four points form a parallelogram.
Proof: Subtract the following equations:
This gives
Position vector
Choose a fixed point O in the affine space A, an origin. Every point P is uniquely determined by the vector . Indeed, suppose that there is another point Q such that , it then follows from lemma 1 that P = Q.
The vector is the position vector of P with respect to O. After choosing O every point P in A is uniquely identified by its corresponding position vector .
Choice of another origin O ′ gives a translation of by , for
with the position vector of P with respect to O ′.
Affine coordinate system
An affine coordinate system
consists of an origin O in A and a basis of the difference space V. Then every point P in A determines a system of n real numbers xi (i = 1, ..., n) by
Notes
- ↑ Sometimes it is stated: "the arrow is a vector", but in the present context it is necessary to carefully distinguish arrows from vectors.