Affine space: Difference between revisions
imported>Paul Wormer |
imported>Paul Wormer |
||
| Line 6: | Line 6: | ||
Usually one takes as a difference space an [[inner product space]]. Its elements have a well-defined length, namely, the square root of the inner product of the vector with itself. The distance between points ''P'' and ''Q'' in an affine space is then defined as the length of the image of <font style = "vertical-align: 20%"><math>\overrightarrow{PQ}</math></font> in ''V''<sub>''n''</sub>. Difference vectors that are mapped onto the same element of ''V''<sub>''n''</sub> are said to be ''parallel'', they differ from each other by [[translation]]. | Usually one takes as a difference space an [[inner product space]]. Its elements have a well-defined length, namely, the square root of the inner product of the vector with itself. The distance between points ''P'' and ''Q'' in an affine space is then defined as the length of the image of <font style = "vertical-align: 20%"><math>\overrightarrow{PQ}</math></font> in ''V''<sub>''n''</sub>. Difference vectors that are mapped onto the same element of ''V''<sub>''n''</sub> are said to be ''parallel'', they differ from each other by [[translation]]. | ||
==Formal definition== | ==Formal definition== | ||
We will restrict the definition to vector | We will restrict the definition to [[vector space]]s over the [[Field theory (mathematics)|field]] <font style = "vertical-align: 10%"><math>\mathbb{R}</math></font> of real numbers. | ||
Let ''V'' be an ''n''-dimensional vector space and ''A'' a set of elements that we will call points. Assume that a relation between points and vectors is defined in the following way: | Let ''V'' be an ''n''-dimensional vector space and ''A'' a set of elements that we will call points. Assume that a relation between points and vectors is defined in the following way: | ||
# To every ordered pair ''P'', ''Q'' of ''A'' there is assigned a vector of ''V'', called the difference vector, denoted by <font style = "vertical-align: 20%"><math>\overrightarrow{PQ} \in V</math></font>. | # To every ordered pair ''P'', ''Q'' of ''A'' there is assigned a vector of ''V'', called the difference vector, denoted by <font style = "vertical-align: 20%"><math>\overrightarrow{PQ} \in V</math></font>. | ||
# To every point ''P'' of ''A'' and every vector <font style = "vertical-align: 15%"><math>\vec{v}</math></font> of ''V'' there exists exactly one point ''Q'' in ''A'', such that <font style = "vertical-align: 15%"><math>\overrightarrow{PQ} = \vec{v}</math></font> | # To every point ''P'' of ''A'' and every vector <font style = "vertical-align: 15%"><math>\vec{v}</math></font> of ''V'' there exists exactly one point ''Q'' in ''A'', such that <font style = "vertical-align: 15%"><math>\overrightarrow{PQ} = \vec{v}</math></font>. | ||
# If ''P'', ''Q'', and ''R'' are three arbitrary points in ''A'', then | # If ''P'', ''Q'', and ''R'' are three arbitrary points in ''A'', then | ||
:::<math> | :::<math> | ||
\overrightarrow{PQ} + \overrightarrow{QR} = \overrightarrow{PR}. | \overrightarrow{PQ} + \overrightarrow{QR} = \overrightarrow{PR}. | ||
</math> | </math> | ||
If these three | If these three postulates hold, the set ''A'' is called an ''n''-dimensional affine space with difference space ''V''. | ||
Immediate consequences: | Immediate consequences: | ||
:<math> | :<math> | ||
\overrightarrow{PP} + \overrightarrow{PR} = \overrightarrow{PR} \quad\Longrightarrow\quad | \begin{align} | ||
\overrightarrow{ | \overrightarrow{PP} + \overrightarrow{PR} &= \overrightarrow{PR} &\Longrightarrow\quad | ||
</math> | \overrightarrow{PP} = \vec{0}.\qquad \\ | ||
\overrightarrow{PQ} + \overrightarrow{QP} &= \vec{0}\qquad &\Longrightarrow\quad | |||
\overrightarrow{PQ} = -\overrightarrow{QP}. \\ | |||
\end{align} | |||
</math> | |||
'''Lemma:''' | |||
:<math> | |||
\overrightarrow{PQ} = \vec{0} \quad \Longleftrightarrow\quad P = Q | |||
</math>. | |||
'''Proof:''' If the points coincide, <math>\,P = Q</math>, we just saw that the difference vector is the zero vector. Conversely, assume that <math>\,P \ne Q</math> and <font style = "vertical-align: 10%"><math>\overrightarrow{PQ} = \vec{0}</math></font>. Then for an arbitrary point <font style = "vertical-align: 8%"><math>\,R</math></font>, | |||
:<math> | :<math> | ||
\overrightarrow{PQ} | \vec{0} = \overrightarrow{PQ} = -\overrightarrow{RP} + \overrightarrow{RQ} \quad\Longrightarrow\quad | ||
\overrightarrow{ | \overrightarrow{RP} = \overrightarrow{RQ}, | ||
</math> | </math> | ||
which implies that the same vector in ''V'' connects <font style = "vertical-align: 10%"><math>\,R </math></font> in ''A'' with two different points, which by postulate 2 is forbidden. | |||
==Parallelogram law== | ==Parallelogram law== | ||
[[Image:Affine points.png|right|thumb|200px|Parallelogram law]] | [[Image:Affine points.png|right|thumb|200px|Parallelogram law]] | ||
Revision as of 09:13, 7 November 2008
The 2- and 3-dimensional point spaces studied in elementary Euclidean geometry are examples of affine spaces, A2 and A3, respectively.
Assume that any two points P and Q in a space A can be connected by a line segment in A; this possibility is Axiom 1 of Euclidean geometry. If we order P and Q (we say that P comes before Q), then the line segment obtains a direction (points from P to Q) and has become a vector, the difference vector . When all difference vectors can be mapped onto vectors of the same n-dimensional vector space Vn, we may call the point space A an affine space of dimension n, written An.
Usually one takes as a difference space an inner product space. Its elements have a well-defined length, namely, the square root of the inner product of the vector with itself. The distance between points P and Q in an affine space is then defined as the length of the image of in Vn. Difference vectors that are mapped onto the same element of Vn are said to be parallel, they differ from each other by translation.
Formal definition
We will restrict the definition to vector spaces over the field of real numbers.
Let V be an n-dimensional vector space and A a set of elements that we will call points. Assume that a relation between points and vectors is defined in the following way:
- To every ordered pair P, Q of A there is assigned a vector of V, called the difference vector, denoted by .
- To every point P of A and every vector of V there exists exactly one point Q in A, such that .
- If P, Q, and R are three arbitrary points in A, then
If these three postulates hold, the set A is called an n-dimensional affine space with difference space V.
Immediate consequences:
Lemma:
- .
Proof: If the points coincide, , we just saw that the difference vector is the zero vector. Conversely, assume that and . Then for an arbitrary point ,
which implies that the same vector in V connects in A with two different points, which by postulate 2 is forbidden.
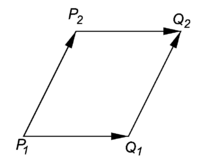
Parallelogram law
Consider four points in A: P1, P2, Q1, and Q2. Assume that the following difference vectors are equal, i.e., the corresponding line-segments in A are parallel and of equal length:
then the four points form a parallelogram, that is,
see the figure.
Proof Subtract the following equations:
This gives
Position vector
Choose a fixed point O in the affine space A. Every point P is uniquely determined by the vector (by the second requirement). The vector is the position vector of P with respect to O. After choosing O every point P can be uniquely identified with its corresponding position vector in V. Choice of another point O′ gives a translation of by , for
with , the position vector of P with respect to O′.