Gravitational lens

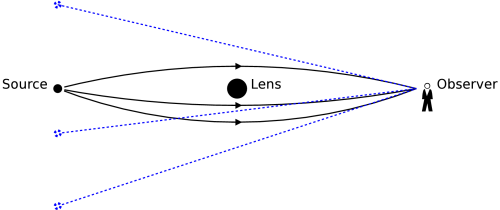
In a gravitational lensing scenario, light traveling from a distant astronomical source (e.g. a galaxy) to an observer is deflected by the gravitational field of an intermediate object (e.g. a cluster of galaxies), therefore designated the gravitational lens. Because of this, the observer will see the source in a direction different from the one in which the source would be observed if the gravitational lens were absent. Furthermore, it is possible for light rays to reach the observer by multiple paths, causing multiple images of the same source to appear.

History

In Newtonian mechanics, the path of a test particle in a gravitational field does not depend on the mass of the test particle. For this reason, one can argue that even in the absolute space and time of Newton, light does not always go in a straight line, but can be deflected noticeably by objects with a sufficiently strong gravitational field. In 1804, J. von Soldner was the first one to publish the Newtonian value of the deflection angle:

${\hat {\alpha }}_{Newtonian}={\frac {2GM}{c^{2}d}}$

In this equation, G is the gravitational constant, M the mass of the object deflecting the light, c is the speed of light and d is the impact parameter of the light ray.

More than a century later, after having completed his general theory of relativity, Albert Einstein published a new expression, differing only by a factor of two from the Newtonian result:

${\hat {\alpha }}={\frac {4GM}{c^{2}d}}$

For a light ray passing close to the sun, the value of this angle is 1.74 arcsec. During a solar eclipse, the bending angle can be calculated by comparing the positions of stars close to the sun to the positions where one would expect these stars to be seen if their light rays were not deflected by the sun. In 1919, a team of astronomers led by Eddington set out to measure the deflection angle during a total eclipse and reported an agreement with Einstein's predicted value with 20% uncertainty. Later measurements drastically reduced this amount of uncertainty to a value of 0.02%.

After this, gravitational deflection of light received only little attention for a very long time. Around 1964 Liebes and especially Refsdal revived the gravitational lens effect briefly, but it wasn't until the first actual gravitationally lensed quasar QSO 0957+561 was observed in 1979 that the subject gained much interest. Since then, a huge amount of articles about gravitational lensing have been published.

Regimes

Gravitational lens phenomena are usually subdivided into three categories: strong lensing, weak lensing and microlensing. In the strong lensing regime, the gravitational lens effect causes multiple images of the same source to be observed. Often, there are severely distorted images such as giant arcs. For strong lensing to occur, the source, the gravitational lens and the observer have to be sufficiently aligned and the bending angle has to be large enough to allow the different images to be resolved.

In some cases the alignment is not good enough to produce multiple images, but the effect of the gravitational lens can still be seen through the presence of a multitude of slightly distorted images. This is normally referred to as weak lensing. Since it is impossible to know the exact shape of a source a priori, a statistical analysis of a large number of images is necessary to acquire information about the distortions caused by the gravitational lens.

Finally, it is possible that the gravitational lens does cause multiple images, but that these simply cannot be resolved by our telescopes. However, since a gravitational lens can cause images to become brighter, the presence of a gravitational lens can be detected when source and lens move with respect to each other. In this case, the gravitational lens effect is referred to as microlensing.

The thin lens approximation

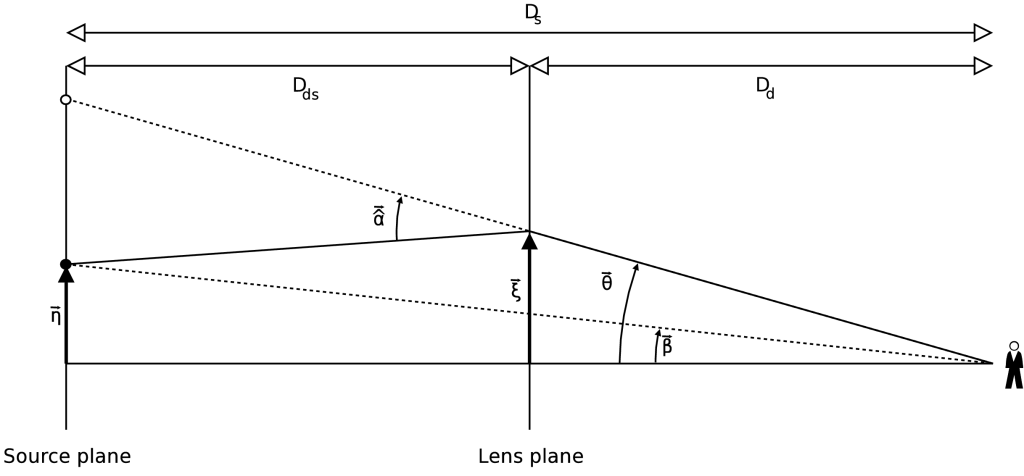
To describe gravitational lensing systems usually one works in the weak-field limit, for which the bending angle is well approximated by the formula above. Then, as a further approximation, one assumes that light travels in a straight line from source to lens where it is deflected instantaneously. Afterwards, the light continues along a straight line again. The three dimensional mass distribution of the gravitational lens is replaced by a two dimensional one, lying in the so-called lens plane. The figure below illustrates this situation.

If $\rho$ describes the three dimensional mass distribution of the gravitational lens, the two dimensional mass distribution $\Sigma$ is obtained as follows:

$\Sigma ({\vec {\xi }})=\int \rho (\xi _{1},\xi _{2},z)\mathrm {d} z$,

assuming the z-axis is directed from observer to lens.

Using Einstein's expression for the deflection of a light ray by a pointmass, the deflection angle for an arbitrary mass distribution can be written as:

${\hat {\vec {\alpha }}}({\vec {\xi }})={\frac {4G}{c^{2}}}\int \Sigma ({\vec {\xi '}}){\frac {{\vec {\xi }}-{\vec {\xi '}}}{|{\vec {\xi }}-{\vec {\xi '}}|^{2}}}\mathrm {d} ^{2}\xi '$.

Since all the angles involved are small, the following relation holds for a light ray connecting source and observer:

${\vec {\eta }}+D_{ds}{\hat {\vec {\alpha }}}={\frac {D_{s}}{D_{d}}}{\vec {\xi }}$,

from which the lens equation (or ray-trace equation) follows immediately:

${\vec {\beta }}({\vec {\theta }})={\vec {\theta }}-{\frac {D_{ds}}{D_{s}}}{\hat {\vec {\alpha }}}({\vec {\theta }})$.

The lens equation relates the viewing directions ${\vec {\theta }}$ and ${\vec {\beta }}$. If you look in a direction ${\vec {\theta }}$, you see what you would see in direction ${\vec {\beta }}$ if the gravitational lens were not present. Note that the distances $D_{d}$, $D_{s}$ and $D_{ds}$ are actually angular diameter distances, so that in general, $D_{s}\neq D_{d}+D_{ds}$.

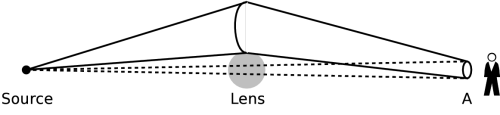
It's easy to see that a gravitational lens can also influence the flux received from a source. In the example at the right, a source emits photons isotropically. In absence of the gravitational lens, the observer using a detector of area A, detects the photons emitted by the source in a relatively small solid angle (marked by dotted lines). However, due to the deflection of light rays by the lens, the detector receives the photons emitted in a much larger solid angle. In this case, the detector will measure a much larger flux, corresponding to a brighter image. In the same way it is possible that an image becomes much dimmer.

This so-called magnification factor $\mu$ can be calculated using the lens equation as follows:

$\mu ^{-1}=\mathrm {det} \left({\frac {\partial \beta _{i}}{\partial \theta _{j}}}\right)$.

Applications

Cosmic telescope

As is mentioned above, a gravitational lens can have a serious effect on how the observer perceives an astronomical object. It is possible that one of the images (or several images) are stretched severely, and precisely these images will also become brighter. Because of this, a gravitational lens can make very distant objects visible, which would otherwise be far to dim to observe. For this reason, gravitational lenses are sometimes referred to as cosmic telescopes.

Abell 2218 is a cluster of galaxies acting as a gravitational lens for several background objects. Thanks to its magnifying effect, an extremely distant galaxy has been observed.

Detection of planets

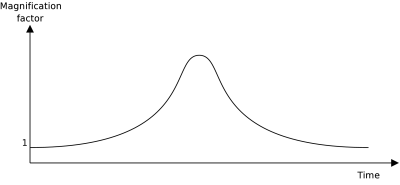
When an object moves with respect to another star acting as a gravitational lens, this will produce a typical brightness curve such as the one on the right. If a planet orbits the star acting as a gravitational lens, it is possible that the measured brightness curve reveals the presence of this planet by introducing an additional bump for example. The advantage of this planet detection method is that it permits the discovery of planets having masses of only a small fraction of the star's mass. A handful of planets has already been detected this way.

Lens inversion

[1]