Black-body radiation
Planck's blackbody equation describes the spectral exitance of an ideal blackbody.
![{\displaystyle M(\lambda ,T)[{\frac {W}{m^{2}m}}]={\frac {2\pi hc^{2}}{\lambda ^{5}(\exp ^{\frac {hc}{\lambda KT}}-1)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1eba9291ddfe915f2a665dac12ec9153fc8738d6)
where:
| Symbol | Units | Description |
|---|---|---|
| Input wavelength | ||
| Input temperature | ||
| Planck's constant | ||
| Speed of light in vacuum | ||
| Boltzmann constant |
![{\displaystyle [m]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b649f5418f2ac84d66063f41319368b0926ccec4)
![{\displaystyle [K]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b6c25071903364b1b51e69ffa99ec95f6d122d5)
![{\displaystyle [J*s]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/751c5bea56bc672d42ac27457e7e940b269e8990)
![{\displaystyle [{\frac {m}{sec}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c5921e89e1b41df1b07950bebb522fb96c81fd8)
![{\displaystyle [erg*K]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d64f4a0cf071f92fcf1ee72a31a5f47e39d8b51)
Note that the input is in meters and that the output is a spectral irradiance in . Omitting the term from the numerator gives the blackbody emission in terms of radiance, with units where "sr" is steradians. There is a different formulation of the Planck equation in terms of frequency.
![{\displaystyle [W/m^{2}*m]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c244377e247036110f6b9089c4a81bac21dbf54)
![{\displaystyle [W/m^{2}*sr*m]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f0037b79d48b97852db90d92db992888f9cf7a9)
Taking the first derivative leads to the wavelength with maximum exitance. This is known as the Wien Displacement Law.
A closed form solution exists for the integral of the Planck blackbody equation over the entire spectrum. This is the Stefan-Boltzmann equation. In general, there is no known closed-form solution for the definite integral of the Planck blackbody equation; numerical integration techniques must be used.
The relationship between the ideal blackbody exitance and the actual exitance of a surface is given by emissivity.
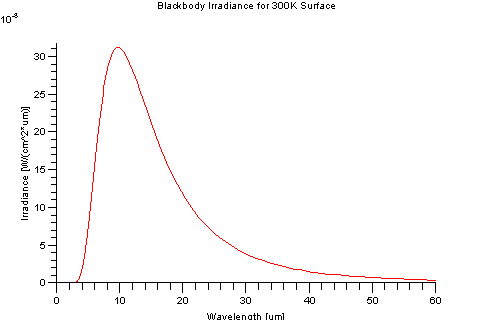
An ideal blackbody at 300K (~30 Celsius) has a peak emission 9.66 microns. It has virtually no self-emission before 2.5 microns, hence self-emission is typically associated with the "thermal" regions of the EM spectrum. However, the Sun has a peak emission around 0.49 microns which is in the visible region of spectrum.