Black-body radiation
A black body absorbs and then re-emits all incident EM radiation. By definition it has an absorptivity and emissivity of 1, and a transmissivity and reflectivity of 0. The Planck black body equation describes the spectral exitance of an ideal black body. The study of black-body radiation was an integral step in the formulation of quantum mechanics.
Planck's Law: Wavelength
Formulated in terms of wavelength:
where:
| Symbol | Units | Description |
|---|---|---|
| Input wavelength | ||
| Input temperature | ||
| Planck's constant | ||
| Speed of light in vacuum | ||
| Boltzmann constant |
Note that the input is in meters and that the output is a spectral irradiance in . Omitting the term from the numerator gives the blackbody emission in terms of radiance, with units where "sr" is steradians.
Planck's Law: Frequency
Formulated in terms of frequency:
where:
| Symbol | Units | Description |
|---|---|---|
| Input frequency |
All other units are the same as for the Wavelength formulation. Again, dropping the from the numerator gives the result in radiance rather than irradiance.
Properties of the Planck Equation
Taking the first derivative of the Planck's law wavelength equation leads to the wavelength with maximum exitance as a function of temperature. This is known as Wien's displacement law:
A closed-form solution exists for the integral of the Planck blackbody equation over the entire spectrum. This is the Stefan-Boltzmann equation. In general, there is no closed-form solution for the definite integral of the Planck blackbody equation; numerical integration techniques must be used.[1][2]
The ratio of the actual exitance of a surface to that of an ideal blackbody is the surface's emissivity, which is always less than or equal to 1.
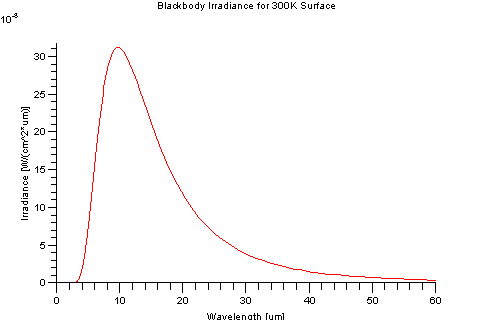
An ideal blackbody at 300K (27 Celsius) has a peak emission at 9.66 microns. It has virtually no self-emission below 2.5 microns, hence self-emission is typically associated with the "thermal" regions of the EM spectrum. However, the Sun can be characterized as a 5900K blackbody and has a peak emission at around 0.49 microns, which is in the visible region of the electromagnetic spectrum.
The Planck equation has a single maximum. The wavelength with peak exitance becomes shorter as temperature increases. The total exitance increases with temperature.
Citations
- ↑ Paez, G. and Strojnik, M. "Integrable and differentiable approximations to the generalized Planck's equations." Proceedings of SPIE. Vol 3701, pp 95-105. DOI=10.1117/12.352985
- ↑ Lawson, Duncan. "A closer look at Planck's blackbody equation." Physics Education 32.5 (Sept. 1997): 321-326. IOP. 19 Sept. 2007 <http://stacks.iop.org/0031-9120/32/321>.
![{\displaystyle M(\lambda ,T)[{\frac {W}{m^{2}m}}]={\frac {2\pi hc^{2}}{\lambda ^{5}(\exp ^{\frac {hc}{\lambda kT}}-1)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ab4d39f89f3600b5405866eb30bd16a2795bf1c)

![{\displaystyle [m]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b649f5418f2ac84d66063f41319368b0926ccec4)

![{\displaystyle [K]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b6c25071903364b1b51e69ffa99ec95f6d122d5)

![{\displaystyle [J*s]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/751c5bea56bc672d42ac27457e7e940b269e8990)

![{\displaystyle [{\frac {m}{sec}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c5921e89e1b41df1b07950bebb522fb96c81fd8)

![{\displaystyle [erg*K]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d64f4a0cf071f92fcf1ee72a31a5f47e39d8b51)
![{\displaystyle [W/m^{2}*m]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c244377e247036110f6b9089c4a81bac21dbf54)

![{\displaystyle [W/m^{2}*sr*m]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f0037b79d48b97852db90d92db992888f9cf7a9)
![{\displaystyle M(v,T)[{\frac {W}{m^{2}Hz}}]={\frac {2\pi hv^{3}}{c^{2}(\exp ^{\frac {hv}{kT}}-1)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d91e62cc64b0ae30ad3b1ede2d020489268df7ac)

![{\displaystyle [Hz]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33dac5031f1f01184208e90edb8d25bf37e2f399)