Affine space

The 2-dimensional plane, well-known from elementary Euclidean geometry, is an example of an affine space. Remember that in elementary geometry none of the points in the plane is special—there is no origin. A real n-dimensional affine space is distinguished from the vector space Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}^n} by having no special point, no fixed origin.

From elementary geometry we know that any two points in a plane (a collection of infinitely many points) can be connected by a line segment. If the points P and Q in a plane are ordered with P before Q, the line segment connecting the two becomes an arrow pointing from P to Q. This arrow can be mapped onto a vector, the difference vector, denoted by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overrightarrow{PQ}} . If all arrows in a plane can be mapped onto vectors of a 2-dimensional vector space V₂, called the difference space, the plane is an affine space of dimension 2, denoted by A₂. Arrows that are mapped onto the same vector in the difference space are said to be parallel, they differ from each other by translation.

In elementary analytic geometry, the map of arrows onto vectors is almost always defined by the choice of an origin O, which is a point somewhere in the plane. Clearly, an arbitrary point P is the head of an arrow with tail in the origin and corresponding with the unique difference vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overrightarrow{OP}} . All arrows with tail in O are mapped one-to-one onto a 2-dimensional difference space V₂, with the vector addition in V₂ in one-to-one correspondence with the parallelogram rule for the addition of arrows in the plane.

Usually one equips the difference space with an inner product, turning it into an inner product space. Its elements have well-defined length, namely, the square root of the inner product of the vector with itself. The distance between any two points P and Q may now be defined as the length of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overrightarrow{PQ}} in V₂. A two-dimensional affine space, with this distance defined between the points, is the Euclidean plane known from high-school geometry.

Upon formalizing and generalizing the definition of an affine space, we replace the dimension 2 by an arbitrary finite dimension n and replace arrows by ordered pairs of points ("head" and "tail") in a given point space A. Briefly, A is an affine space of dimension n if there exists a map of the Cartesian product, A × A onto a vector space of dimension n. This map must satisfy certain axioms that are treated in the next section. If the dimension needs to be exhibited, we may write A_n for the affine space of dimension n.

Formal definition

We will restrict the definition to vector spaces over the field Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}} of real numbers.

Let V be an n-dimensional vector space and A a set of elements that we will call points. Assume that a relation between points and vectors is defined in the following way:

1. To every ordered pair P, Q of A there is assigned a vector of V, called the difference vector, denoted by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overrightarrow{PQ} \in V} .
2. To every point P of A and every vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{v}} of V there exists exactly one point Q in A, such that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overrightarrow{PQ} = \vec{v}} .
3. If P, Q, and R are three arbitrary points in A, then

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overrightarrow{PQ} + \overrightarrow{QR} = \overrightarrow{PR}. }

If these three postulates hold, the set A is an n-dimensional affine space with difference space V.

Two immediate and important consequences are:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \overrightarrow{PP} + \overrightarrow{PR} &= \overrightarrow{PR} &\Longrightarrow\quad \overrightarrow{PP} = \vec{0}.\qquad \\ \overrightarrow{PQ} + \overrightarrow{QP} &= \vec{0}\qquad &\Longrightarrow\quad \overrightarrow{PQ} = -\overrightarrow{QP}. \\ \end{align} }

Lemma 1:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overrightarrow{PQ} = \vec{0} \quad \Longleftrightarrow\quad P = Q } .

Proof:   If the points coincide, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,P = Q} , we just saw that the difference vector is the zero vector. Conversely, assume that   Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,P \ne Q}   and   Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overrightarrow{PQ} = \vec{0}} . Then for an arbitrary point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,R} ,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{0} = \overrightarrow{PQ} = -\overrightarrow{RP} + \overrightarrow{RQ} \quad\Longrightarrow\quad \overrightarrow{RP} = \overrightarrow{RQ}, }

which implies that the same vector in V connects Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,R } in A with two different points, which by postulate 2 is forbidden.

Parallelogram law

CC Image
The parallelogram law in the 2-dimensional Euclidean plane.

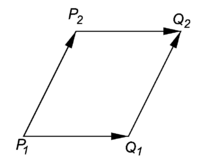
Consider four points in A:   P₁, P₂, Q₁, and Q₂. Assume that the following difference vectors are equal,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overrightarrow{P_1Q_1} = \overrightarrow{P_2Q_2} }

then we may exchange Q₁ and P₂,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overrightarrow{P_1P_2} = \overrightarrow{Q_1Q_2}. }

See the figure for a concrete example in which the four points form a parallelogram.

Proof:   Subtract the following equations:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \overrightarrow{P_1P_2} &= \overrightarrow{P_1Q_2} - \overrightarrow{P_2Q_2}\\ \overrightarrow{Q_1Q_2} &= \overrightarrow{P_1Q_2} - \overrightarrow{P_1Q_1}.\\ \end{align} }

This gives

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overrightarrow{P_1P_2} - \overrightarrow{Q_1Q_2} = - \overrightarrow{P_2Q_2} + \overrightarrow{P_1Q_1} = \vec{0}. }

Position vector

Choose a fixed point O in the affine space A, an origin. Every point P is uniquely determined by the vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overrightarrow{OP} \in V} . Indeed, suppose that there is another point Q such that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overrightarrow{OP} = \overrightarrow{OQ} } , it then follows from lemma 1 that P = Q.

The vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{v}\equiv\overrightarrow{OP}} is the position vector of P with respect to O. After choosing O every point P in A is uniquely identified by its corresponding position vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{v} \in V} .

Choice of another origin O ′ gives a translation of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{v}} by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\vec{t} \equiv -\overrightarrow{OO\;'}} , for

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{v} \equiv \overrightarrow{OP} = \overrightarrow{OO\;'}+ \overrightarrow{O'P} = \vec{t} + \vec{v}\;' \quad\Longrightarrow\quad \vec{v}\;' = \vec{v} - \vec{t} }

with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{v}\;' } the position vector of P with respect to O ′.

Affine coordinate systems

An affine coordinate system

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{B} \equiv (O; \,\vec{e}_1, \vec{e}_2,\ldots, \vec{e}_n) }

consists of an origin O in A and a basis   Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{e}_i\,\, (i=1,\ldots,n)}   of the difference space V. Then every point P in A determines a system of n real numbers x_i (i = 1, ..., n) by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overrightarrow{OP} = \sum_{i=1}^n \, x_i\, \vec{e}_i \in V. }

The numbers x_i (i = 1, ..., n) are the affine coordinates of P with respect to the given coordinate system. Note that O has the coordinates x_i = 0.

Consider now two different affine coordinate systems,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{B} \equiv (O; \,\vec{e}_1, \vec{e}_2,\ldots, \vec{e}_n)\quad \hbox{and}\quad\mathbb{B}' \equiv (O'; \,\vec{f}_1, \vec{f}_2,\ldots, \vec{f}_n). }

Write

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{f}_i = \sum_{j=1}^n \vec{e}_j \, A_{ji} \quad\hbox{and}\quad \overrightarrow{OO'} = \sum_{i=1}^n t_i\, \vec{e}_i. }

The matrix (A_{i j}) transforms the one basis of V into the other, hence it is a square regular (invertible) matrix. The real numbers t_i are the affine coordinates of O′ relative to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{B}} .

Express a fixed point P with respect to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{B}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{B}'} ,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overrightarrow{OP} = \sum_{i=1}^n \, x_i\, \vec{e}_i\quad\hbox{and}\quad \overrightarrow{O'P} = \sum_{i=1}^n \, y_i\, \vec{f}_i }

Insert into the second equation

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overrightarrow{O'P} = \overrightarrow{OP} -\overrightarrow{OO'} }

and express Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{f}_i} in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{e}_j} , then

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sum_{i=1}^n y_i\, \vec{f}_i = \sum_{j=1}^n (x_j - t_j) \vec{e}_j= \sum_{j=1}^n \vec{e}_j \sum_{j=1}^n \, A_{ji}\, y_i, }

so that the transformation from the one affine coordinate system to the other is,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (x_j-t_j) = \sum_{i=1}^n A_{ji}\, y_i \quad \Longrightarrow\quad \mathbf{x} = \mathbf{t} + \mathbf{A} \mathbf{y}, }

where we introduced bold lowercase letters for real column-vectors (stacks of n real numbers) and the boldface capital indicates an n × n matrix. Inversion of the non-singular (regular) matrix (A_{i j}) gives the inverse transformation,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_j = \sum_{i=1}^n (A^{-1})_{ji}\, (x_i-t_i) \quad \Longrightarrow\quad \mathbf{y} = \mathbf{A}^{-1} \,(\mathbf{x} - \mathbf{t}). }

Affine maps

Let P → P′ be a mapping of the affine space A into itself; if the map satisfies the following two conditions, it is an affine map.

(i) Conserve "parallelism". (In the Euclidean plane this condition implies that sets of mutually parallel arrows are mapped onto sets of mutually parallel arrows. Note, however, that in general the mapped arrows are not parallel to the original arrows):

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overrightarrow{P_1 Q_1} = \overrightarrow{P_2 Q_2}\quad \Longrightarrow\quad \overrightarrow{P'_1 Q'_1} = \overrightarrow{P'_2 Q'_2} }

(ii) The map is linear in the difference space. That is, the map φ: V → V defined by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varphi(\overrightarrow{P_1 Q_1}) = \overrightarrow{P'_1 Q'_1} \qquad\qquad\qquad\qquad(1) }

is linear. A translation is an affine map with φ the identity operation,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \varphi(\overrightarrow{P_1 Q_1})\equiv \overrightarrow{P'_1 Q'_1} = \overrightarrow{P_1 Q_1}. }

Here the origin and the image are parallel.

CC Image
Fig. 1. Affine map. Here φ is linear, but not necessarily length preserving.

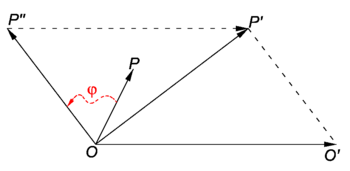
Given two points O and O′ and a linear map φ: V → V. There exists exactly one affine map that sends O into O′ and induces φ on V. This is the map

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overrightarrow{OP\,'} = \overrightarrow{OO\,'} + \varphi(\overrightarrow{OP}) , }

because (see Fig. 1),

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} \varphi(\overrightarrow{OP}) &= \overrightarrow{OP\,''}\\ \overrightarrow{P''P\,'} &= \overrightarrow{OO\,'}\\ \overrightarrow{OP\,'} &= \overrightarrow{P''P\,'} + \overrightarrow{OP\,''} = \overrightarrow{OO\,'} + \varphi(\overrightarrow{OP}) . \end{align} }

Note: since Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overrightarrow{OP\,''} = \overrightarrow{O'P\,'}} by the parallelogram law (see above), the map φ may also be defined as

$\varphi ({\overrightarrow {OP}})={\overrightarrow {O'P\,'}},$

as was done in Eq. (1).

Choose a basis

$(O;\,{\vec {e}}_{1},{\vec {e}}_{2},\ldots ,{\vec {e}}_{n})$

then

${\overrightarrow {OP\,'}}=\sum _{i=1}^{n}p'_{i}{\vec {e}}_{i},\qquad {\overrightarrow {OO\,'}}=\sum _{i=1}^{n}t_{i}{\vec {e}}_{i},\qquad \varphi ({\overrightarrow {OP}})=\sum _{i=1}^{n}{\vec {e}}_{i}\sum _{j=1}^{n}F_{ij}p_{j},$

from which follows the matrix-vector expression for an affine map,

$p'_{i}=t_{i}+\sum _{j=1}^{n}F_{ij}p_{j},\quad i=1,\ldots ,n\quad \Longleftrightarrow \quad \mathbf {p} '=\mathbf {t} +\mathbf {F} \mathbf {p}$

Often one writes the last expression for an affine map with the aid of a square (n+1) × (n+1) matrix that contains F on the diagonal and that is augmented with the translation vector t and the number 1,

${\begin{pmatrix}\mathbf {p} '\\1\end{pmatrix}}={\begin{pmatrix}\mathbf {F} &\mathbf {t} \\\mathbf {0} &1\\\end{pmatrix}}{\begin{pmatrix}\mathbf {p} \\1\end{pmatrix}}.$

Euclidean space

Let A be an affine space with difference space V on which a positive-definite inner product is defined. Then A is called a Euclidean space. The distance between two point P and Q is defined by the length ,

$\rho (P,Q)=|{\overrightarrow {PQ}}|\equiv \left({\overrightarrow {PQ}},\;{\overrightarrow {PQ}}\right)^{1/2}$

where the expression between round brackets indicates the inner product of the vector with itself. It follows from the properties of the real inner product that the distance has the usual properties,

1. ρ(P,Q) ≥ 0 and ρ(P,Q) = 0 if and only if P = Q
2. ρ(P,Q) = ρ(Q,P)
3. ρ(P,Q) ≤ ρ(P,R) + ρ(R,Q)

A rigid motion of a Euclidean space is an affine map which preserves distances. The linear map φ on V is then a rotation. Conversely, given a rotation φ and two points P and P′ then there exists exactly one rigid motion which sends P into P′ and induces φ on V.

Notes and references

• A. Lichnerowicz, Elements of Tensor Calculus, Translated from the French by J. W. Leech and D. J. Newman, Methuen (London) 1962.
• W. H. Greub, Linear Algebra, 2nd edition, Springer (Berlin) 1963.