Talk:Gravitational lens: Difference between revisions
imported>Jori Liesenborgs No edit summary |
imported>Jori Liesenborgs (Added backup of old 'thin lens approximation section') |
||
| Line 21: | Line 21: | ||
: Thanks for your feedback Fredrik. You're definitely right: the "only" gives the wrong impression. The history section also needs some more work (and references), currently it only contains the facts I could remember. The "thin lens approximation" section is going to be replaced by a "lensing formalism" section, which will also describe the time delay function, lensing potential etc. Anyway, I'm glad I'm not the only one reading the page :) | : Thanks for your feedback Fredrik. You're definitely right: the "only" gives the wrong impression. The history section also needs some more work (and references), currently it only contains the facts I could remember. The "thin lens approximation" section is going to be replaced by a "lensing formalism" section, which will also describe the time delay function, lensing potential etc. Anyway, I'm glad I'm not the only one reading the page :) | ||
: [[User:Jori Liesenborgs|Jori Liesenborgs]] | [[User talk:Jori Liesenborgs|Talk]] 15:40, 9 March 2007 (CST) | : [[User:Jori Liesenborgs|Jori Liesenborgs]] | [[User talk:Jori Liesenborgs|Talk]] 15:40, 9 March 2007 (CST) | ||
== Backup of old 'thin lens approximation' section == | |||
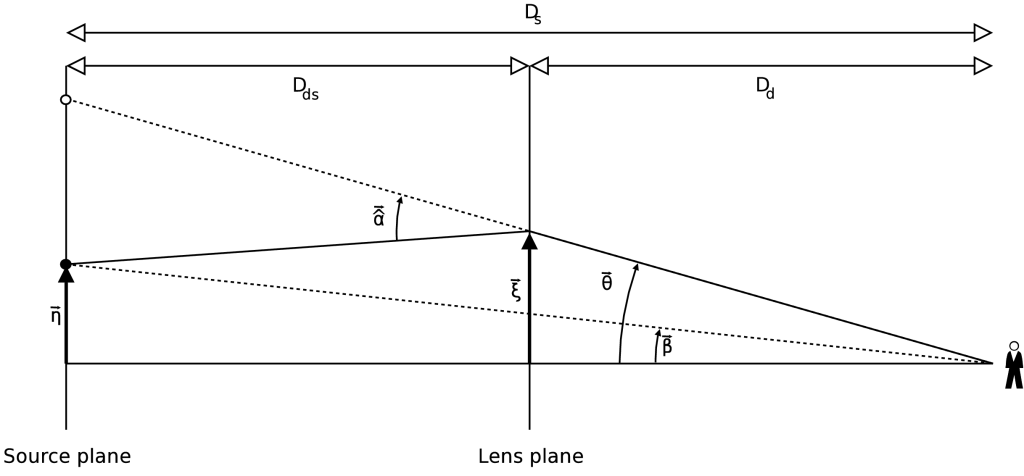
To describe gravitational lensing systems usually one works in the so-called weak-field limit, for which the bending | |||
angle is well approximated by the formula above. Then, as a further approximation, one assumes that light | |||
travels in a straight line from source to lens where it is deflected instantaneously. Afterwards, the | |||
light continues along a straight line again. The three dimensional mass distribution of the gravitational | |||
lens is replaced by a two dimensional one, lying in the so-called lens plane. The figure below illustrates | |||
this situation. | |||
[[Image:GravitationalLensEquation.png]] | |||
If <math>\rho</math> describes the three dimensional mass distribution of the gravitational lens, the | |||
two dimensional mass distribution <math>\Sigma</math> is obtained as follows: | |||
<math>\Sigma(\vec{\xi}) = \int \rho(\xi_1,\xi_2,z) \mathrm{d}z</math>, | |||
assuming the ''z''-axis is directed from observer to lens. | |||
Using Einstein's expression for the deflection of a light ray by a pointmass, the deflection angle for | |||
an arbitrary mass distribution can be written as: | |||
<math>\hat{\vec{\alpha}}(\vec{\xi}) = \frac{4 G}{c^2} \int \Sigma(\vec{\xi'}) \frac{\vec{\xi}-\vec{\xi'}}{|\vec{\xi}-\vec{\xi'}|^2} \mathrm{d}^2\xi'</math>. | |||
Since all the angles involved are small, the following relation holds for a light ray connecting source | |||
and observer: | |||
<math>\vec{\eta} + D_{ds}\hat{\vec{\alpha}} = \frac{D_s}{D_d}\vec{\xi}</math>, | |||
from which the ''lens equation'' (or ray-trace equation) follows immediately: | |||
<math>\vec{\beta}(\vec{\theta}) = \vec{\theta} - \frac{D_{ds}}{D_s}\hat{\vec{\alpha}}(\vec{\theta})</math>. | |||
The lens equation relates the viewing directions <math>\vec{\theta}</math> and <math>\vec{\beta}</math>. | |||
If you look in a direction <math>\vec{\theta}</math>, you see what you ''would'' see in direction | |||
<math>\vec{\beta}</math> ''if'' the gravitational lens were not present. | |||
Note that the distances <math>D_d</math>, <math>D_s</math> and <math>D_{ds}</math> are actually | |||
[[angular diameter distance]]s, so that in general, <math>D_s \neq D_d + D_{ds}</math>. | |||
{| align=right | |||
|- | |||
| | |||
[[Image:GravitationalLensMagnification.png|The effect of a gravitational lens on the flux received from a source]] | |||
|} | |||
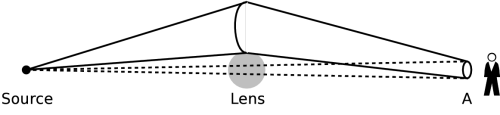
It's easy to see that a gravitational lens can also influence the [[flux]] received from a source. | |||
In the example at the right, a source emits [[photon]]s [[isotropy|isotropically]]. In absence of the gravitational | |||
lens, the observer using a detector of area ''A'', detects the photons emitted by the source in | |||
a relatively small [[solid angle]] (marked by dotted lines). However, due to the deflection of light | |||
rays by the lens, the detector receives the photons emitted in a much larger solid angle. In this | |||
case, the detector will measure a much larger flux, corresponding to a brighter image. In the same | |||
way it is possible that an image becomes much dimmer. | |||
This so-called magnification factor <math>\mu</math> can be calculated using the lens equation as follows: | |||
<math>\mu^{-1} = \mathrm{det}\left(\frac{\partial \beta_i}{\partial \theta_j}\right)</math>. | |||
Revision as of 12:10, 10 March 2007
Initial version
Just finished an initial version (with home-made images :-) ) which should contain most of the basic information. Feel free to comment... --Jori 15:26, 26 February 2007 (CST)
A few thoughts:
- Albert Einstein published a new expression, differing only by a factor of two from the Newtonian result
I wouldn't call a factor of two an "only". The difference is enormous compared to, say, the Lorentz factor for objects moving at classical speeds. In fact, isn't the huge difference the point of the section? Had the factor been, say, 1.01, Einstein's theory would not have been verified (at that time). Are there actually instances in which the Newtonian value is useful? The article could be a bit more explicit about whether the Eddington measurement did or did not render the classical approximation useless. With the "only" in there, I get the impression that it didn't.
- d is the impact parameter of the light ray
I have no idea what an impact parameter is. A short definition wouldn't hurt.
Also, in the "thin lens approximation" section, there are a few undefined variables. The text should be comprehensible without looking at the image.
Instead of "Note that the distances are", I'd write "The distances are", since I don't see how one could note this (without prior knowledge) from the information given in the preceding text.
Fredrik Johansson 15:37, 8 March 2007 (CST)
- Thanks for your feedback Fredrik. You're definitely right: the "only" gives the wrong impression. The history section also needs some more work (and references), currently it only contains the facts I could remember. The "thin lens approximation" section is going to be replaced by a "lensing formalism" section, which will also describe the time delay function, lensing potential etc. Anyway, I'm glad I'm not the only one reading the page :)
- Jori Liesenborgs | Talk 15:40, 9 March 2007 (CST)
Backup of old 'thin lens approximation' section
To describe gravitational lensing systems usually one works in the so-called weak-field limit, for which the bending angle is well approximated by the formula above. Then, as a further approximation, one assumes that light travels in a straight line from source to lens where it is deflected instantaneously. Afterwards, the light continues along a straight line again. The three dimensional mass distribution of the gravitational lens is replaced by a two dimensional one, lying in the so-called lens plane. The figure below illustrates this situation.
If describes the three dimensional mass distribution of the gravitational lens, the two dimensional mass distribution is obtained as follows:
,
assuming the z-axis is directed from observer to lens.
Using Einstein's expression for the deflection of a light ray by a pointmass, the deflection angle for an arbitrary mass distribution can be written as:
.
Since all the angles involved are small, the following relation holds for a light ray connecting source and observer:
,
from which the lens equation (or ray-trace equation) follows immediately:
.
The lens equation relates the viewing directions and . If you look in a direction , you see what you would see in direction if the gravitational lens were not present. Note that the distances , and are actually angular diameter distances, so that in general, .
It's easy to see that a gravitational lens can also influence the flux received from a source. In the example at the right, a source emits photons isotropically. In absence of the gravitational lens, the observer using a detector of area A, detects the photons emitted by the source in a relatively small solid angle (marked by dotted lines). However, due to the deflection of light rays by the lens, the detector receives the photons emitted in a much larger solid angle. In this case, the detector will measure a much larger flux, corresponding to a brighter image. In the same way it is possible that an image becomes much dimmer.
This so-called magnification factor can be calculated using the lens equation as follows:
.