Artificial neuron

Artificial neurons are processing units based on the biological neural model. The first artificial neuron model was created by McCullough and Pitts, and then newer and more complex models have appeared. Since the connectivity in the biological neurons is higher, artificial neurons must be considered as only an approximation to the biological model.

Artifical neurons can be organized and connected in order to create artificial neural networks, which process the data carried through the neural connections in different layers. Learning algorithms can also be applied to artificial neural networks in order to modify their behavior.

McCullough-Pitts neuron with 4 inputs.

Behavior

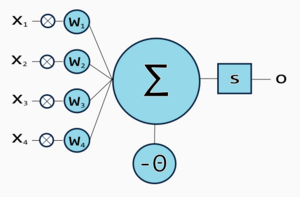
A neuron may have multiple inputs, each input has an assigned value called weight, which represents the strength of the connection between the source and destination neuron. The input signal value is multiplied by the weight $w\in \left[0\dots 1\right]$.

The sum of all input values multiplied by their respective weights is called activation, or weighted-sum.

$a=\sum _{i=0}^{n}w_{i}x_{i}$

After the activation is produced, a function modifies it, producing an output. That function is often called transfer function and its purpose is to filter the activation. The output value $y$ can be expressed as:

$y=\varphi \left(\sum _{i=0}^{n}w_{i}x_{i}\right)$

Transfer Functions

Transfer function is the name given for the functions which filter the activation value. This functions can be discrete or continuous.

Step function

The step function (also called hard-limiter) is piecewise defined function used to produce binary outputs. In this function, the result is 0 if the activation is less than a value called threshold, often symbolized with theta ($\theta$). Otherwise, the result is 1.

$y=\left\{{\begin{matrix}1&{\mbox{if }}a\geq \theta \\0&{\mbox{if }}a<\theta \end{matrix}}\right.$

Ramping function

The ramping function is also a piecewise defined function, which can be defined as:

Failed to parse (syntax error): {\displaystyle y = \left\{ \begin{matrix} 0 & \mbox{if }a<0 \\ a & \mbox{if } a \ge 0 \\ 1 & \mbox{if }a \ge 1 \end{matrix}}

Sigmoid

The sigmoid function is used to produce continuous values. It's an S-shaped curve, and it's used when the inputs are between 0 and 1.

$\sigma \left(a\right)={\frac {1}{1+\exp {\bigg (}{\frac {-a-\theta }{\rho }}{\bigg )}}}$

Where $a$ is the activation, $\theta$ is the threshold (that can be zero, simplifying the equation), and $\rho$ is a value which defines the curvature of the sigmoid.

Hyperbolic Tangent

The hyperbolic tangent is an hyperbolic trigonometric function, used when the activation values are between -1 and 1. Its shape is very similar to the shape of the sigmoid.

Impulse pass

Depending on the network model, neurons can pass their impulses to their terminals, or backwards. The "backward pass" can be observed in learning algorithms like "Backpropagation".

Analogy to Biological Neurons

In biological neurons there is a similar behavior. Inputs are electrical pulses transmitted to the synapses (terminals in the dendrites). Electrical pulses produce a release of neurotransmitters which may alter the dendritic membrane potential (Post Synaptic Potential). The Post Synaptic Potential travels over the axon, reaching another neuron, which will sum all the Post Synaptic Potentials received, and fire an output if the total sum of the Post Synaptic Potentials in the axon hillock received exceeds a threshold.