Gravitational lens: Difference between revisions
imported>Jori Liesenborgs (First version of the history section) |
imported>Jori Liesenborgs No edit summary |
||
| Line 5: | Line 5: | ||
|} | |} | ||
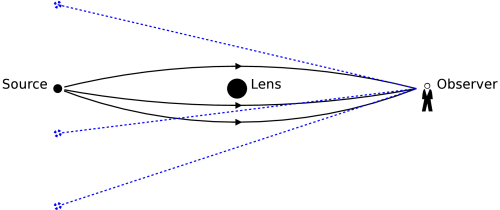
In a gravitational lensing scenario, light traveling from a distant astronomical source (e.g. a galaxy) to | In a gravitational lensing scenario, light traveling from a distant astronomical source (e.g. a [[galaxy]]) to | ||
an observer is deflected by the gravitational field of an intermediate object (e.g. a cluster of | an observer is deflected by the gravitational field of an intermediate object (e.g. a cluster of | ||
galaxies), therefore designated the gravitational lens. Because of this, the observer will see the source | galaxies), therefore designated the gravitational lens. Because of this, the observer will see the source | ||
| Line 20: | Line 20: | ||
|} | |} | ||
In | In [[Newton]]ian mechanics, the path of a test particle in a gravitational field does not depend on the | ||
mass of the test particle. For this reason, one can argue that even in the absolute space and time of | mass of the test particle. For this reason, one can argue that even in the absolute space and time of | ||
Newton, light does not always go in a straight line, but can be deflected | Newton, light does not always go in a straight line, but can be deflected noticeably by objects with a | ||
sufficiently strong gravitational field. In 1804, J. von Soldner was the first one to publish the | sufficiently strong gravitational field. In 1804, J. von Soldner was the first one to publish the | ||
Newtonian value of the deflection angle: | Newtonian value of the deflection angle: | ||
| Line 28: | Line 28: | ||
<math>\hat\alpha_{Newtonian} = \frac{2 G M}{c^2 d}</math> | <math>\hat\alpha_{Newtonian} = \frac{2 G M}{c^2 d}</math> | ||
In this equation, ''G'' is the gravitational constant, ''M'' the mass of the object deflecting the light, ''c'' is | In this equation, ''G'' is the [[gravitational constant]], ''M'' the mass of the object deflecting the light, ''c'' is | ||
the speed of light and ''d'' is the impact parameter of the light ray. | the [[speed of light]] and ''d'' is the impact parameter of the light ray. | ||
More than a century later, after having completed his [[general theory of relativity]], [[Albert Einstein]] published a new expression, differing only by a factor of two from the Newtonian result: | More than a century later, after having completed his [[general theory of relativity]], [[Albert Einstein]] published a new expression, differing only by a factor of two from the Newtonian result: | ||
Revision as of 05:39, 24 February 2007
In a gravitational lensing scenario, light traveling from a distant astronomical source (e.g. a galaxy) to an observer is deflected by the gravitational field of an intermediate object (e.g. a cluster of galaxies), therefore designated the gravitational lens. Because of this, the observer will see the source in a direction different from the one in which the source would be observed if the gravitational lens were absent. Furthermore, it is possible for light rays to reach the observer by multiple paths, causing multiple images of the same source to appear.
History
In Newtonian mechanics, the path of a test particle in a gravitational field does not depend on the mass of the test particle. For this reason, one can argue that even in the absolute space and time of Newton, light does not always go in a straight line, but can be deflected noticeably by objects with a sufficiently strong gravitational field. In 1804, J. von Soldner was the first one to publish the Newtonian value of the deflection angle:
In this equation, G is the gravitational constant, M the mass of the object deflecting the light, c is the speed of light and d is the impact parameter of the light ray.
More than a century later, after having completed his general theory of relativity, Albert Einstein published a new expression, differing only by a factor of two from the Newtonian result:
For a light ray passing close to the sun, the value of this angle is 1.74 arcsec. During a solar eclipse, the bending angle can be calculated by comparing the positions of stars close to the sun to the positions where one would expect these stars to be seen if their light rays were not deflected by the sun. In 1919, a team of astronomers led by Eddington set out to measure the deflection angle during a total eclipse and reported an agreement with Einstein's predicted value with 20% uncertainty. Later measurements drastically reduced this amount of uncertainty to a value of 0.02%.
After this, gravitational deflection of light received only little attention for a very long time. Around 1964 Liebes and especially Refsdal revived the gravitational lens effect briefly, but it wasn't until the first actual gravitationally lensed quasar QSO 0957+561 was observed in 1979 that the subject gained much interest. Since then, a huge amount of articles about gravitational lensing have been published.