Cent (music): Difference between revisions
imported>John R. Brews (source) |
mNo edit summary |
||
| (27 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
{{subpages}} | {{subpages}} | ||
The '''cent''' is a logarithmic measure of a musical interval introduced by Alexander Ellis. | {{TOC|right}} | ||
The '''cent''' is a logarithmic measure of a musical interval introduced by Alexander Ellis. A cent is the logarithmic division of the equitempered [[Semitone (music)|semitone]] into 100 equal parts. | |||
==Formula== | |||
In terms of a formula, the separation or interval between two frequencies ƒ<sub>1</sub> and ƒ<sub>2</sub> in ''cents'' is determined as: | |||
:<math> c = 1200 \log _2 \left( \frac {f_1}{f_2} \right) \ . </math> | |||
Consequently, two frequencies ƒ<sub>1</sub> and ƒ<sub>2</sub> separated by an interval of 1 cent are in the ratio: | |||
:<math>\frac{f_1}{f_2}=2^{1/1200} \approx 1.005777895 \ , </math> | |||
that is, by a ratio given by the 1200th root of 2. | |||
==Background== | |||
The ''cent'' appears in an article Alexander Ellis published in 1885<ref name=tune/> and also in an appendix he added to his translation of [[Herman von Helmholtz]]'s ''Die Lehre von den Tonempfindungen'' published in translation as ''On the Sensation of Tone As a Physiological Basis for the Theory of Music'',<ref name=Ellis/> and also as ''On the sensations of tone''.<ref name=sensations/> | |||
{{Image|Audible frequency difference.png|right|250px|Audible difference in frequency Δƒ/ƒ at two sound levels heard in rapid succession ''vs.'' frequency ƒ.<ref name=Seashore/>}} | |||
{{Image|Tuning error.png|right|250px|Average error of nine flutists in playing a note of specified pitch after listening to a pitch ''A''4 <nowiki>=</nowiki> 442 Hz from a piano.<ref name=Ohgushi/>}} | |||
==Sensitivity of the ear== | |||
{{See also|Music perception}} | |||
According to Ellis, when two notes are played together, a difference of 2 cents is noticeable, and a difference of 5 cents is heard as out of tune.<ref name=tune/> | |||
The figure at right indicates a smaller sound level difference is audible when the sounds are louder, and smaller differences also are audible at higher frequencies.<ref name=Seashore/> The ability to distinguish pitches is extremely variable among listeners, increases with intensity, increases with the abruptness in change of tone, improves with the richness of [[Timbre (music)|timbre]],<ref name=Seashore/> and varies with the shape of the [[envelope function|envelope]] of the waveform that turns the tones on and off.<ref name=Hartmann/> | |||
Recent observations suggest errors of 5-15 cents when playing a specific pitch are common, with errors of 20-50 cents for pitches above ''A''7 (the 7th octave, 3 octaves above the octave containing middle ''C''). (See figure at right.) The increased error at higher pitch was traced to a systematic error in the response of auditory nerves in the ear.<ref name=Ohgushi/> | |||
==References== | ==References== | ||
| Line 8: | Line 30: | ||
<ref name=Ellis> | <ref name=Ellis> | ||
{{cite book |title=On the Sensation of Tone As a Physiological Basis for the Theory of Music |author=Herman von Helmholtz |url= http://books.google.com/books?id=wY2fAAAAMAAJ&pg=PA41 |edition=Alexander Ellis translation of 4th German ed |chapter=Footnote, p. 41 and Appendix XX, Section C|year=1912 |publisher=Longmans, Green}} | {{cite book |title=On the Sensation of Tone As a Physiological Basis for the Theory of Music |author=Herman von Helmholtz |url= http://books.google.com/books?id=wY2fAAAAMAAJ&pg=PA41 |edition=Alexander Ellis translation of 4th 1877 German ed |chapter=Footnote, p. 41 and Appendix XX, Section C|year=1912 |publisher=Longmans, Green}} | ||
</ref> | |||
<ref name=Hartmann> | |||
{{cite book |title=Signals, Sound, and Sensation |url=http://books.google.com/books?id=3N72rIoTHiEC&pg=PA443 |pages=p. 443 |author=William M. Hartmann |isbn= 1563962837 |publisher=Springer |year=1997}} | |||
</ref> | |||
<ref name=Ohgushi> | |||
{{cite journal |title=The Relationship between Musical Pitch and Temporal Responses of the Auditory Nerve Fibers |journal=Journal of Physiological Anthropology and Applied Human Science |volume=24 |issue=1 |pages=pp. 99-101 |year=2005 |author=Ohgushi, K and Ano, Y |url=http://www.brainmusic.org/EducationalActivitiesFolder/Ohgushi_pitch2005.pdf }} | |||
</ref> | |||
<ref name=Seashore>{{cite book |url=http://books.google.com/books?id=p9gUknYfpjYC&pg=PA60&lpg=PA60 |pages=p. 60 |chapter=Figure 1 |author=Carl Emil Seashore |title=Psychology of Music |publisher=Courier Dover Publications |edition=Reprint of McGraw-Hill 1938 ed |isbn=0-486-21851-1 |year=1967}} | |||
</ref> | </ref> | ||
| Line 19: | Line 52: | ||
</ref> | </ref> | ||
}} | }}[[Category:Suggestion Bot Tag]] | ||
Latest revision as of 06:01, 26 July 2024
The cent is a logarithmic measure of a musical interval introduced by Alexander Ellis. A cent is the logarithmic division of the equitempered semitone into 100 equal parts.
Formula
In terms of a formula, the separation or interval between two frequencies ƒ1 and ƒ2 in cents is determined as:
Consequently, two frequencies ƒ1 and ƒ2 separated by an interval of 1 cent are in the ratio:
that is, by a ratio given by the 1200th root of 2.
Background
The cent appears in an article Alexander Ellis published in 1885[1] and also in an appendix he added to his translation of Herman von Helmholtz's Die Lehre von den Tonempfindungen published in translation as On the Sensation of Tone As a Physiological Basis for the Theory of Music,[2] and also as On the sensations of tone.[3]
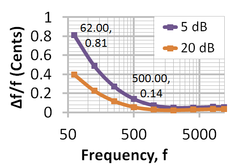
Audible difference in frequency Δƒ/ƒ at two sound levels heard in rapid succession vs. frequency ƒ.[4]
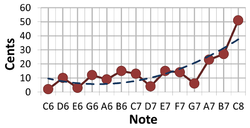
Average error of nine flutists in playing a note of specified pitch after listening to a pitch A4 = 442 Hz from a piano.[5]
Sensitivity of the ear
- See also: Music perception
According to Ellis, when two notes are played together, a difference of 2 cents is noticeable, and a difference of 5 cents is heard as out of tune.[1]
The figure at right indicates a smaller sound level difference is audible when the sounds are louder, and smaller differences also are audible at higher frequencies.[4] The ability to distinguish pitches is extremely variable among listeners, increases with intensity, increases with the abruptness in change of tone, improves with the richness of timbre,[4] and varies with the shape of the envelope of the waveform that turns the tones on and off.[6]
Recent observations suggest errors of 5-15 cents when playing a specific pitch are common, with errors of 20-50 cents for pitches above A7 (the 7th octave, 3 octaves above the octave containing middle C). (See figure at right.) The increased error at higher pitch was traced to a systematic error in the response of auditory nerves in the ear.[5]
References
- ↑ 1.0 1.1 Alexander J Ellis (March 25, 1885). "On the musical scales of various nations; §III.–Cents". Journal of the Society of Arts 33: p. 487.
- ↑ Herman von Helmholtz (1912). “Footnote, p. 41 and Appendix XX, Section C”, On the Sensation of Tone As a Physiological Basis for the Theory of Music, Alexander Ellis translation of 4th 1877 German ed. Longmans, Green.
- ↑ Herman von Helmholtz (1954). On the sensations of tone, Reprint of 1885 translation by Alexander Ellis. Courier Dover Publications. ISBN 0486607534.
- ↑ 4.0 4.1 4.2 Carl Emil Seashore (1967). “Figure 1”, Psychology of Music, Reprint of McGraw-Hill 1938 ed. Courier Dover Publications, p. 60. ISBN 0-486-21851-1.
- ↑ 5.0 5.1 Ohgushi, K and Ano, Y (2005). "The Relationship between Musical Pitch and Temporal Responses of the Auditory Nerve Fibers". Journal of Physiological Anthropology and Applied Human Science 24 (1): pp. 99-101.
- ↑ William M. Hartmann (1997). Signals, Sound, and Sensation. Springer, p. 443. ISBN 1563962837.

