Special relativity: Difference between revisions
imported>John R. Brews mNo edit summary |
mNo edit summary |
||
| (68 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
{{subpages}} | {{subpages}} | ||
{{Image|Classical mechanics timeline.PNG|right|325px|Timeline for key scientists in [[classical mechanics]]}} | |||
{{TOC|right}} | |||
The theory of '''special relativity''' was developed by [[Albert Einstein]] | The [[physics]] theory of '''special relativity''', which was published in 1905, was developed by [[Albert Einstein]] and [[Hendrik Lorentz]] with significant contributions from [[Henri Poincaré]]. The theory describes the behavior of objects traveling at very high speeds - close to the [[speed of light]] in [[classical vacuum|vacuum]] - as determined with inertial reference systems. A prediction of the theory is that when the speed of an object is an appreciable fraction of the speed of light, [[time]] passes at a slower rate for that object. [[Length]]s also vary as the length of an object shortens in the direction of motion. | ||
The increase of [[mass]] was the first prediction of Lorentz and Einstein to be tested. Some early experiments appeared to show a slightly different mass increase; however, improved experiments agreed with the new theory. | |||
Special relativity builds on Maxwell's theory according to which light and other electromagnetic radiation propagate like waves. The speed of a wave is assumed to be fully independent of the motion of the emitter, and experiments supported this feature of light propagation. A postulate of the theory is therefore that the speed of light in vacuum is a constant (its value is denoted by the symbol c), independent of the speed of the source. But unlike the 'classical' example of a sound wave from a train (in which the speed of the air plays a role), the speed of a light wave is always measured as c. Consequently no "light medium" or [[ether (physics)|ether]] velocity can be determined, and any inertial reference system is equally valid as reference for measurements of physics. This is called the relativity postulate. | |||
The theory | The new theory had little effect upon humans' intuitive view of the everyday world; however, our perception of time and distance, while quite correct in everyday life, improperly extends these intuitive ideas to high speeds. Our intuitive understanding from low speed experiences (leading to the 'classical' concepts) is not correct. | ||
The theory of relativity opened up basic questions about measuring intervals in space and time, and revolutionized the description of the physical universe. Electromagnetic signals propagate at the speed of light, and a consequence of the theory is that no particles can go as fast as light. One might ask whether the other forces of nature: weak, strong, gravitational, could provide a form of communication that might be faster; if so, that would break the relativity postulate. Other proposals involve apparent quantum-mechanical nonlocal interactions, but although they seem to allow instant connections between different locations, they certainly don't allow communication.<ref name=Kaku group =Note/> | |||
==Early development of the theory== | |||
Special relativity was developed in view of the null results of certain 19th century physical experiments that attempted to detect the velocity of universe's background [[ether (physics)|ether]], which was supposed to be the ultimate neutral background, or [[reference framework]], against which the entire physical universe moved. Maxwell assumed that this velocity could be determined by a certain experiment which was performed after his death by [[Michelson-Morley experiment|Michelson and Morley]] in 1887-- however, the experiment failed to detect a significant signal, to everyone's surprise. The Michelson-Morley experiment aimed to determine the velocity of light relative to the background ether by means of a specially built [[interferometer]]. It was hoped that this instrument would detect phase differences depending on the paths of two light beams through the ether while the instrument was slowly rotated. During rotation, the differences in light path lengths would show up as a changing light pattern. | |||
As an explanation for that unexpected "null result", Lorentz and Fitzgerald proposed independently that objects (such as interferometers) change shape due to their speed through the ether, masking the effect that was sought. In fact, the experiment was based on the assumption that the shape of objects is totally unaffected by speed. Although that assumption was in agreement with classical mechanics, it was not likely to be correct since already at that time it was known that objects are held together by electromagnetic bonds - which according to Maxwell's theory are affected by speed through the ether. Heaviside calculated in 1888 that the electric field of a charged particle is flattened by - as it later was called - the Lorentz contraction factor. Lorentz found that if indeed the apparatus contracts by that factor, this would exactly nullify the expected effect. | |||
But also other types of experiments failed to detect any speed relative to the ether. | |||
In view of those results, Poincaré suggested in 1900 and more specifically in 1904 that a new theory should be developed according to which the classical relativity principle is also valid for electromagnetic phenomena, so that no physical experiment can discriminate between a state of uniform motion and a state of rest. In this "new mechanics", inertia would be increasing with the velocity, so that the velocity of light would become an impassable limit.<ref name=Poincare=Note> | |||
"Perhaps, too, we shall have to construct an entirely new mechanics that we only succeed in catching a glimpse of, where, inertia increasing with the velocity, the velocity of light would become an impassable limit. The ordinary mechanics, more simple, would remain a first approximation, since it would be true for velocities not too great, so that the old dynamics would still be found under the new." - https://en.wikisource.org/wiki/The_Principles_of_Mathematical_Physics#Future_Mathematical_Physics. | |||
</ref> | |||
Lorentz responded to that request with a paper in 1904 that attempted to obtain this goal. However, although it already contained the correct system transformations, there was a glitch in one of his electromagnetic equations so that the result was not altogether perfect. | |||
This error was quickly corrected by Poincaré and in June 1905 he published a paper in which he announced that Lorentz had managed to obtain a theory in accord with the postulate of the complete impossibility of determining absolute motion. In that paper he also presented what he called the "transformations of Lorentz" in their modern, symmetrical form. | |||
However, Poincaré's correction to the electromagnetic equations was only published in 1906. As a result, although the Lorentz transformations had been first published by Lorentz and Poincaré, it was Einstein who first published the Lorentz transformations together with the full set of correct electromagnetic equations. And in that paper of September 1905, Einstein also presented a more elegant derivation of the new theory as well as elaborate descriptions and corresponding predictions of the Doppler effect and time dilation. And while Lorentz used an ether model as part of the derivation, Einstein avoided referral to such an absolute background in his derivation and only referred to observable objects. | |||
A few other physicists such as Joseph Larmor also made contributions to the development of the theory. | |||
==Einstein's assumptions== | ==Einstein's assumptions== | ||
Einstein | Einstein based his derivation on two postulates. He assumed that physical experiments performed in any room moving at any constant speed in any constant direction, that is, in any [[inertial frame]], must always produce the same results.<ref name=Michelson group=Note/> In other words, ''all'' physical laws should take the same form in all inertial frames, including the [[Maxwell's equations|laws of electromagnetism]].<ref name=Special group=Note/> This notion is shared by [[Classical_mechanics#Newton.27s_laws_of_motion|Newton's laws]] and the mechanics of Galileo, but those formulations considered only mechanical behavior because electromagnetism was not yet known. | ||
Along with this ''relativity postulate'' (which Einstein later called the ''Special principle of relativity''), Einstein also raised to postulate the observation that the speed of light in vacuum is a constant that is independent of the speed of the source.<ref name=Speed group=Note/> | |||
As a consequence of the two postulates taken together, the speed of light in vacuum should be the same for all inertial observers - it is [[invariant]]. | |||
The speed of light is independent of the speed of the source or the observer, but the ''color'' of perceived light does change with the speed of the source or the observer, a phenomenon called the [[Doppler_effect#Absolute_motion|Doppler effect]]. | |||
Although seemingly inconsistent with intuition, assuming the invariance of light's speed actually does not contradict human perception in any obvious way. In everyday life we experience light's speed as invariably infinite: turn on a light switch and a room is illuminated instantaneously. Simple reflection, however, reveals the strangeness of an invariant light speed: | |||
Imagine driving a car straight down a highway at 60 mph. An observer on the side of the road measures our speed at 60 mph. If another car comes toward us at 50 mph as measured by the observer on the side of the road, we inside our car would perceive it coming at us at (60 + 50) = 110 mph. Both cars and the outside observer are in inertial frames. From experience, we know that speeds simply add together. Now imagine that we turn on our headlights. Designating the speed of light in the traditional manner by the symbol ''c'', we see the light beam travel away from us at light's constant speed ''c''. We might also presume that the oncoming car's driver sees our light beam traveling at (''c'' + 110) | Imagine driving a car straight down a highway at 60 mph. An observer on the side of the road measures our speed at 60 mph. If another car comes toward us at 50 mph as measured by the observer on the side of the road, we inside our car would perceive it coming at us at {{nowrap|(60 + 50)}} = {{nowrap|110 mph.}} Both cars and the outside observer are in inertial frames. From experience, we know that speeds simply add together. Now imagine that we turn on our headlights. Designating the speed of light in the traditional manner by the symbol ''c'', we see the light beam travel away from us at light's constant speed ''c''. We might also presume that the oncoming car's driver sees our light beam traveling at {{nowrap|(''c'' + 110 mph)}} because experience tells us we must add the speed of our car and that of the oncoming car to the speed of our light beam. Our assumption that observers always measure light's speed as the same, however, means that the other car determines the light beam moving at speed ''c'' just as we do, and that the extra 110 mph makes no difference. The observer on the side of the road must also see our light beam traveling at speed ''c'' even though it emanates from a moving car. The cars' speeds make no difference. If both cars were traveling at half the speed of light, the oncoming car would still measure our light beam as traveling at speed ''c'', not at {{nowrap|''c'' + (1/2) ''c'' + (1/2) ''c'',}} regardless of the great speed of the two cars. | ||
==Time dilation== | ==Time dilation== | ||
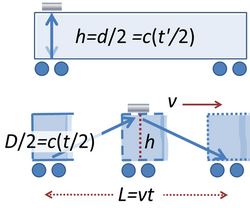
Consider | Consider a [[thought experiment]].<ref name=Taylor group=Note/> We travel in a train uniformly in one direction at speed ''v'' (that is, we're in an inertial frame). An observer stands motionless on the side of the tracks watching our train coach pass (that is, he's also in an inertial frame). We shoot a light beam from a flashlight straight up at a mirror on the train coach's ceiling a distance ''h'' from the flashlight. Inside the train we see the light beam go straight up, hit the mirror, and come straight back down, covering the distance ''h'' twice, which is a total distance of 2''h''. Let's call the short amount of time this experiment takes ''t' ''. During time ''t' '' the train travels a short distance. | ||
{{Image|Light path on train.png|right| | {{Image|Light path on train.png|right|250px|''Top'': View of the light beam's path from inside the train. ''Bottom'': View of the light beam's path from outside the train.}} | ||
Now consider what the observer on the side of the tracks sees. Because the train moves, he does not see the light beam go straight up and down, but sees it climb at an angle, hit the mirror, then travel back down at the same angle to hit the flashlight which has now moved a short distance ''L''. It is worth noting that while the observer on the train can use the same clock to register departure and return, the observer on the track must use ''two'' clocks because the departure and return of the light occur at two separated locations. | Now consider what the observer on the side of the tracks sees. Because the train moves, he does not see the light beam go straight up and down, but sees it climb at an angle, hit the mirror, then travel back down at the same angle to hit the flashlight which has now moved a short distance ''L''. It is worth noting that while the observer on the train can use the same clock to register departure and return, the observer on the track must use ''two'' clocks because the departure and return of the light occur at two separated locations. | ||
On the track, each leg of the light beam's journey is a distance greater than ''h'', so the light has traveled a distance greater than the 2''h'' we measured inside the train. To make this point, imagine a line coming down from the mirror forming a right triangle one of whose sides is the mirror's height ''h'' and the other side half the distance traveled, say ''L''/2. By the [[Pythagorean theorem]], the hypotenuse must be greater than ''h'', in fact √(''h''<sup>2</sup>+(''L''/2)<sup>2</sup>), so the total distance traveled must be greater from the track observer's point of view. | On the track, each leg of the light beam's journey is a distance greater than ''h'', so the light has traveled a distance greater than the 2''h'' we measured inside the train. To make this point, imagine a line coming down from the mirror forming a right triangle one of whose sides is the mirror's height ''h'' and the other side half the distance traveled, say ''L''/2. By the [[Pythagorean theorem]], the hypotenuse must be greater than ''h'', in fact {{nowrap|√(''h''<sup>2</sup>+(''L''/2)<sup>2</sup>),}} so the total distance traveled must be greater from the track observer's point of view. | ||
Let's call the total distance we saw the light beam travel aboard the train ''d'' and the track observer's greater distance ''D''. According to the track observer, suppose the time the experiment took on the train is ''t' '', but for those on the track it is ''t''. The light beam's speed is the same on or off the train, ''c''. | Let's call the total distance we saw the light beam travel aboard the train ''d'' and the track observer's greater distance ''D''. According to the track observer, suppose the time the experiment took on the train is ''t' '', but for those on the track it is ''t''. The light beam's speed is the same on or off the train, ''c''. | ||
| Line 39: | Line 64: | ||
::<math>D = ct \ .</math> | ::<math>D = ct \ .</math> | ||
Because ''d < D'' and ''c'' is constant, we must conclude that ''t' '' < ''t'', that is, from the track observer's viewpoint, the train observers see a shorter time interval than is seen from the track. | Because {{nowrap|''d < D''}} and ''c'' is constant, we must conclude that {{nowrap|''t' '' < ''t'',}} that is, from the track observer's viewpoint, the train observers see a shorter time interval than is seen from the track. | ||
The time relationship is made quantitative using the triangles in the lower panel of the figure. We note that the height of the right triangle is ''h=ct' ''/2, the base is ''vt''/2 and the hypotenuse is ''ct''/2, so using Pythagoras theorem: | The time relationship is made quantitative using the triangles in the lower panel of the figure. We note that the height of the right triangle is ''h=ct' ''/2, the base is ''vt''/2 and the hypotenuse is ''ct''/2, so using Pythagoras theorem: | ||
| Line 45: | Line 70: | ||
or, | or, | ||
:<math>t = t^\prime \ \frac{1}{\sqrt{1-v^2/c^2}} \ , </math> | :<math>t = t^\prime \ \frac{1}{\sqrt{1-v^2/c^2}} \ , </math> | ||
with ''t'' the time on the track, and ''t' '' the time on the train. Evidently, the square root is smaller than ''1'' and so ''t'' >''t' '', as previously concluded. | with ''t'' the time on the track, and ''t' '' the time on the train. Evidently, the square root is smaller than ''1'' and so {{nowrap|''t'' >''t' '',}} as previously concluded. | ||
Of course, the same experiment can be done on the track. Then the light goes vertically up and down according to the track observer, who uses one clock, but follows a triangular path as seen by us on the train using two clocks. By the same reasoning, to us on the train the observers on the track observe a shorter time interval than we do on the train. Thus, the situation is symmetric, and whichever observer is perceived as performing the experiment while apparently moving also is perceived to measure a shorter time interval between the events. | Of course, the same experiment can be done on the track. Then the light goes vertically up and down according to the track observer, who uses one clock, but follows a triangular path as seen by us on the train using two clocks. By the same reasoning, to us on the train the observers on the track observe a shorter time interval than we do on the train. Thus, the situation is symmetric, and whichever observer is perceived as performing the experiment while apparently moving also is perceived to measure a shorter time interval between the events. | ||
This example can be converted to a comparison of clocks. Let's use the flashlight and mirror as a clock. Suppose that a unit of time is that for the light to go from the flashlight to the mirror and back. The same clock construction is used on the train and on the track. Both the clock on the track and that on the train consider one unit of time to be ''2h/c'', and ''h'' and ''c'' are the same for both. But to those on the track watching the traveling clock, the traveling clock on the train counts one unit of time as the longer time Δ''t' ''= 2√(''h''<sup>2</sup>+(''L''/2)<sup>2</sup>)/''c''. Thus, the experiment of watching the clock on the train tick a unit of time takes a time Δ''t' '' according to those on the track. | This example can be converted to a comparison of clocks. Let's use the flashlight and mirror as a clock.<ref name=Feynman group=Note/> Suppose that a unit of time is that for the light to go from the flashlight to the mirror and back. The same clock construction is used on the train and on the track. Both the clock on the track and that on the train consider one unit of time to be ''2h/c'', and ''h'' and ''c'' are the same for both. But to those on the track watching the traveling clock, the traveling clock on the train counts one unit of time as the longer time Δ''t' ''= {{nowrap|2√(''h''<sup>2</sup>+(''L''/2)<sup>2</sup>)/''c''.}} Thus, the experiment of watching the clock on the train tick a unit of time takes a time Δ''t' '' according to those on the track. | ||
On the track, two clocks are used to observe the single clock on the train. To synchronize the two clocks, a light signal is sent to the distant clock and the distant clock is synchronized by setting it so that when the light arrives the time there is ''L/c'', where ''L = v''Δ''t' '' is the clock separation, and Δ''t' '' is the time of the experiment (according to those on the track). The height ''h'' on the other hand is ''h=c''Δ''t''/2 according to their clock. Substituting: | On the track, two clocks are used to observe the single clock on the train. To synchronize the two clocks, a light signal is sent to the distant clock and the distant clock is synchronized by setting it so that when the light arrives the time there is ''L/c'', where ''L = v''Δ''t' '' is the clock separation, and Δ''t' '' is the time of the experiment (according to those on the track). The height ''h'' on the other hand is ''h=c''Δ''t''/2 according to their clock. Substituting: | ||
:<math>\Delta t^\prime =\frac{1}{c}\sqrt{(2h)^2 + L^2} = \frac{1}{c} \sqrt{ (c\Delta t)^2 + (v \Delta t^\prime)^2} </math> | :<math>\Delta t^\prime =\frac{1}{c}\sqrt{(2h)^2 + L^2} = \frac{1}{c} \sqrt{ (c\Delta t)^2 + (v \Delta t^\prime)^2} </math> | ||
::<math>= \frac{\Delta t}{\sqrt{1-v^2/c^2}} \ ,</math> | ::<math>= \frac{\Delta t}{\sqrt{1-v^2/c^2}} \ ,</math> | ||
which is to say the clock on the train appears to run slower than the clock on the track because the unit of time on the train appears longer. Because the unit of time is longer on the train according to those on the track, the separation in time of two events as measured on the train appears to be shorter than | which is to say the clock on the train appears to run slower than the clock on the track because the unit of time on the train appears longer. Because the unit of time is longer on the train according to those on the track, the separation in time of two events as measured on the train appears to be shorter than when observed from the track, which is how this example started out. | ||
Again, the same comparison of time units can be done from the train observer's viewpoint, for whom the clock on the track is moving. For the train observer, the clock on the track runs slower. | Again, the same comparison of time units can be done from the train observer's viewpoint, for whom the clock on the track is moving. For the train observer, the clock on the track runs slower. | ||
This slow-down of clocks perceived to be moving is called ''time dilation''. | This slow-down of clocks perceived to be moving is called ''time dilation''. | ||
==Lorentz contraction== | |||
Let the length of the coach be ''L<sub>0</sub>'' as measured by those on the train by sending a light signal from one end of the car to the other and reflecting it back: | |||
:<math>L_0 = c\tau/2 \ , </math> | |||
where τ is the time of the round trip. For those on the track, this time is too short because moving clocks run slow, and on the track this time is seen as {{nowrap|τ/√(1-''v''<sup>2</sup>/''c''<sup>2</sup>).}} But the time seen by those on the track can be calculated as follows: let the time for the outward signal to reach the mirror at the end of the coach be ''t<sub>1</sub>''. Then the outward light signal travels a distance {{nowrap|''L'' + ''vt''<sub>1</sub>}} as the mirror retreats from the source a distance ''vt''<sub>1</sub>, where ''L'' is length of the coach according to those on the track. Accordingly: | |||
:<math> t_1 = (L+vt_1)/c \ , </math> | |||
or, solving for the time: | |||
:<math> t_1=\frac{L/c}{1-v/c} \ . </math> | |||
In the same way, the reflected return light signal travels a distance {{nowrap|''L − vt''<sub>2</sub>}} as the receiving point moves toward the return signal an amount ''vt''<sub>2</sub>. The time ''t''<sub>2</sub> is then: | |||
:<math> t_2 = \frac{L/c}{1+v/c} \ . </math> | |||
Adding the times produces:<ref name=algebra group=Note/> | |||
:<math> t_1+t_2 = \frac{2L/c}{1-v^2/c^2} = \frac{\tau}{\sqrt{1-v^2/c^2}} \ , </math> | |||
or: | |||
:<math> L = \frac{c \tau}{2} \sqrt{1-v^2/c^2} = L_0 \sqrt{1-v^2/c^2} \ . </math> | |||
In words, the length seen on the track is smaller than the length seen on the train, a phenomenon called ''Lorentz contraction''. The frame where the coach appears to be stationary (that is, the frame of the moving train) is called the ''rest frame'' of the coach because it doesn't move in this frame, so to restate matters, the Lorentz contraction always makes the dimension of a moving object measured in the direction of its motion less than that dimension in its rest frame. | |||
==Lorentz transformation== | ==Lorentz transformation== | ||
Time dilation specifies that time passes more slowly in an inertial frame that moves relative to our own, countering human perception of time's universally uniform passage. Time's passage, however, differs infinitesimally even well beyond the top speeds humans can achieve with the help of technology such as rocket propulsion. To calculate the magnitude of time dilation and the relativistic effect on length in the direction of motion, | Time dilation specifies that time passes more slowly in an inertial frame that moves relative to our own, countering human perception of time's universally uniform passage. Time's passage, however, differs infinitesimally even well beyond the top speeds humans can achieve with the help of technology such as rocket propulsion. To calculate the magnitude of time dilation and the relativistic effect on length in the direction of motion, special relativity employs the [[Inertial_frame_of_reference#Lorentz_frames_of_reference|Lorentz transformation]] first proposed by [[Hendrik Antoon Lorentz]]. He discovered that when the following substitutions were made in [[Maxwell equations|Maxwell's equations]], their form remained the same: | ||
:<math>x^\prime=\frac{x-vt}{\sqrt{1-v^2/c^2}} \ , </math> | |||
:<math>y^\prime=y \ , </math> | |||
:<math>z^\prime=z \ , </math> | |||
:<math>t^\prime =\frac{t-vx/c^2}{\sqrt{1-v^2/c^2}} \ . </math> | |||
These equations are known as the ''Lorentz transformation'' in one dimension. | |||
Newton's laws do not retain the same form under these substitutions, and their modification to resolve this discrepancy leads to special relativity. Of course, the question arose historically which had to be changed: Newton's laws or Maxwell's equations? Einstein showed that, in a universe where communication was limited to take place no faster than the speed of light, simple arguments about synchronizing clocks and measuring distances suggested it was Newton's laws that had to be changed. | |||
To compare common-sense with the Lorentz transformation, consider first a common sense scenario. Suppose that we are motionless with our clock in an inertial frame (the ''reference frame'') as a car with its own clock passes by in its inertial frame (the ''primed frame'') at velocity ''v''. The car's length, which we measured beforehand as ''L'', is measured by its driver in the car's inertial frame as ''L' ''. If, according to our clock, we time an interval ''t'' after the car passes us, we know from experience the car's clock will also have passed the same time ''t''. If we measure the car's length as it goes by, our common sense and measuring technique also gives us length ''L''. The formulas ''t''' = ''t'' and ''L' '' = ''L'' follow from the [[Inertial_frame_of_reference#Galilean_frames_of_reference|Galilean transformation]]: | |||
:<math>x^\prime=x-vt \ , </math> | |||
:<math>y^\prime=y \ , </math> | |||
:<math>z^\prime=z \ , </math> | |||
:<math>t^\prime =t \ . </math> | |||
which is the same as the Lorentz transformation with the ratio {{nowrap|''v/c''<nowiki>=</nowiki>0.}} | |||
As we have already seen, though, | As we have already seen, though, special relativity's effects elude our common-sense perception, so to calculate the change in time and length we now use formulas following from the Lorentz transformation, which lead to the phenomena of time dilation and Lorentz contraction described above. | ||
For human scaled velocities – always infinitesimal relative to the speed of light – the fraction {{nowrap|''v''<sup>2</sup>/''c''<sup>2</sup>}} is so close to zero that the quantity under the square root in the Lorentz formulas is effectively ''1''. Since the square root of ''1'' is ''1'', we can see these formulas reduce to those conforming to common sense, which tells us time passes uniformly and object's length doesn't vary just from an object's uniform velocity, in accord with the formulas from the Galilean transformation. Should ''v'', however, become an appreciable fraction of ''c'', the ratio {{nowrap|''v''<sup>2</sup>/''c''<sup>2</sup>}} gets closer to ''1'' so {{nowrap|√(''1'' - ''v''<sup>2</sup>/''c''<sup>2</sup>)}} gets close to zero. Thus, the Lorentz transformation departs significantly from the Galilean transformation at speeds approaching the speed of light. | |||
==Simultaneous events== | |||
The equation: | |||
:<math>t^\prime =\frac{t-vx/c^2}{\sqrt{1-v^2/c^2}} \ , </math> | |||
of the Lorentz transformation has the very important consequence that two observers moving uniformly relative to each other do not agree on the time interval between two events occurring at separated locations. | |||
::<math> | Suppose in the unprimed frame one event occurs at time ''t'' at one location ''x<sub>1</sub>'' and another at the same time ''t'' at a different location ''x<sub>2</sub>''. Then in the primed frame, the first event occurs at time ''t'<sub>1</sub>'': | ||
:<math>t^\prime_1 =\frac{t-vx_1/c^2}{\sqrt{1-v^2/c^2}} \ , </math> | |||
and the second event at ''t'<sub>2</sub>'': | |||
:<math>t^\prime_2 =\frac{t-vx_2/c^2}{\sqrt{1-v^2/c^2}} \ , </math> | |||
so there is a non-zero time interval between these events: | |||
:<math>t^\prime_2-t^\prime_1 =\frac{vx_1/c^2-vx_2/c^2}{\sqrt{1-v^2/c^2}}=\left(x_1-x_2\right)\frac{v/c^2}{\sqrt{1-v^2/c^2}} \ . </math> | |||
In words, two simultaneous events at different locations in one frame of reference are ''not'' simultaneous events in another inertial frame of reference moving along the line joining the locations of the two events. This difference depends upon the ratio ''v/c'', so it is not noticeable at everyday speeds. | |||
This failure of simultaneity is directly related to a moving observer's inability to agree that a stationary observer's clocks are synchronized at different locations. | |||
Consider how synchronization is accomplished. The stationary observer cannot synchronize two separated clocks by carrying one clock to the other, because that involves motion of the clock that will affect its time. Instead, light signals are sent from one clock to the other. If the two clocks are distant ''L'' from each other, the signal leaves the originating clock at time ''t=0'' and arrives at the other at ''t=L/c''. So the receiving clock is set at ''t=L/c'' when the signal arrives. If it is reflected back to the originating clock, it arrives at ''t=2L/c'', confirming the length is correctly determined. | |||
But, as noted above, another observer moving relative to the first along the line joining the clocks will not agree that the distance is ''L'' because of the Lorentz contraction. So the moving observer will conclude the clocks of the other are not synchronized properly. So, naturally, the moving and stationary observers also will not agree upon the time difference between events seen at the two locations. | |||
==The twin paradox== | ==The twin paradox== | ||
| Line 84: | Line 150: | ||
The details in resolving the paradox go beyond this article's scope. Suffice it to say that the twins are subject to relative acceleration and thus do not remain at all times in two frames that are related as inertial frames. Acceleration implies departure from an inertial frame, and Special Relativity regards only the laws of physics in inertial frames. Once forces like acceleration (or deceleration) or gravity are introduced, one must turn to the [[Theory of General Relativity]] to explain motion's effects on length and the passage of time. | The details in resolving the paradox go beyond this article's scope. Suffice it to say that the twins are subject to relative acceleration and thus do not remain at all times in two frames that are related as inertial frames. Acceleration implies departure from an inertial frame, and Special Relativity regards only the laws of physics in inertial frames. Once forces like acceleration (or deceleration) or gravity are introduced, one must turn to the [[Theory of General Relativity]] to explain motion's effects on length and the passage of time. | ||
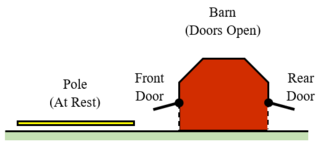
==The pole-in-the-barn paradox== | |||
{{Image|SpecialRelativity PoleInBarn 1.png|right|320px|Pole (at rest) and barn}} | |||
The failure of simultaneity in special relativity is illustrated by the [[pole-in-the-barn paradox]]. The scenario includes a long, horizontal pole and a barn with both a front and a rear door, as shown in Figure 8.1. The pole's length is Lp ''in its rest frame'', and the distance between the barn's two doors is Lb < Lp. As such, when at rest the pole cannot fit inside the barn. However, when moving at relativistic speeds, the pole can be shorter than the barn owing to length contraction and will fit inside the barn. For a complete description, see the [[pole-in-the-barn paradox]] article. | |||
==Energy and momentum== | |||
As pointed out, Newton's laws of mechanics are not compatible with the [[Special relativity#Lorentz transformation|Lorentz transformation]] required so that Maxwell's equations keep the same form for all inertial observers, as specified by the first postulate of special relativity. | |||
<ref name=Special group=Note/> Without going into much detail, the changes in Newton's laws are outlined here, and some of their more notable implications. The most amazing aspect of special relativity is the abandonment of absolute time, a fundamental assumption of the Newtonian theory, and special relativity's introduction of space and time as being interconnected. This aspect has been explained at length above. | |||
These ideas mean that Newton's second law must be expressed as: | |||
:<math>\boldsymbol F = \frac{d}{dt}\left( m \boldsymbol v \right ) \ , </math> | |||
which states in words that force is the rate of change of momentum. The above form of the law is ''not'' changed (although its often-stated form that force is mass times acceleration is not equivalent), but the ''mass'' changes: | |||
:<math>m = \frac{m_0}{\sqrt{1-v^2/c^2}} \ , </math> | |||
where the symbol ''m<sub>0</sub>'' represents the ''rest mass'' of a body, that is, its mass as seen a frame of reference where it is stationary, and the symbol ''m'' is now the ''relativistic mass'', the mass of the body seen in a frame where the mass is moving at a constant speed ''v''. | |||
This formula for mass can be rearranged by using the smallness of the ratio ''v/c'' to expand the square root as a series in this ratio: | |||
:<math>\sqrt{1-v^2/c^2} = 1 - \frac{1}{2}v^2/c^2 + \cdots \ . </math> | |||
:<math>mc^2 = m_0c^2\frac{1}{\sqrt{1-v^2/c^2}} = m_0c^2 + \frac{1}{2}m_0v^2 + \cdots \ .</math> | |||
The second term is the kinetic energy of the body, and Einstein interpreted the left side of this equation as the total energy of the body, resulting in the famous expression ''E = mc''<sup>2</sup> that expresses the ability to convert mass into energy, the mechanism underlying [[Nuclear power reconsidered|nuclear power]] generation, as well as Nuclear weapons. | |||
It should be noted that this mass-energy equivalence is not based simply upon the above series expansion, but is inextricably mixed up with the interchangeability of space and time. All physical quantities are no longer vectors in space only, as with Newton's mechanics, but are vectors in space and time, so-called ''four-vectors''. In particular, energy and momentum make up an ''energy-momentum four vector'':<ref name=Pelligrini group=Note/> | |||
:<math>p_i=m_0\gamma v_i \ \ i=1,\ 2, \ 3 \ , </math> | |||
:<math>p_4=m_0\gamma c\ , </math> | |||
where '''''v''''' = {''v''<sub>i</sub>} is the three-vector of velocity of a particle, and with ''γ'' a symbol for: | |||
:<math>\gamma=\frac{1}{\sqrt{1-v^2/c^2}} \ . </math> | |||
The first three components are the space-like components and the fourth component is the time-like component. It is related to the energy, ''E'': | |||
:<math>E = cp_4 = m_0c^2\gamma\ . </math> | |||
==References== | ==References== | ||
{{Reflist|group=Note|refs= | {{Reflist|group=Note|refs= | ||
<ref name=Kaku group =Note> | |||
For example, see the discussion by {{cite book |title=Physics of the impossible: a scientific exploration into the world of phasers, force fields, teleportation, and time travel |author=Michio Kaku |url=http://books.google.com/books?id=ube-MQcFFZQC&pg=PA62 |pages=pp. 62 ''ff'' |isbn= 0385520697 |year=2008 |publisher =Random House Digital Inc.}} | |||
</ref> | |||
<ref name=Special group=Note> | <ref name=Special group=Note> | ||
| Line 105: | Line 203: | ||
<ref name=Taylor group=Note> | <ref name=Taylor group=Note> | ||
This example is very common in the literature of relativity. For example, see {{cite book |title=Classical mechanics |author=John R. Taylor |pages=pp. 603 ''ff'' |chapter=§15.4 The relativity of time; time dilation & Figure 15.3 |publisher=University Science Books |year=2005 |isbn=189138922X |url=http://www.amazon.com/Classical-Mechanics-John-R-Taylor/dp/189138922X/ref=sr_1_1?s=books&ie=UTF8&qid=1317643027&sr=1-1#reader_189138922X}} | This example is very common in the literature of relativity. For example, see {{cite book |title=Classical mechanics |author=John R. Taylor |pages=pp. 603 ''ff'' |chapter=§15.4 The relativity of time; time dilation & Figure 15.3 |publisher=University Science Books |year=2005 |isbn=189138922X |url=http://www.amazon.com/Classical-Mechanics-John-R-Taylor/dp/189138922X/ref=sr_1_1?s=books&ie=UTF8&qid=1317643027&sr=1-1#reader_189138922X}} | ||
</ref> | |||
<ref name=Feynman group=Note> | |||
The use of a "light clock" is introduced by {{cite book |author= RP Feynman |title=The Feynman Lectures on Physics, Volume 1|pages=pp. 15-5 ''ff'' |chapter=§15.4 Transformation of time |year=1963|publisher=Addison-Wesley}} and also {{cite book |title=Six not-so-easy pieces |author = RP Feynman |url=http://www.amazon.com/Six-Not-So-Easy-Pieces-Relativity-Space-Time/dp/0465025269#reader_0465025269 |title=Six not-so-easy pieces |chapter=§3-4 Transformation of time |pages=pp. 59 ''ff'' |isbn=0465025269 |year=2011 |edition=4th ed |publisher=Basic Books |year=2011}} This clock is idealized in that the mechanisms for reflecting the light and detecting its arrival and departure times have not been examined, nor any implications these mechanisms might have upon actual time measurements. If one is not ready to accept the possibility of a viable light clock, an old fashioned pendulum clock can be substituted that swings back and forth in the plane perpendicular to the direction of motion. The argument remains the same. | |||
</ref> | |||
<ref name=algebra group=Note> | |||
The algebra here is as follows. Note the identity: | |||
:<math>(1-v/c)(1+v/c) = 1-v^2/c^2 \ . </math> | |||
Then multiplying top and bottom of fractions by one or the other of the two factors on the left, one can add the two fractions over a common denominator: | |||
:<math>\frac{1}{1+v/c} +\frac{1}{1-v/c} = \frac{1-v/c}{1-v^2/c^2}+\frac{1+v/c}{1-v^2/c^2} = \frac{2}{1-v^2/c^2} \ .</math> | |||
</ref> | </ref> | ||
| Line 112: | Line 222: | ||
</ref> | </ref> | ||
}} | <ref name=Pelligrini group=Note> | ||
For a discussion see, for example, {{cite book |title=Modern analytic mechanics |author=Richard Kent Cooper, Claudio Pellegrini |url=http://books.google.com/books?id=ff5yEtDAvKMC&pg=PA227 |pages=p. 227 |chapter=§9.6 Energy-momentum four-vector |isbn=0306459582 |year=1999 |publisher=Springer }} | |||
</ref> | |||
}}[[Category:Suggestion Bot Tag]] | |||
Latest revision as of 16:01, 20 October 2024
The physics theory of special relativity, which was published in 1905, was developed by Albert Einstein and Hendrik Lorentz with significant contributions from Henri Poincaré. The theory describes the behavior of objects traveling at very high speeds - close to the speed of light in vacuum - as determined with inertial reference systems. A prediction of the theory is that when the speed of an object is an appreciable fraction of the speed of light, time passes at a slower rate for that object. Lengths also vary as the length of an object shortens in the direction of motion.
The increase of mass was the first prediction of Lorentz and Einstein to be tested. Some early experiments appeared to show a slightly different mass increase; however, improved experiments agreed with the new theory.
Special relativity builds on Maxwell's theory according to which light and other electromagnetic radiation propagate like waves. The speed of a wave is assumed to be fully independent of the motion of the emitter, and experiments supported this feature of light propagation. A postulate of the theory is therefore that the speed of light in vacuum is a constant (its value is denoted by the symbol c), independent of the speed of the source. But unlike the 'classical' example of a sound wave from a train (in which the speed of the air plays a role), the speed of a light wave is always measured as c. Consequently no "light medium" or ether velocity can be determined, and any inertial reference system is equally valid as reference for measurements of physics. This is called the relativity postulate.
The new theory had little effect upon humans' intuitive view of the everyday world; however, our perception of time and distance, while quite correct in everyday life, improperly extends these intuitive ideas to high speeds. Our intuitive understanding from low speed experiences (leading to the 'classical' concepts) is not correct.
The theory of relativity opened up basic questions about measuring intervals in space and time, and revolutionized the description of the physical universe. Electromagnetic signals propagate at the speed of light, and a consequence of the theory is that no particles can go as fast as light. One might ask whether the other forces of nature: weak, strong, gravitational, could provide a form of communication that might be faster; if so, that would break the relativity postulate. Other proposals involve apparent quantum-mechanical nonlocal interactions, but although they seem to allow instant connections between different locations, they certainly don't allow communication.[Note 1]
Early development of the theory
Special relativity was developed in view of the null results of certain 19th century physical experiments that attempted to detect the velocity of universe's background ether, which was supposed to be the ultimate neutral background, or reference framework, against which the entire physical universe moved. Maxwell assumed that this velocity could be determined by a certain experiment which was performed after his death by Michelson and Morley in 1887-- however, the experiment failed to detect a significant signal, to everyone's surprise. The Michelson-Morley experiment aimed to determine the velocity of light relative to the background ether by means of a specially built interferometer. It was hoped that this instrument would detect phase differences depending on the paths of two light beams through the ether while the instrument was slowly rotated. During rotation, the differences in light path lengths would show up as a changing light pattern.
As an explanation for that unexpected "null result", Lorentz and Fitzgerald proposed independently that objects (such as interferometers) change shape due to their speed through the ether, masking the effect that was sought. In fact, the experiment was based on the assumption that the shape of objects is totally unaffected by speed. Although that assumption was in agreement with classical mechanics, it was not likely to be correct since already at that time it was known that objects are held together by electromagnetic bonds - which according to Maxwell's theory are affected by speed through the ether. Heaviside calculated in 1888 that the electric field of a charged particle is flattened by - as it later was called - the Lorentz contraction factor. Lorentz found that if indeed the apparatus contracts by that factor, this would exactly nullify the expected effect.
But also other types of experiments failed to detect any speed relative to the ether.
In view of those results, Poincaré suggested in 1900 and more specifically in 1904 that a new theory should be developed according to which the classical relativity principle is also valid for electromagnetic phenomena, so that no physical experiment can discriminate between a state of uniform motion and a state of rest. In this "new mechanics", inertia would be increasing with the velocity, so that the velocity of light would become an impassable limit.[1]
Lorentz responded to that request with a paper in 1904 that attempted to obtain this goal. However, although it already contained the correct system transformations, there was a glitch in one of his electromagnetic equations so that the result was not altogether perfect.
This error was quickly corrected by Poincaré and in June 1905 he published a paper in which he announced that Lorentz had managed to obtain a theory in accord with the postulate of the complete impossibility of determining absolute motion. In that paper he also presented what he called the "transformations of Lorentz" in their modern, symmetrical form.
However, Poincaré's correction to the electromagnetic equations was only published in 1906. As a result, although the Lorentz transformations had been first published by Lorentz and Poincaré, it was Einstein who first published the Lorentz transformations together with the full set of correct electromagnetic equations. And in that paper of September 1905, Einstein also presented a more elegant derivation of the new theory as well as elaborate descriptions and corresponding predictions of the Doppler effect and time dilation. And while Lorentz used an ether model as part of the derivation, Einstein avoided referral to such an absolute background in his derivation and only referred to observable objects.
A few other physicists such as Joseph Larmor also made contributions to the development of the theory.
Einstein's assumptions
Einstein based his derivation on two postulates. He assumed that physical experiments performed in any room moving at any constant speed in any constant direction, that is, in any inertial frame, must always produce the same results.[Note 2] In other words, all physical laws should take the same form in all inertial frames, including the laws of electromagnetism.[Note 3] This notion is shared by Newton's laws and the mechanics of Galileo, but those formulations considered only mechanical behavior because electromagnetism was not yet known.
Along with this relativity postulate (which Einstein later called the Special principle of relativity), Einstein also raised to postulate the observation that the speed of light in vacuum is a constant that is independent of the speed of the source.[Note 4]
As a consequence of the two postulates taken together, the speed of light in vacuum should be the same for all inertial observers - it is invariant.
The speed of light is independent of the speed of the source or the observer, but the color of perceived light does change with the speed of the source or the observer, a phenomenon called the Doppler effect.
Although seemingly inconsistent with intuition, assuming the invariance of light's speed actually does not contradict human perception in any obvious way. In everyday life we experience light's speed as invariably infinite: turn on a light switch and a room is illuminated instantaneously. Simple reflection, however, reveals the strangeness of an invariant light speed:
Imagine driving a car straight down a highway at 60 mph. An observer on the side of the road measures our speed at 60 mph. If another car comes toward us at 50 mph as measured by the observer on the side of the road, we inside our car would perceive it coming at us at (60 + 50) = 110 mph. Both cars and the outside observer are in inertial frames. From experience, we know that speeds simply add together. Now imagine that we turn on our headlights. Designating the speed of light in the traditional manner by the symbol c, we see the light beam travel away from us at light's constant speed c. We might also presume that the oncoming car's driver sees our light beam traveling at (c + 110 mph) because experience tells us we must add the speed of our car and that of the oncoming car to the speed of our light beam. Our assumption that observers always measure light's speed as the same, however, means that the other car determines the light beam moving at speed c just as we do, and that the extra 110 mph makes no difference. The observer on the side of the road must also see our light beam traveling at speed c even though it emanates from a moving car. The cars' speeds make no difference. If both cars were traveling at half the speed of light, the oncoming car would still measure our light beam as traveling at speed c, not at c + (1/2) c + (1/2) c, regardless of the great speed of the two cars.
Time dilation
Consider a thought experiment.[Note 5] We travel in a train uniformly in one direction at speed v (that is, we're in an inertial frame). An observer stands motionless on the side of the tracks watching our train coach pass (that is, he's also in an inertial frame). We shoot a light beam from a flashlight straight up at a mirror on the train coach's ceiling a distance h from the flashlight. Inside the train we see the light beam go straight up, hit the mirror, and come straight back down, covering the distance h twice, which is a total distance of 2h. Let's call the short amount of time this experiment takes t' . During time t' the train travels a short distance.
Now consider what the observer on the side of the tracks sees. Because the train moves, he does not see the light beam go straight up and down, but sees it climb at an angle, hit the mirror, then travel back down at the same angle to hit the flashlight which has now moved a short distance L. It is worth noting that while the observer on the train can use the same clock to register departure and return, the observer on the track must use two clocks because the departure and return of the light occur at two separated locations.
On the track, each leg of the light beam's journey is a distance greater than h, so the light has traveled a distance greater than the 2h we measured inside the train. To make this point, imagine a line coming down from the mirror forming a right triangle one of whose sides is the mirror's height h and the other side half the distance traveled, say L/2. By the Pythagorean theorem, the hypotenuse must be greater than h, in fact √(h2+(L/2)2), so the total distance traveled must be greater from the track observer's point of view.
Let's call the total distance we saw the light beam travel aboard the train d and the track observer's greater distance D. According to the track observer, suppose the time the experiment took on the train is t' , but for those on the track it is t. The light beam's speed is the same on or off the train, c.
Since distance = rate × time we now have
and
Because d < D and c is constant, we must conclude that t' < t, that is, from the track observer's viewpoint, the train observers see a shorter time interval than is seen from the track.
The time relationship is made quantitative using the triangles in the lower panel of the figure. We note that the height of the right triangle is h=ct' /2, the base is vt/2 and the hypotenuse is ct/2, so using Pythagoras theorem:
or,
with t the time on the track, and t' the time on the train. Evidently, the square root is smaller than 1 and so t >t' , as previously concluded.
Of course, the same experiment can be done on the track. Then the light goes vertically up and down according to the track observer, who uses one clock, but follows a triangular path as seen by us on the train using two clocks. By the same reasoning, to us on the train the observers on the track observe a shorter time interval than we do on the train. Thus, the situation is symmetric, and whichever observer is perceived as performing the experiment while apparently moving also is perceived to measure a shorter time interval between the events.
This example can be converted to a comparison of clocks. Let's use the flashlight and mirror as a clock.[Note 6] Suppose that a unit of time is that for the light to go from the flashlight to the mirror and back. The same clock construction is used on the train and on the track. Both the clock on the track and that on the train consider one unit of time to be 2h/c, and h and c are the same for both. But to those on the track watching the traveling clock, the traveling clock on the train counts one unit of time as the longer time Δt' = 2√(h2+(L/2)2)/c. Thus, the experiment of watching the clock on the train tick a unit of time takes a time Δt' according to those on the track.
On the track, two clocks are used to observe the single clock on the train. To synchronize the two clocks, a light signal is sent to the distant clock and the distant clock is synchronized by setting it so that when the light arrives the time there is L/c, where L = vΔt' is the clock separation, and Δt' is the time of the experiment (according to those on the track). The height h on the other hand is h=cΔt/2 according to their clock. Substituting:
which is to say the clock on the train appears to run slower than the clock on the track because the unit of time on the train appears longer. Because the unit of time is longer on the train according to those on the track, the separation in time of two events as measured on the train appears to be shorter than when observed from the track, which is how this example started out.
Again, the same comparison of time units can be done from the train observer's viewpoint, for whom the clock on the track is moving. For the train observer, the clock on the track runs slower.
This slow-down of clocks perceived to be moving is called time dilation.
Lorentz contraction
Let the length of the coach be L0 as measured by those on the train by sending a light signal from one end of the car to the other and reflecting it back:
where τ is the time of the round trip. For those on the track, this time is too short because moving clocks run slow, and on the track this time is seen as τ/√(1-v2/c2). But the time seen by those on the track can be calculated as follows: let the time for the outward signal to reach the mirror at the end of the coach be t1. Then the outward light signal travels a distance L + vt1 as the mirror retreats from the source a distance vt1, where L is length of the coach according to those on the track. Accordingly:
or, solving for the time:
In the same way, the reflected return light signal travels a distance L − vt2 as the receiving point moves toward the return signal an amount vt2. The time t2 is then:
Adding the times produces:[Note 7]
or:
In words, the length seen on the track is smaller than the length seen on the train, a phenomenon called Lorentz contraction. The frame where the coach appears to be stationary (that is, the frame of the moving train) is called the rest frame of the coach because it doesn't move in this frame, so to restate matters, the Lorentz contraction always makes the dimension of a moving object measured in the direction of its motion less than that dimension in its rest frame.
Lorentz transformation
Time dilation specifies that time passes more slowly in an inertial frame that moves relative to our own, countering human perception of time's universally uniform passage. Time's passage, however, differs infinitesimally even well beyond the top speeds humans can achieve with the help of technology such as rocket propulsion. To calculate the magnitude of time dilation and the relativistic effect on length in the direction of motion, special relativity employs the Lorentz transformation first proposed by Hendrik Antoon Lorentz. He discovered that when the following substitutions were made in Maxwell's equations, their form remained the same:
These equations are known as the Lorentz transformation in one dimension.
Newton's laws do not retain the same form under these substitutions, and their modification to resolve this discrepancy leads to special relativity. Of course, the question arose historically which had to be changed: Newton's laws or Maxwell's equations? Einstein showed that, in a universe where communication was limited to take place no faster than the speed of light, simple arguments about synchronizing clocks and measuring distances suggested it was Newton's laws that had to be changed.
To compare common-sense with the Lorentz transformation, consider first a common sense scenario. Suppose that we are motionless with our clock in an inertial frame (the reference frame) as a car with its own clock passes by in its inertial frame (the primed frame) at velocity v. The car's length, which we measured beforehand as L, is measured by its driver in the car's inertial frame as L' . If, according to our clock, we time an interval t after the car passes us, we know from experience the car's clock will also have passed the same time t. If we measure the car's length as it goes by, our common sense and measuring technique also gives us length L. The formulas t' = t and L' = L follow from the Galilean transformation:
which is the same as the Lorentz transformation with the ratio v/c=0.
As we have already seen, though, special relativity's effects elude our common-sense perception, so to calculate the change in time and length we now use formulas following from the Lorentz transformation, which lead to the phenomena of time dilation and Lorentz contraction described above.
For human scaled velocities – always infinitesimal relative to the speed of light – the fraction v2/c2 is so close to zero that the quantity under the square root in the Lorentz formulas is effectively 1. Since the square root of 1 is 1, we can see these formulas reduce to those conforming to common sense, which tells us time passes uniformly and object's length doesn't vary just from an object's uniform velocity, in accord with the formulas from the Galilean transformation. Should v, however, become an appreciable fraction of c, the ratio v2/c2 gets closer to 1 so √(1 - v2/c2) gets close to zero. Thus, the Lorentz transformation departs significantly from the Galilean transformation at speeds approaching the speed of light.
Simultaneous events
The equation:
of the Lorentz transformation has the very important consequence that two observers moving uniformly relative to each other do not agree on the time interval between two events occurring at separated locations.
Suppose in the unprimed frame one event occurs at time t at one location x1 and another at the same time t at a different location x2. Then in the primed frame, the first event occurs at time t'1:
and the second event at t'2:
so there is a non-zero time interval between these events:
In words, two simultaneous events at different locations in one frame of reference are not simultaneous events in another inertial frame of reference moving along the line joining the locations of the two events. This difference depends upon the ratio v/c, so it is not noticeable at everyday speeds.
This failure of simultaneity is directly related to a moving observer's inability to agree that a stationary observer's clocks are synchronized at different locations.
Consider how synchronization is accomplished. The stationary observer cannot synchronize two separated clocks by carrying one clock to the other, because that involves motion of the clock that will affect its time. Instead, light signals are sent from one clock to the other. If the two clocks are distant L from each other, the signal leaves the originating clock at time t=0 and arrives at the other at t=L/c. So the receiving clock is set at t=L/c when the signal arrives. If it is reflected back to the originating clock, it arrives at t=2L/c, confirming the length is correctly determined.
But, as noted above, another observer moving relative to the first along the line joining the clocks will not agree that the distance is L because of the Lorentz contraction. So the moving observer will conclude the clocks of the other are not synchronized properly. So, naturally, the moving and stationary observers also will not agree upon the time difference between events seen at the two locations.
The twin paradox
Notice that the principle of relativity allows us to say that from the observer inside the car's point of view, he is at rest and it is the observer on the side of the road who moves. Since both observers are in inertial frames, physical experiments must always produce the same results, namely that the car's driver observes our time pass more slowly than his own. How is it possible for both frames to see the other as passing more slowly? Couldn't they stop, meet, and determine whose clock shows greater time passage? It could only be one clock or the other.
This is an example of the well known twin paradox:[Note 8]
- According to those on Earth, a twin taking a space trip at high speeds has a slower biological clock than an Earth-bound twin. The traveler therefore returns to Earth to find their stay-at-home sibling has aged in comparison. The age difference seems a paradox if one adopts the view that, to the traveler, the Earth-bound sibling appears to experience a high speed history, and so should age more slowly according to the traveler. That is, to the traveler upon return, the stay-at-home should be the younger twin, contradicting the Earth observers' expectations.
The details in resolving the paradox go beyond this article's scope. Suffice it to say that the twins are subject to relative acceleration and thus do not remain at all times in two frames that are related as inertial frames. Acceleration implies departure from an inertial frame, and Special Relativity regards only the laws of physics in inertial frames. Once forces like acceleration (or deceleration) or gravity are introduced, one must turn to the Theory of General Relativity to explain motion's effects on length and the passage of time.
The pole-in-the-barn paradox
The failure of simultaneity in special relativity is illustrated by the pole-in-the-barn paradox. The scenario includes a long, horizontal pole and a barn with both a front and a rear door, as shown in Figure 8.1. The pole's length is Lp in its rest frame, and the distance between the barn's two doors is Lb < Lp. As such, when at rest the pole cannot fit inside the barn. However, when moving at relativistic speeds, the pole can be shorter than the barn owing to length contraction and will fit inside the barn. For a complete description, see the pole-in-the-barn paradox article.
Energy and momentum
As pointed out, Newton's laws of mechanics are not compatible with the Lorentz transformation required so that Maxwell's equations keep the same form for all inertial observers, as specified by the first postulate of special relativity. [Note 3] Without going into much detail, the changes in Newton's laws are outlined here, and some of their more notable implications. The most amazing aspect of special relativity is the abandonment of absolute time, a fundamental assumption of the Newtonian theory, and special relativity's introduction of space and time as being interconnected. This aspect has been explained at length above.
These ideas mean that Newton's second law must be expressed as:
which states in words that force is the rate of change of momentum. The above form of the law is not changed (although its often-stated form that force is mass times acceleration is not equivalent), but the mass changes:
where the symbol m0 represents the rest mass of a body, that is, its mass as seen a frame of reference where it is stationary, and the symbol m is now the relativistic mass, the mass of the body seen in a frame where the mass is moving at a constant speed v.
This formula for mass can be rearranged by using the smallness of the ratio v/c to expand the square root as a series in this ratio:
The second term is the kinetic energy of the body, and Einstein interpreted the left side of this equation as the total energy of the body, resulting in the famous expression E = mc2 that expresses the ability to convert mass into energy, the mechanism underlying nuclear power generation, as well as Nuclear weapons.
It should be noted that this mass-energy equivalence is not based simply upon the above series expansion, but is inextricably mixed up with the interchangeability of space and time. All physical quantities are no longer vectors in space only, as with Newton's mechanics, but are vectors in space and time, so-called four-vectors. In particular, energy and momentum make up an energy-momentum four vector:[Note 9]
where v = {vi} is the three-vector of velocity of a particle, and with γ a symbol for:
The first three components are the space-like components and the fourth component is the time-like component. It is related to the energy, E:
References
- ↑ For example, see the discussion by Michio Kaku (2008). Physics of the impossible: a scientific exploration into the world of phasers, force fields, teleportation, and time travel. Random House Digital Inc., pp. 62 ff. ISBN 0385520697.
- ↑ Jeremy Bernstein (1997). Albert Einstein and the frontiers of physics. Oxford University Press, p. 55. ISBN 0195120299. “On the other hand, how much did Einstein know of the Michelson-Morely experiment?...At various times he said that he had either heard of Michelson's work, or that he hadn't, or that if he had heard of it, it didn't matter.”
- ↑ 3.0 3.1 Albert Einstein (1952). “The foundation of the general theory of relativity”, A Sommerfeld, ed: The Principle of Relativity: a collection of original memoirs on the special and general theory of relativity, Republication of 1923 translation by W Perret and GB Jefferey of original article. Courier Dover Publications, p. 111. ISBN 0486600815. “Special principle of relativity: If a system of coordinates K is chosen so that, in relation to it, physical laws hold good in their simplest form, the same laws hold good in relation to any other system of coordinates K' moving in uniform translation relatively to K.” Notice the emphasis upon simplest form for the laws, the key point that separates inertial frames from others.
- ↑ Albert Einstein (1952). “The foundation of the general theory of relativity”, A. Sommerfeld, editor: The Principle of Relativity: a collection of original memoirs on the special and general theory of relativity, Republication of 1923 translation by W Perret and GB Jefferey of original article. Courier Dover Publications, p. 111. ISBN 0486600815. “Thus, the special theory of relativity does not depart from classical mechanics through the postulate of relativity but through the postulate of the constancy of light in vacuo, from which, in combination with the special principle of relativity, there follow, in the well known way, the relativity of simultaneity, the Lorentzian transformation, and the related laws for the behaviour of moving bodies and clocks.”
- ↑ This example is very common in the literature of relativity. For example, see John R. Taylor (2005). “§15.4 The relativity of time; time dilation & Figure 15.3”, Classical mechanics. University Science Books, pp. 603 ff. ISBN 189138922X.
- ↑ The use of a "light clock" is introduced by RP Feynman (1963). “§15.4 Transformation of time”, The Feynman Lectures on Physics, Volume 1. Addison-Wesley, pp. 15-5 ff. and also RP Feynman (2011). “§3-4 Transformation of time”, Six not-so-easy pieces, 4th ed. Basic Books, pp. 59 ff. ISBN 0465025269. This clock is idealized in that the mechanisms for reflecting the light and detecting its arrival and departure times have not been examined, nor any implications these mechanisms might have upon actual time measurements. If one is not ready to accept the possibility of a viable light clock, an old fashioned pendulum clock can be substituted that swings back and forth in the plane perpendicular to the direction of motion. The argument remains the same.
- ↑
The algebra here is as follows. Note the identity:
- ↑ The twin paradox has been studied experimentally by putting clocks on airplanes and comparing them with Earth-bound clocks. The faster traveling clocks develop a time lag. See Don Bernett Lichtenberg (2007). “§10.3 The twin paradox”, The universe and the atom. Springer, pp. 116 ff. ISBN 9812705619. A theoretical analysis is provided by Vesselin Petkov (2007). Relativity and the Nature of Spacetime, 2nd ed. Springer, pp. 146 ff. ISBN 3642019528.
- ↑ For a discussion see, for example, Richard Kent Cooper, Claudio Pellegrini (1999). “§9.6 Energy-momentum four-vector”, Modern analytic mechanics. Springer, p. 227. ISBN 0306459582.
- ↑ "Perhaps, too, we shall have to construct an entirely new mechanics that we only succeed in catching a glimpse of, where, inertia increasing with the velocity, the velocity of light would become an impassable limit. The ordinary mechanics, more simple, would remain a first approximation, since it would be true for velocities not too great, so that the old dynamics would still be found under the new." - https://en.wikisource.org/wiki/The_Principles_of_Mathematical_Physics#Future_Mathematical_Physics.