Complex number/Citable Version: Difference between revisions
imported>Aleksander Stos m (→Integration: minor formatting) |
Pat Palmer (talk | contribs) mNo edit summary |
||
| (132 intermediate revisions by 14 users not shown) | |||
| Line 1: | Line 1: | ||
{{subpages}} | |||
'''Complex numbers''' are numbers of the form <math>a+bi</math>, where <math>a</math> and <math>b</math> are [[real number]]s and <math>i</math> denotes a number satisfying <math>i^2=-1</math>.<ref>This article follows the usual convention in [[mathematics]] and [[physics]] of using <math>i</math> as the imaginary unit. Complex numbers are frequently used in [[electrical engineering]], but in that discipline it is usual to use <math>j</math> instead, reserving <math>i</math> for [[electrical current]]. This usage is found in some [[programming language]]s too, notably [[Python]].</ref> Of course, since the square of any real number is nonnegative, <math>i</math> cannot be a real number. At first glance, it is not even clear whether such an object exists and can be reasonably called a number; for example, can we sensibly associate with <math>i</math> natural operations such as addition and multiplication? As it happens, we can define mathematical operations for these "complex numbers" in a consistent and sensible way and, perhaps more importantly, using complex numbers provides mathematicians, physicists, and engineers with an extremely powerful approach to expressing parts of these sciences in a convenient and natural-feeling way. | |||
==Historical example == | |||
The need for complex numbers might have appeared for the first time during the sixteenth century, when Italian mathematicians like [[Scipione del Ferro]], [[Niccolò Fontana Tartaglia]], [[Gerolamo Cardano]] and [[Rafael Bombelli]] tried to solve [[cubic equation|cubic equations]]. Even for equations with three [[real number|real]] solutions, the method they used sometimes required calculations with numbers whose squares are negative. Here is such an example (with modern notation). Let us consider the equation | |||
:<math>4 | : <math>x^3=15x+4. \ </math> | ||
[[Cardano's method]] for solving it suggests looking for a solution by writing it as a sum <math>x=u+v</math>, where another condition on <math>u</math> and <math>v</math> is to be decided later. Recording this in the equation, we have, once the left member is expanded, | |||
:<math> | : <math>u^3+3u^2v+3uv^2+v^3=15(u+v)+4, \ </math> | ||
which can be written as | |||
= | : <math>u^3+(3uv-15)(u+v)+v^3=4. \ </math> | ||
Now we recall that we did not completely specify <math>u</math> and <math>v</math>; we only required that <math>x=u+v</math>. Hence, we can choose another condition on <math>u</math> and <math>v</math>. We pick this condition to be <math>3uv-15=0</math>, or <math>uv=5</math>, in order to simplify the above equation. This implies that <math>u^3</math> and <math>v^3</math> are numbers whose sum and product are given by | |||
: <math>\begin{cases} | |||
u^3v^3=125, \\ | |||
u^3+v^3=4. | |||
\end{cases}</math> | |||
It follows from the second equation that <math>v^3 = 4 - u^3</math>. Substituting this in the first equation, we get <math>u^3 (4-u^3) = 125</math>. Hence we may find some values for <math>u^3</math> by solving the equation <math>x(4-x) = 125</math>. Get rid of the brackets and move the number 125 to the left-hand side to get the [[quadratic equation]] | |||
= | : <math>x^2-4x+125=0. \ </math> | ||
=== | Its [[discriminant]] is <math>\Delta=(-4)^2-4\cdot 125=-484=-22^2</math>, which is ''negative'', so that the quadratic equation has ''no real solution'': the usual formulae giving the solutions require taking the [[square root]] of the discriminant, which is undefined here. | ||
Well, let us be bold and write <math>\Delta=\left(22\sqrt{-1}\right)^2</math>. Here, the symbol <math>\sqrt{-1}</math> denotes an hypothetical number whose square would be <math>-1.</math> At this stage, such a number has no meaning (squares of real numbers are always nonnegative), but we use it in a purely formal way. Using this symbol, we can write the "solutions" to the quadratic equation as | |||
:<math> | : <math>u^3=\frac{4+22\sqrt{-1}}{2}=2+11\sqrt{-1}</math> and <math>v^3=\frac{4-22\sqrt{-1}}{2}=2-11\sqrt{-1}.</math> | ||
It remains to find cube roots of these "numbers". A straightforward calculation shows that <math>u=2+\sqrt{-1}</math> and <math>v=2-\sqrt{-1}</math> do the job. For instance, remembering the rule <math>\left(\sqrt{-1}\right)^2=-1</math>, we have | |||
:<math>( | : <math>\left(2+\sqrt{-1}\right)^3=2^3+3\cdot 2^2\sqrt{-1}+3\cdot 2\left(\sqrt{-1}\right)^2+\left(\sqrt{-1}\right)^3</math> | ||
::::: <math>=8+12\sqrt{-1}-6-\sqrt{-1}=2+11\sqrt{-1}.</math> | |||
But now, going back to the original cubic equation, we get the ''real'' solution <math>x=u+v=(2+\sqrt{-1})+(2-\sqrt{-1})=4</math>. One can verify it is indeed a solution, as <math>4^3=64=15\cdot 4+4</math>. And once this solution is found, it is easy to find the two other solutions <math>-2\pm\sqrt3</math>, which are also real. | |||
The fact that the formal calculations managed to give a real solution suggests that the "number" <math>\sqrt{-1}</math> may have some sense. But to really give it a legitimate status, one has to construct a new set of numbers, containing the real numbers, but also other numbers whose squares may be negative real numbers. This will be the set of ''complex numbers''. A rigorous construction of this set as pairs of real numbers was given much later by [[William Rowan Hamilton]] in 1837; this construction is explained [[Complex number#Formal definition|later in this article]]. | |||
==Working with complex numbers== | |||
As a first step in giving some legitimacy to the "number" <math>\sqrt{-1}</math>, we will explain how to compute with it. How do you add, multiply and divide expressions with this number? It turns out that this is not that difficult; the main rule to keep in mind is that the square of <math>\sqrt{-1}</math> equals <math>-1</math>. | |||
In the remainder of the article, we will use the letter <math>i</math> to denote one solution of the equation <math>i^2 = -1</math>, where we previously used <math>\sqrt{-1}</math>.<ref>Part of the reason for not using <math>\sqrt{-1}</math> is that the symbol <math>\sqrt{a}</math> (or <math>\sqrt[n]{a}</math>) with <math>a\in\mathbb{C}</math> is sometimes used to denote the set of ''complex roots'' of <math>a</math>, i.e., the set of the solutions of the equation <math>x^2=a</math> (<math>x^n=a</math> respectively). The set contains 2 (<math>n</math>, respectively) "equally important" elements and there is no canonical way to distinguish a "representative". Consequently, no computations are performed using this symbol.</ref> With this convention, all complex numbers can be written as <math>a + bi</math>, where <math>a</math> and <math>b</math> are '''real''' numbers. We call <math>a</math> the real part of the complex number and <math>b</math> the imaginary part. Complex numbers whose imaginary part is <math>0</math> are of the form <math>a+0i</math>. In this way, the real number <math>a</math> is considered as the complex number <math>a + 0i</math> whose imaginary part is zero. | |||
===Basic operations=== | |||
Addition of complex numbers is straightforward, <math>(a + bi) + (c + di) = (a + c) + (b + d)i.</math> The result is again a complex number. | |||
:<math> | Multiplication is more interesting. Suppose we want to compute <math>(a+bi)(c+di)</math>. Using <math>i^2 = -1</math>, we can rewrite this product in a form which clearly shows it to be another complex number: | ||
:<math>(a + bi)(c + di) = ac + adi + bci + bdi^2 = (ac - bd) + (bc + ad)i. \ </math> | |||
To handle division, we simply note that <math>(c + di)(c - di) = c^2 +d^2</math>, so | |||
:<math>\frac{1}{c + di} = \frac{c - di}{c^2 + d^2}, </math> | |||
from which it follows that | |||
:<math>\frac{a + bi}{c + di} = \frac{(ac + bd) + (bc - ad)i}{c^2 + d^2}.</math> | |||
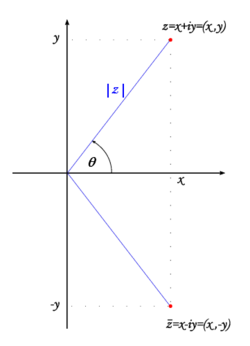
Going a bit further, we can introduce the important operation of complex conjugation. Given an arbitrary complex number <math>z = x + iy</math>, we define its complex conjugate to be <math>\bar{z} = x - iy</math>. Using the identity <math>(a + b)(a - b) = a^2 - b^2</math> we derive the important formula | |||
:<math>z \bar{z} = x^2 + y^2</math> | |||
and we define the modulus of a complex number z to be | |||
:<math>|z| = \sqrt{z \bar{z}}</math> | |||
Note that the modulus of a complex number is always a ''nonnegative real'' number. | |||
The modulus (also called absolute value) satisfies three important properties that are completely analogous to the properties of the absolute value of real numbers | The modulus (also called absolute value) satisfies three important properties that are completely analogous to the properties of the absolute value of real numbers | ||
*<math>|z| \ge 0</math>; furthermore, <math>|z| = 0</math> if and only if <math>z = 0</math> | |||
*<math>|z_1 z_2| = |z_1| |z_2| \ </math> | |||
*<math>|z_1 + z_2 | \le |z_1| + |z_2|</math> | |||
The last inequality is known as the [[triangle inequality]]. | The last inequality is known as the [[triangle inequality]]. | ||
===The | ===The complex exponential=== | ||
Recall that in real analysis, the ordinary [[exponential]] function may be defined as | Recall that in real analysis, the ordinary [[exponential]] function may be defined as | ||
:<math> | :<math>e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots</math> | ||
The same series may be used to define the ''complex'' exponential function | The same series may be used to define the ''complex'' exponential function | ||
:<math> | :<math>e^z = 1 + z + \frac{z^2}{2!} + \frac{z^3}{3!} + \cdots</math> | ||
(where, of course, convergence is defined in terms of the complex modulus, instead of the real absolute value). | (where, of course, convergence is defined in terms of the complex modulus, instead of the real absolute value). | ||
The complex exponential has the same multiplicative property that holds for real numbers, namely | |||
The complex exponential has the same multiplicative property that holds for real numbers,namely | |||
:<math>e^{z_1 z_2} = e^{z_1} e^{z_2} \ </math> | :<math>e^{z_1 + z_2} = e^{z_1} e^{z_2} \ </math> | ||
The complex exponential function has the important property that | The complex exponential function has the important property that | ||
| Line 101: | Line 91: | ||
:<math>e^{i\theta} = \cos \theta + i \sin \theta \ </math> | :<math>e^{i\theta} = \cos \theta + i \sin \theta \ </math> | ||
as may be seen immediately by substituting <math>z = i\theta</math> and comparing terms with the usual power series expansions of <math>\sin \theta</math> and <math>\cos \theta</math>. | as may be seen immediately by substituting <math>z = i\theta</math> and comparing terms with the usual [[Taylor series|power series expansions]] of <math>\sin \theta</math> and <math>\cos \theta</math>. | ||
The familiar [[ | The familiar [[trigonometric function|trigonometric]] identity | ||
:<math>\sin^2 \theta + \cos^2 \theta = 1 \ </math> | :<math>\sin^2 \theta + \cos^2 \theta = 1 \ </math> | ||
| Line 109: | Line 99: | ||
immediately implies the important formula | immediately implies the important formula | ||
:<math>|e^{i\theta}| = 1</math>, for any <math>\theta \in \mathbb{R} | :<math>|e^{i\theta}| = 1</math>, for any <math>\theta \in \mathbb{R}.</math> | ||
so | Of course, there is no reason to assume this identity. We only need note that <math>\overline{e^{i\theta}} = e^{-i\theta}</math>, so | ||
:<math>|e^{i\theta}|^2 = e^{i\theta}e^{-i\theta} = e^0 = 1 \ </math> | :<math>|e^{i\theta}|^2 = e^{i\theta}e^{-i\theta} = e^0 = 1. \ </math> | ||
==Geometric | ===Geometric interpretation=== | ||
Since a complex number <math>z = x + iy</math> | [[Image:Complex_plane3.png|thumb|right|250px|Graphical representation of a complex number and its conjugate]] | ||
Since a complex number <math>z = x + iy</math> is specified by two real numbers, namely <math>x</math> and <math>y</math>, it can be interpreted as the point <math>(x,y)</math> in the plane. When complex numbers are represented as points in the plane, the resulting diagrams are known as [[Robert Argand|Argand]] diagrams, after [[Robert Argand]]. The geometric representation of complex numbers turns out to be very useful, both as an aid to understanding the properties of complex numbers and as a tool in applying complex numbers to [[geometry|geometrical]] and [[physics|physical]] problems. | |||
There are no real surprises when we look at addition and subtraction in isolation: addition of complex numbers is not essentially different from addition of [[vector]]s in <math>\mathbb{R}^2</math>. Similarly, if <math>\alpha \in \mathbb{R}</math> is real, multiplication by <math>\alpha</math> is just scalar multiplication. In <math>\mathbb{C}</math> we have | There are no real surprises when we look at addition and subtraction in isolation: addition of complex numbers is not essentially different from addition of [[vector]]s in <math>\mathbb{R}^2</math>. Similarly, if <math>\alpha \in \mathbb{R}</math> is real, multiplication by <math>\alpha</math> is just scalar multiplication. In <math>\mathbb{C}</math> we have | ||
:<math>z_1 + z_2 = (x_1 + iy_1) + (x_2 + iy_2) = (x_1 + x_2) + i(y_1 + y_2) \ </math> | :<math>z_1 + z_2 = (x_1 + iy_1) + (x_2 + iy_2) = (x_1 + x_2) + i(y_1 + y_2) \ </math> | ||
| Line 128: | Line 116: | ||
and | and | ||
:<math>\alpha z = \alpha(x + iy) = \alpha x + i\alpha y \ </math> | :<math>\alpha z = \alpha(x + iy) = \alpha x + i\alpha y. \, </math> | ||
To put it | To put it succinctly, <math>\mathbb{C}</math> is a 2-dimensional [[real number|real]] [[vector space]] with respect to the usual operations of addition of complex numbers and multiplication by a real number. There doesn't seem to be much more to say. But there ''is'' more to say, and that is that the multiplication of ''complex'' numbers has geometric significance. This is most easily seen if we take advantage of the complex exponential, and write complex numbers in [[polar coordinates|polar]] form | ||
:<math>z = r e^{i\theta}</math> | :<math>z = r e^{i\theta}.</math> | ||
Here, r is simply the modulus <math>\sqrt{x^2 + y^2}</math> or vector length. The number <math>\theta</math> is just the angle formed with the | Here, r is simply the modulus <math>|z| = \sqrt{x^2 + y^2}</math> or vector length. The number <math>\theta</math> is just the angle formed with the <math>x</math>-axis, and is called the ''argument''. Now, when complex numbers are written in polar form, multiplication is very interesting | ||
:<math>z_1 z_2 = (r_1 e^{i\theta_1}) (r_2 e^{i\theta_2}) = r_1 r_2 e^{i(\theta_1 + \theta_2)}</math> | :<math>z_1 z_2 = (r_1 e^{i\theta_1}) (r_2 e^{i\theta_2}) = r_1 r_2 e^{i(\theta_1 + \theta_2)}.</math> | ||
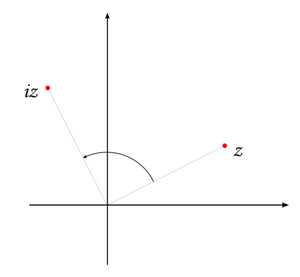
[[Image:Graphical_multiplication1.png|thumb|300px|left|Multiplication by <math>i</math> amounts to rotation by 90 degrees]] | |||
In other words, multiplication by a complex number <math>z</math> has the effect of simultaneously scaling by the number's modulus and ''rotating'' by its argument. This is really astounding. For example, to multiply a given complex number <math>z</math> by <math>i</math> we need only to rotate <math>z</math> by <math>\pi/2</math> (that is, 90 degrees). [[Translation (geometry)|Translation]] corresponds to complex addition, [[scale|scaling]] to multiplication by a real number, and [[rotation]] to multiplication by a complex number of unit modulus. The one type of [[coordinate transformation]] that is missing from this list is [[reflection]]. On the other hand, there is an arithmetic operation we have not considered, and that is division. Recall that | |||
:<math>\frac{1}{z} = \frac{\bar{z}}{|z|^2}.</math> | |||
In other words, up to a scaling factor, division of one by <math>z</math> is just complex conjugation. Returning to the representation of complex numbers in rectangular form, we note that complex conjugation is just the transformation (or map) <math>x + iy \;\mapsto\; x - iy</math> or, in vector notation, <math>(x, y)\; \mapsto \;(x, -y)</math>. This is nothing other than reflection in the <math>x</math>-axis, and any other reflection may be obtained by combining that transformation with rotations and translations. | |||
In other words, up to a scaling factor, division by | |||
Historically, this observation was very important and led to the search for higher dimensional algebras that could "arithmetize" [[Euclidean geometry]]. It turns out that there are such generalizations in dimensions 4 and 8, known as the [[quaternions]] and [[octonions]] (also known as [[Cayley numbers]]). At that point, the process stops, but the ideas developed in this process have played an important role in the development of modern [[differential geometry]] and [[physics|mathematical physics]]). | Historically, this observation was very important and led to the search for higher dimensional algebras that could "arithmetize" [[Euclidean geometry]]. It turns out that there are such generalizations in dimensions 4 and 8, known as the [[quaternions]] and [[octonions]] (also known as [[Cayley numbers]]). At that point, the process stops, but the ideas developed in this process have played an important role in the development of modern [[differential geometry]] and [[physics|mathematical physics]]). | ||
== | ==Algebraic closure== | ||
An important property of the set of complex numbers is that it is [[algebraically closed]]. This means that any non-constant [[polynomial]] with complex coefficients has a complex root. This result is known as the [[Fundamental Theorem of Algebra]]. | |||
This is actually quite remarkable. We started out with the real numbers. There are many polynomials with real coefficients that do not have a real root. We took just one of these, the polynomial <math>x^2+1</math>, and we introduced a new number, <math>i</math>, which is defined to be a root of the polynomial. Suddenly, all non-constant polynomials have a root in this new setting where we allow complex numbers. | |||
There are many proofs of the Fundamental Theorem of Algebra. Many of the simplest depend crucially on [[complex analysis]]. But it is by no means necessary to rely on complex analysis here. A proof using [[field theory]] is alluded to at the very end of this article. | |||
==Complex numbers in physics== | |||
: | Complex numbers appear everywhere in mathematical physics, but one area where the role of complex numbers is especially difficult to ignore is in [[quantum mechanics]]. There are a number of ways of formulating the basic laws of quantum mechanics, but here we consider just one: the [[Schrödinger equation]], discovered by Erwin Schrödinger in 1926. In rectangular coordinates, it may be written | ||
:<math>i\hbar \frac{\partial \psi}{\partial t} = - \frac{\hbar^2}{2m}\Delta\psi + V(x,y,z)\psi,</math> | |||
where | |||
:<math>\Delta = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2}</math> | |||
is known as the [[Laplacian operator]] and <math>V(x,y,z)</math> is the potential function. (As a practical example, minus the gradient of the potential function might represent the attractive force between the nucleus of a hydrogen atom and an electron). | |||
==Formal definition== | |||
This | This all shows that complex numbers behave very much like real numbers and that they can be very useful, but it does not prove that they exist. In fact, it is quite easy to go wrong when using complex numbers. Consider for instance the following computation: | ||
:<math>-1=\sqrt{-1}\times\sqrt{-1}=\sqrt{(-1)\times(-1)}=\sqrt{1}=1.</math> | |||
This computation seems to show that <math>-1</math> equals <math>1</math>, which is nonsense. The point is that the second equality can not be applied. Positive real numbers satisfy the identity | |||
:<math> \sqrt{a}\times\sqrt{b} = \sqrt{a \times b}, </math> | |||
but this identity does not hold for negative real numbers, whose square roots are not real. | |||
This | One possibility to feel more secure when using complex numbers is to define them in terms of constructs which are better understood. This approach was taken by [[William Rowan Hamilton|Hamilton]], who defined complex numbers as [[ordered pair|ordered pairs]] of real numbers, that is, | ||
:<math>\mathbb{C}= \{ (a,b) \colon a,b\in \mathbb{R} \}.</math> | |||
Such pairs can be added and multiplied as follows | |||
*addition: <math>(a, b) + (c, d) = (a + c, b + d)</math> | |||
*multiplication: <math>(a, b)(c, d) = (ac - bd, bc + ad)</math> | |||
The multiplication may look artificial, but it is inspired by the formula | |||
:<math>(a + bi)(c + di) = (ac - bd) + (bc + ad)i. \ </math> | |||
which we derived before. | |||
These definitions satisfy most of the basic properties of addition and multiplication of real numbers, and we can employ many formulas from the elementary algebra we are accustomed to. More specifically, the sum (or the product) of two numbers does not depend on the order of terms;<ref>that is, the addition (multiplication) is [[commutativity|commutative]]</ref> the sum (product) of three or more elements does not depend on order of operations ('we can suppress the parentheses');<ref>This is called [[associativity]]</ref> the product of a complex number with a sum of two other numbers expands in the usual way.<ref>In other words, multiplication is [[distributivity|distributive]] over addition</ref> In mathematical language this means that with addition and multiplication defined this way, <math>\mathbb{C}</math> satisfies the [[axiom|axioms]] for a [[field]] and is called the field of complex numbers. | |||
Now we are ready to understand the 'real' meaning of <math>i</math>. Observe that the pairs of type (<math>a</math>,0) are identical<ref>i.e., [[isomorphism|isomorphic]], which basically means that the mapping <math> \mathbb{C}\ni (a,0)\mapsto a\in\mathbb{R},</math> preserves the addition and multiplication.</ref> to the set of reals, so we write <math>(a,0)=a</math>. Observe also that by definition <math>(0,1)(0,1) = (-1,0)=-1</math>. In other words, we can define <math>i</math>, the number satisfying <math>i^2=-1</math>, as the pair (0,1).<ref>although we should be careful about giving this particular definition too much credit: after all, the number <math>(0,-1)</math> has exactly the same property!</ref> | |||
Another way to define the complex numbers comes from [[field theory]]. Because <math>x^2+1</math> is [[irreducible polynomial|irreducible]] in the [[polynomial ring]] <math>\mathbb{R}[x]</math>, the [[ideal (ring theory)|ideal]] generated by <math>x^2+1</math> is a [[maximal ideal]].<ref>An ideal <math>I = \left(f(x)\right)</math> in a polynomial ring over a field is maximal if and only if <math>f(x)</math> is irreducible over the field.</ref> Therefore, the [[quotient ring]] <math> \mathbb{C}=\mathbb{R}[x]/\left(x^2+1\right)</math> is a [[field (mathematics)|field]]. We can choose the polynomials of degree at most 1 as the representatives for the equivalence classes in this quotient ring. So in a sense, we can imagine that the dummy variable <math>x</math> is the imaginary number <math>i</math>, and the elements of the quotient ring behave exactly the way we expect the complex numbers to behave. For example, <math>x^2</math> is in the same equivalence class as <math>-1</math>, and so <math>x^2=-1</math> in this quotient ring. (As a final comment in this analysis, we could next show that <math>\mathbb{C}</math> has no finite [[field extension|extension]] and must therefore be [[algebraic closure|algebraically closed]].) | |||
| | |||
| | |||
==Notes and references== | ==Notes and references== | ||
{{reflist}} | {{reflist|2}} | ||
Latest revision as of 09:07, 16 December 2024
Complex numbers are numbers of the form , where and are real numbers and denotes a number satisfying .[1] Of course, since the square of any real number is nonnegative, cannot be a real number. At first glance, it is not even clear whether such an object exists and can be reasonably called a number; for example, can we sensibly associate with natural operations such as addition and multiplication? As it happens, we can define mathematical operations for these "complex numbers" in a consistent and sensible way and, perhaps more importantly, using complex numbers provides mathematicians, physicists, and engineers with an extremely powerful approach to expressing parts of these sciences in a convenient and natural-feeling way.
Historical example
The need for complex numbers might have appeared for the first time during the sixteenth century, when Italian mathematicians like Scipione del Ferro, Niccolò Fontana Tartaglia, Gerolamo Cardano and Rafael Bombelli tried to solve cubic equations. Even for equations with three real solutions, the method they used sometimes required calculations with numbers whose squares are negative. Here is such an example (with modern notation). Let us consider the equation
Cardano's method for solving it suggests looking for a solution by writing it as a sum , where another condition on and is to be decided later. Recording this in the equation, we have, once the left member is expanded,
which can be written as
Now we recall that we did not completely specify and ; we only required that . Hence, we can choose another condition on and . We pick this condition to be , or , in order to simplify the above equation. This implies that and are numbers whose sum and product are given by
It follows from the second equation that . Substituting this in the first equation, we get . Hence we may find some values for by solving the equation . Get rid of the brackets and move the number 125 to the left-hand side to get the quadratic equation
Its discriminant is , which is negative, so that the quadratic equation has no real solution: the usual formulae giving the solutions require taking the square root of the discriminant, which is undefined here.
Well, let us be bold and write . Here, the symbol denotes an hypothetical number whose square would be At this stage, such a number has no meaning (squares of real numbers are always nonnegative), but we use it in a purely formal way. Using this symbol, we can write the "solutions" to the quadratic equation as
- and
It remains to find cube roots of these "numbers". A straightforward calculation shows that and do the job. For instance, remembering the rule , we have
But now, going back to the original cubic equation, we get the real solution . One can verify it is indeed a solution, as . And once this solution is found, it is easy to find the two other solutions , which are also real.
The fact that the formal calculations managed to give a real solution suggests that the "number" may have some sense. But to really give it a legitimate status, one has to construct a new set of numbers, containing the real numbers, but also other numbers whose squares may be negative real numbers. This will be the set of complex numbers. A rigorous construction of this set as pairs of real numbers was given much later by William Rowan Hamilton in 1837; this construction is explained later in this article.
Working with complex numbers
As a first step in giving some legitimacy to the "number" , we will explain how to compute with it. How do you add, multiply and divide expressions with this number? It turns out that this is not that difficult; the main rule to keep in mind is that the square of equals .
In the remainder of the article, we will use the letter to denote one solution of the equation , where we previously used .[2] With this convention, all complex numbers can be written as , where and are real numbers. We call the real part of the complex number and the imaginary part. Complex numbers whose imaginary part is are of the form . In this way, the real number is considered as the complex number whose imaginary part is zero.
Basic operations
Addition of complex numbers is straightforward, The result is again a complex number.
Multiplication is more interesting. Suppose we want to compute . Using , we can rewrite this product in a form which clearly shows it to be another complex number:
To handle division, we simply note that , so
from which it follows that
Going a bit further, we can introduce the important operation of complex conjugation. Given an arbitrary complex number , we define its complex conjugate to be . Using the identity we derive the important formula
and we define the modulus of a complex number z to be
Note that the modulus of a complex number is always a nonnegative real number. The modulus (also called absolute value) satisfies three important properties that are completely analogous to the properties of the absolute value of real numbers
- ; furthermore, if and only if
The last inequality is known as the triangle inequality.
The complex exponential
Recall that in real analysis, the ordinary exponential function may be defined as
The same series may be used to define the complex exponential function
(where, of course, convergence is defined in terms of the complex modulus, instead of the real absolute value).
The complex exponential has the same multiplicative property that holds for real numbers, namely
The complex exponential function has the important property that
as may be seen immediately by substituting and comparing terms with the usual power series expansions of and .
The familiar trigonometric identity
immediately implies the important formula
- , for any
Of course, there is no reason to assume this identity. We only need note that , so
Geometric interpretation
Since a complex number is specified by two real numbers, namely and , it can be interpreted as the point in the plane. When complex numbers are represented as points in the plane, the resulting diagrams are known as Argand diagrams, after Robert Argand. The geometric representation of complex numbers turns out to be very useful, both as an aid to understanding the properties of complex numbers and as a tool in applying complex numbers to geometrical and physical problems.
There are no real surprises when we look at addition and subtraction in isolation: addition of complex numbers is not essentially different from addition of vectors in . Similarly, if is real, multiplication by is just scalar multiplication. In we have
and
To put it succinctly, is a 2-dimensional real vector space with respect to the usual operations of addition of complex numbers and multiplication by a real number. There doesn't seem to be much more to say. But there is more to say, and that is that the multiplication of complex numbers has geometric significance. This is most easily seen if we take advantage of the complex exponential, and write complex numbers in polar form
Here, r is simply the modulus or vector length. The number is just the angle formed with the -axis, and is called the argument. Now, when complex numbers are written in polar form, multiplication is very interesting
In other words, multiplication by a complex number has the effect of simultaneously scaling by the number's modulus and rotating by its argument. This is really astounding. For example, to multiply a given complex number by we need only to rotate by (that is, 90 degrees). Translation corresponds to complex addition, scaling to multiplication by a real number, and rotation to multiplication by a complex number of unit modulus. The one type of coordinate transformation that is missing from this list is reflection. On the other hand, there is an arithmetic operation we have not considered, and that is division. Recall that
In other words, up to a scaling factor, division of one by is just complex conjugation. Returning to the representation of complex numbers in rectangular form, we note that complex conjugation is just the transformation (or map) or, in vector notation, . This is nothing other than reflection in the -axis, and any other reflection may be obtained by combining that transformation with rotations and translations.
Historically, this observation was very important and led to the search for higher dimensional algebras that could "arithmetize" Euclidean geometry. It turns out that there are such generalizations in dimensions 4 and 8, known as the quaternions and octonions (also known as Cayley numbers). At that point, the process stops, but the ideas developed in this process have played an important role in the development of modern differential geometry and mathematical physics).
Algebraic closure
An important property of the set of complex numbers is that it is algebraically closed. This means that any non-constant polynomial with complex coefficients has a complex root. This result is known as the Fundamental Theorem of Algebra.
This is actually quite remarkable. We started out with the real numbers. There are many polynomials with real coefficients that do not have a real root. We took just one of these, the polynomial , and we introduced a new number, , which is defined to be a root of the polynomial. Suddenly, all non-constant polynomials have a root in this new setting where we allow complex numbers.
There are many proofs of the Fundamental Theorem of Algebra. Many of the simplest depend crucially on complex analysis. But it is by no means necessary to rely on complex analysis here. A proof using field theory is alluded to at the very end of this article.
Complex numbers in physics
Complex numbers appear everywhere in mathematical physics, but one area where the role of complex numbers is especially difficult to ignore is in quantum mechanics. There are a number of ways of formulating the basic laws of quantum mechanics, but here we consider just one: the Schrödinger equation, discovered by Erwin Schrödinger in 1926. In rectangular coordinates, it may be written
where
is known as the Laplacian operator and is the potential function. (As a practical example, minus the gradient of the potential function might represent the attractive force between the nucleus of a hydrogen atom and an electron).
Formal definition
This all shows that complex numbers behave very much like real numbers and that they can be very useful, but it does not prove that they exist. In fact, it is quite easy to go wrong when using complex numbers. Consider for instance the following computation:
This computation seems to show that equals , which is nonsense. The point is that the second equality can not be applied. Positive real numbers satisfy the identity
but this identity does not hold for negative real numbers, whose square roots are not real.
One possibility to feel more secure when using complex numbers is to define them in terms of constructs which are better understood. This approach was taken by Hamilton, who defined complex numbers as ordered pairs of real numbers, that is,
Such pairs can be added and multiplied as follows
- addition:
- multiplication:
The multiplication may look artificial, but it is inspired by the formula
which we derived before.
These definitions satisfy most of the basic properties of addition and multiplication of real numbers, and we can employ many formulas from the elementary algebra we are accustomed to. More specifically, the sum (or the product) of two numbers does not depend on the order of terms;[3] the sum (product) of three or more elements does not depend on order of operations ('we can suppress the parentheses');[4] the product of a complex number with a sum of two other numbers expands in the usual way.[5] In mathematical language this means that with addition and multiplication defined this way, satisfies the axioms for a field and is called the field of complex numbers.
Now we are ready to understand the 'real' meaning of . Observe that the pairs of type (,0) are identical[6] to the set of reals, so we write . Observe also that by definition . In other words, we can define , the number satisfying , as the pair (0,1).[7]
Another way to define the complex numbers comes from field theory. Because is irreducible in the polynomial ring , the ideal generated by is a maximal ideal.[8] Therefore, the quotient ring is a field. We can choose the polynomials of degree at most 1 as the representatives for the equivalence classes in this quotient ring. So in a sense, we can imagine that the dummy variable is the imaginary number , and the elements of the quotient ring behave exactly the way we expect the complex numbers to behave. For example, is in the same equivalence class as , and so in this quotient ring. (As a final comment in this analysis, we could next show that has no finite extension and must therefore be algebraically closed.)
Notes and references
- ↑ This article follows the usual convention in mathematics and physics of using as the imaginary unit. Complex numbers are frequently used in electrical engineering, but in that discipline it is usual to use instead, reserving for electrical current. This usage is found in some programming languages too, notably Python.
- ↑ Part of the reason for not using is that the symbol (or ) with is sometimes used to denote the set of complex roots of , i.e., the set of the solutions of the equation ( respectively). The set contains 2 (, respectively) "equally important" elements and there is no canonical way to distinguish a "representative". Consequently, no computations are performed using this symbol.
- ↑ that is, the addition (multiplication) is commutative
- ↑ This is called associativity
- ↑ In other words, multiplication is distributive over addition
- ↑ i.e., isomorphic, which basically means that the mapping preserves the addition and multiplication.
- ↑ although we should be careful about giving this particular definition too much credit: after all, the number has exactly the same property!
- ↑ An ideal in a polynomial ring over a field is maximal if and only if is irreducible over the field.
































































































![{\displaystyle \mathbb {R} [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/453d1013f9dd290be70d5fe534e0d3311b0a7c6a)
![{\displaystyle \mathbb {C} =\mathbb {R} [x]/\left(x^{2}+1\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c96b0c2677d816e10cd7902c1ee99ad8ce997479)




![{\displaystyle {\sqrt[{n}]{a}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7873203eb76042fcd24056c553de8c86054a2df)







