Riemann-Hurwitz formula: Difference between revisions

From Citizendium
Jump to navigation Jump to search
imported>William Hart
mNo edit summary
mNo edit summary
 
(5 intermediate revisions by 3 users not shown)
Line 1: Line 1:
In [[algebraic geometry]] the Riemann-Hurwitz formula states that if C,D are smooth [[algebraic curves]], and <math>f:C\to D</math> is a [[finite map]] of [[degree]] <math>d</math> then the number of [[branch points]] of <math>f</math>, denoted by <math>B</math>, is given by
{{subpages}}


<math>2 (\mbox{genus}(C)-1)=2d(\mbox{genus}(D)-1)+B</math>.
In [[algebraic geometry]] the '''Riemann-Hurwitz formula''', named after [[Bernhard Riemann]] and [[Adolf Hurwitz]], states that if ''C'', ''D'' are smooth [[algebraic curve]]s, and <math>\scriptstyle f:C\to D</math> is a [[finite map]] of [[degree]] ''d'' then the number of [[branch points]] of ''f'', denoted by ''B'', is given by


Over a [[field]] in general [[characteristic]], this theorem is a consequence of the [[Riemann-Roch theorem]]. Over the [[complex numbers]], the theorem can be proved by choosing a [[triangulation]] of the curve <math>D</math> such that all the branch points of the map are nodes of the triangulation. One then considers the [[pullback]] of the triangulation to the curve <math>C</math> and computes the [[Euler characteristics]] of both curves.
: <math>2 (\mbox{genus}(C)-1)=2d(\mbox{genus}(D)-1)+B. \, </math>


[[Category:Mathematics Workgroup]]
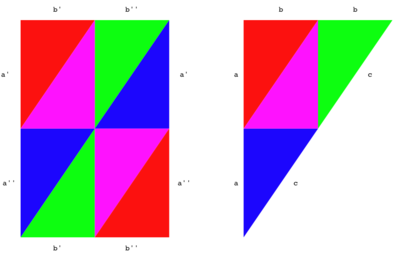
[[Image:Gludiag.png|400px|thumb|a triangulated gluing diagram for the Riemann sphere, and its pullback to a torus double cover, which is ramified over the vertices of the triangulation]]Over a [[field (algebra)|field]] in general [[Euler characteristic|characteristic]], this theorem is a consequence of the [[Riemann-Roch theorem]]. Over the [[complex numbers]], the theorem can be proved by choosing a [[triangulation]] of the curve ''D'' such that all the branch points of the map are nodes of the triangulation. One then considers the [[pullback]] of the triangulation to the curve ''C'' and computes the [[Euler characteristic]]s of both curves.[[Category:Suggestion Bot Tag]]
[[Category:CZ Live]]

Latest revision as of 11:00, 12 October 2024

This article is developing and not approved.
 Main Article
 Discussion
Related Articles  [?]
Bibliography  [?]
External Links  [?]
Citable Version  [?]
 
https://en.citizendium.org/wiki/index.php?title=Riemann-Hurwitz_formula&printable=yes
This editable Main Article is under development and subject to a disclaimer.

In algebraic geometry the Riemann-Hurwitz formula, named after Bernhard Riemann and Adolf Hurwitz, states that if C, D are smooth algebraic curves, and is a finite map of degree d then the number of branch points of f, denoted by B, is given by

a triangulated gluing diagram for the Riemann sphere, and its pullback to a torus double cover, which is ramified over the vertices of the triangulation

Over a field in general characteristic, this theorem is a consequence of the Riemann-Roch theorem. Over the complex numbers, the theorem can be proved by choosing a triangulation of the curve D such that all the branch points of the map are nodes of the triangulation. One then considers the pullback of the triangulation to the curve C and computes the Euler characteristics of both curves.

Retrieved from "https://citizendium.org/wiki/index.php?title=Riemann-Hurwitz_formula&oldid=987022"