Euler angles: Difference between revisions
imported>Paul Wormer No edit summary |
imported>Paul Wormer |
||
| Line 10: | Line 10: | ||
Euler angles are used in many different branches of physics and engineering. The present article is written from the point of view of molecular physics, where the objects to be rotated are [[molecules]]. | Euler angles are used in many different branches of physics and engineering. The present article is written from the point of view of molecular physics, where the objects to be rotated are [[molecules]]. | ||
==Geometric discussion== | ==Geometric discussion== | ||
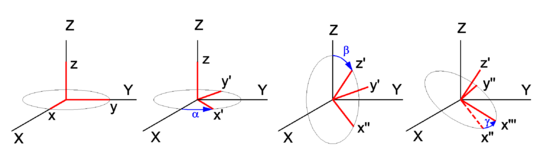
In | In Figure 1 the space-fixed (laboratory) axes are labeled by capital X, Y, and Z and are shown in black. The body to be rotated is not shown, but a system of axes fixed to it is shown in red. One may use any convenient orthonormal frame as a body-fixed frame. Often the body-fixed axes are [[principal axes]], that means that they are [[eigenvectors]] of the [[inertia tensor]] of the body. Also symmetry axes, when present, may be used. When the body has symmetry axes, the principal axes often coincide with these. | ||
The ''z-y′-z′'' convention will be followed. Initially, the two frames coincide, and the path to a final arbitrary orientation of the body—and its frame—is depicted on Figure 1. The first rotation is around the ''z''-axis, which coincides with the Z-axis. The ''x''- and ''y''-axis move in the circle perpendicular to the ''z''-axis over an angle α. The second rotation is around a circle perpendicular to the ''y′''-axis. The angle is β. It is a great practical advantage of the present convention that the ''z′''-axis has the usual [[spherical polar coordinates]] α ≡ φ (longitude angle) and β ≡ θ (colatitude angle) with respect to the space-fixed frame. | |||
(Due to this fact the complex conjugate of the ''m = 0'' column of the [[Wigner D-matrix]] consists of [[spherical harmonics]]). | |||
The final rotation is in a circle perpendicular to the ''z′''-axis over an angle γ. From geometric considerations follows that any orientation in space of the body-fixed frame may be obtained. | The final rotation is in a circle perpendicular to the ''z′''-axis over an angle γ. From geometric considerations follows that any orientation in space of the body-fixed frame may be obtained. | ||
We write <math>\mathbf{R}(\varphi, \hat{n})</math> for the [[rotation matrix]] that describes a rotation around the unit vector <math>\hat{n}</math> over an angle <math>\varphi</math>. | |||
Clearly the three consecutive Euler rotations correspond to rotations around | |||
the unit vectors along the body-fixed axes ''z'', ''y′'', and ''z′'' over angles α β, and γ, respectively. Because a matrix acts on a column vector to its right, the order in the matrix product is as in the rightmost term in the following equation. | |||
It will be shown that the corresponding matrix product can be written in reverse order (but around fixed, unprimed, axes ''z'', ''y'', ''z''), that is, | |||
:<math> | :<math> | ||
\mathbf{R}(\ | \begin{align} | ||
\mathbf{R}(\gamma, \hat{e}_{z'}) \mathbf{R}(\beta, \hat{e}_{y'}) \mathbf{R}(\alpha, \hat{e}_{z})&= | |||
\mathbf{R}(\alpha, \hat{e}_{z }) \mathbf{R}(\beta, \hat{e}_{y }) \mathbf{R}(\gamma, \hat{e}_{z}) \\ | |||
&= | |||
\begin{pmatrix} | |||
\cos\alpha & -\sin \alpha & 0 \\ | |||
\sin\alpha & \cos \alpha & 0 \\ | |||
0 & 0 & 1 \\ | |||
\end{pmatrix} | |||
\begin{pmatrix} | |||
\cos\beta & 0 & \sin\beta \\ | |||
0 & 1 & 0 \\ | |||
-\sin\beta & 0 & \cos\beta \\ | |||
\end{pmatrix} | |||
\begin{pmatrix} | |||
\cos\gamma & -\sin\gamma & 0 \\ | |||
\sin\gamma & \cos\gamma & 0 \\ | |||
0 & 0 & 1 \\ | |||
\end{pmatrix} \\ | |||
&= | |||
\begin{pmatrix} | |||
\cos\alpha\cos\beta\cos\gamma-\sin\alpha\cos\gamma \;&\; -\cos\alpha\cos\beta\sin\gamma-\sin\alpha\cos\gamma \;&\;\cos\alpha\sin\beta \\ | |||
\sin\alpha\cos\beta\cos\gamma+\cos\alpha\sin\gamma \;&\; -\sin\alpha\cos\beta\sin\gamma+\cos\alpha\cos\gamma \;&\; \sin\alpha\sin\beta \\ | |||
-\sin\beta\cos\gamma \;&\; \sin\beta\sin\gamma \;&\; \cos\beta | |||
\end{pmatrix} | |||
\end{align} | |||
</math> | </math> | ||
<!-- | |||
Further | Further | ||
:<math> | :<math> | ||
| Line 40: | Line 61: | ||
\mathbf{R}(\beta, \hat{e}_{y'})^{\mathrm{T}} | \mathbf{R}(\beta, \hat{e}_{y'})^{\mathrm{T}} | ||
</math> | </math> | ||
In [[this article]] it is shown that if '''A''' is a rotation matrix, that | |||
:<math> | |||
\mathbf{R}(\varphi, \mathbf{A}\hat{n}) = \mathbf{A}\mathbf{R}(\varphi, \hat{n})\mathbf{A}^{\mathrm{T}} | |||
</math> | |||
where the superscript T indicates the transpose of the matrix. For rotation matrices it holds that the transposed matrix is equal to the inverse of the matrix. | |||
--> | |||
Revision as of 06:17, 11 July 2009
In physics, mathematics, and engineering, Euler angles are three rotation angles, commonly denoted by 0 ≤ α ≤ 2π, 0 ≤ β ≤ π, and 0 ≤ γ ≤ 2π. Any rotation of a 3-dimensional object can be performed by three consecutive rotations over the three Euler angles.
Different conventions are in use: a rotation can be active (the object is rotated, the system of axes is fixed in space), or passive (the object is fixed in space, the axes are rotated).
The order of Euler angles may vary; a very common active convention is the z-y′-z′ convention. Attach a system of Cartesian coordinate axes to the body that is to be rotated (the coordinate frame is fixed to the body and is rotated simultaneously with it); in the figure the body-fixed frame is shown in red and labeled by lowercase letters. First rotate around z, then around the new body-fixed y-axis, y′, and finally around z′. Another convention often used is the z-x′-z′ convention, where instead of over the new y-axis the second rotation is over the new x-axis. Also the x-y′-z′′ convention is used.
The right-hand screw rule is practically always followed: the rotation axis is a directed line and a positive rotation is as a cork screw driven into the positive direction of the axis.
Euler angles are used in many different branches of physics and engineering. The present article is written from the point of view of molecular physics, where the objects to be rotated are molecules.
Geometric discussion
In Figure 1 the space-fixed (laboratory) axes are labeled by capital X, Y, and Z and are shown in black. The body to be rotated is not shown, but a system of axes fixed to it is shown in red. One may use any convenient orthonormal frame as a body-fixed frame. Often the body-fixed axes are principal axes, that means that they are eigenvectors of the inertia tensor of the body. Also symmetry axes, when present, may be used. When the body has symmetry axes, the principal axes often coincide with these.
The z-y′-z′ convention will be followed. Initially, the two frames coincide, and the path to a final arbitrary orientation of the body—and its frame—is depicted on Figure 1. The first rotation is around the z-axis, which coincides with the Z-axis. The x- and y-axis move in the circle perpendicular to the z-axis over an angle α. The second rotation is around a circle perpendicular to the y′-axis. The angle is β. It is a great practical advantage of the present convention that the z′-axis has the usual spherical polar coordinates α ≡ φ (longitude angle) and β ≡ θ (colatitude angle) with respect to the space-fixed frame. (Due to this fact the complex conjugate of the m = 0 column of the Wigner D-matrix consists of spherical harmonics). The final rotation is in a circle perpendicular to the z′-axis over an angle γ. From geometric considerations follows that any orientation in space of the body-fixed frame may be obtained.
We write for the rotation matrix that describes a rotation around the unit vector over an angle . Clearly the three consecutive Euler rotations correspond to rotations around the unit vectors along the body-fixed axes z, y′, and z′ over angles α β, and γ, respectively. Because a matrix acts on a column vector to its right, the order in the matrix product is as in the rightmost term in the following equation. It will be shown that the corresponding matrix product can be written in reverse order (but around fixed, unprimed, axes z, y, z), that is,
(To be continued)
Algebraic treatment
A proper rotation matrix R can be factorized thus
which is referred to as the Euler z-y-x parametrization, or also as
the Euler z-y-z parametrization.
Here the matrices representing rotations around the z, y, and x axis, respectively, over arbitrary angle φ, are
Proof
First the Euler z-y-x-parametrization will be proved by describing an algorithm for the factorization of R. Consider to that end the matrix product
The columns of the matrix product are for ease of reference designated by a1, a2, and a3. Note that the multiplication by Rx(ω1) on the right does not affect the first column, so that a1 = r1 (the first column of the matrix to be factorized). Solve and from the first column of R,
This is possible. First solve for from
Then solve for from the two equations:
Knowledge of and determines the vectors a2 and a3.
Since a1, a2 and a3 are the columns of a proper rotation matrix they form an orthonormal right-handed system. The plane spanned by a2 and a3 is orthogonal to and hence the plane contains and . Thus the latter two vectors are a linear combination of the first two,
Since are known unit vectors we can compute
These equations give with .
Augment the 2×2 matrix to the 3×3 matrix , then
This concludes the proof of the z-y-x parametrization.
The Euler z-y-z parametrization is obtained by a small modification of the previous proof. Solve and from (the rightmost multiplication by Rz(ω1) does not affect r3) and then consider
or, The equation for R can be written as
which proves the Euler z-y-z parametrization. It is common in this parametrization to write
(To be continued)