Sensitivity and specificity
The sensitivity and specificity of diagnostic tests are based on Bayes Theorem and defined as "measures for assessing the results of diagnostic and screening tests. Sensitivity represents the proportion of truly diseased persons in a screened population who are identified as being diseased by the test. It is a measure of the probability of correctly diagnosing a condition. Specificity is the proportion of truly nondiseased persons who are so identified by the screening test. It is a measure of the probability of correctly identifying a nondiseased person. (From Last, Dictionary of Epidemiology, 2d ed)."[1]
Successful application of sensitivity and specificity is an important part of practicing evidence-based medicine.
Calculations
| Disease | ||||
|---|---|---|---|---|
| Present | Absent | |||
| Test result | Positive | Cell A | Cell B | Total with a positive test |
| Negative | Cell C | Cell D | Total with a negative test | |
| Total with disease | Total without disease | |||
Many of these calculations can be done at http://statpages.org/ctab2x2.html.
Sensitivity and specificity
Predictive value of tests
The predictive values of diagnostic tests are defined as "in screening and diagnostic tests, the probability that a person with a positive test is a true positive (i.e., has the disease), is referred to as the predictive value of a positive test; whereas, the predictive value of a negative test is the probability that the person with a negative test does not have the disease. Predictive value is related to the sensitivity and specificity of the test."[2]
Summary statistics for diagnostic ability
While simply reporting the accuracy of a test seems intuitive, the accuracy is heavily influenced by the prevalence of disease.[3] For example, if the disease occurred with frequency of one in one thousand, then simply guessing that all patients do not have disease will yield an accuracy of over 99%, whereas if the disease frequency were 999 in one thousand, the same guess would yield an accuracy near 1%.
With the arrival of many biomarkers that may be expensive diagnostic tests, much research has addressed how to summarize the incremental value of a new expensive test to existing diagnostic methods.[4][5][6] The best method to compare diagnostic tests depends on whether the new test is to replace or add to the existing diagnostic test.[7]
Area under the ROC curve
The area under the receiver operating characteristic curve (ROC curve), AROC, or c-index has been proposed. The c-index varies from 0 to 1 and a result of 0.5 indicates that the diagnostic test does not add to guessing.[8] Variations have been proposed.[9][10]
Bayes Information Criterion
The Bayes Information Criterion has been proposed by Schwarz in 1978.[11]
Diagnostic odds ratio
The diagnostic odds ratio (DOR) is based on the likelihood ratios.[12]
Whereas the likelihood ratio is:[13]
The diagnostic odds ratio is:[13]
Or the diagnostic odds ratio is:
For example:
- If the sensitivity and specificity are 95% and 80%, respectively (or vice versa) then the DOR = 71.
- If the sensitivity and specificity are both 95%, then the DOR = 361.
"The DOR ranges from 0 to infinity, with higher values indicating better discriminatory test performance. A value of 1 means that a test does not discriminate between patients with the disorder and those without it... The DOR does not depend on the prevalence of the disease."[12]
Sum of sensitivity and specificity
This easy metric is called the Gain in Certainty:[14]
It varies from 0 to 2 and a result of 1 indicates that the diagnostic test does not add to guessing.
Similarly, Youden's J index (J*), is:[15]
The index is derived from:
Number needed to diagnose
The number needed to diagnose is:[16]
Predictiveness curve
A graph of the predictiveness curve has been proposed.[17]
Proportionate reduction in uncertainty score
The proportionate reduction in uncertainty score (PRU) has been proposed.[18]
Integrated sensitivity and specificity
This measure has been proposed as an alternative to the area of the the receiver operating characteristic curve.[19]
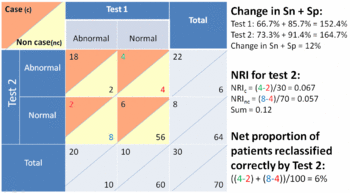
Reclassification tables
This measure has been proposed as an alternative to the area of the the receiver operating characteristic curve.[4][19] This method allows calculating a 'reclassification index' or 'reclassification rate', or 'net reclassification improvement' (NRI).[19]
The NRI is analogous to Youden's J index and the Gain in Certainty which are both functions of the sum of the sensitivity and specificity. In the special case of two diagnostic tests that have binary results (e.g. normal and abnormal), the NRI is the same the Gain in Certainty of the first test minus the Gain in Certainty of the second test, or alternatively stated, the change in the sum of the sensitivity and specificity:
Both the NRI, Youden's J, and the Gain in Certainty are measures that:
- Assume the importance of correctly classifying a abnormal patient is equally as important as correctly classifying a normal patient
- Sum two rates (sensitivity and specificity) rather than a weighted average the two rates based on the ratio of abnormal to normal patients.
- Summing helps compare two tests that were studied in settings with different prevalences of disease.
- However, the NRI may be seen as misleading as it is an index of reclassification and not a rate of reclassification. In the special case of a prevalence of disease of 50%, the index of reclassification is exactly double the rate of reclassification.
The clinical net reclassification improvement (CNRI) is a variation that is the NRI only for the subjects at intermediate risk of disease.[6]
Sequential scoring
Sequential scoring has been proposed in order to isolate the effect of a new, expensive diagnostic test.[20]
Threats to validity of calculations
Various biases incurred during the study and analysis of a diagnostic tests can affect the validity of the calculations. An example is spectrum bias.
Poorly designed studies may overestimate the accuracy of a diagnostic test.[21]
References
- ↑ National Library of Mediicne. Sensitivity and specificity. Retrieved on 2007-12-09.
- ↑ National Library of Mediicne. Predictive value of tests. Retrieved on 2007-12-09.
- ↑ Harrell FE, Califf RM, Pryor DB, Lee KL, Rosati RA (May 1982). "Evaluating the yield of medical tests". JAMA 247 (18): 2543–6. PMID 7069920. [e]
- ↑ Jump up to: 4.0 4.1 Cook NR, Ridker PM (June 2009). "Advances in measuring the effect of individual predictors of cardiovascular risk: the role of reclassification measures". Ann. Intern. Med. 150 (11): 795–802. PMID 19487714. [e]
- ↑ Cornell J, Mulrow CD, Localio AR (December 2008). "Diagnostic test accuracy and clinical decision making". Ann. Intern. Med. 149 (12): 904–6. PMID 19075211. [e]
- ↑ Jump up to: 6.0 6.1 Cook NR (January 2008). "Comments on 'Evaluating the added predictive ability of a new marker: From area under the ROC curve to reclassification and beyond' by M. J. Pencina et al., Statistics in Medicine (DOI: 10.1002/sim.2929)". Stat Med 27 (2): 191–5. DOI:10.1002/sim.2987. PMID 17671959. Research Blogging.
- ↑ Hayen A, Macaskill P, Irwig L, Bossuyt P (2010). "Appropriate statistical methods are required to assess diagnostic tests for replacement, add-on, and triage.". J Clin Epidemiol. DOI:10.1016/j.jclinepi.2009.08.024. PMID 20079607. Research Blogging.
- ↑ Hanley JA, McNeil BJ (April 1982). "The meaning and use of the area under a receiver operating characteristic (ROC) curve". Radiology 143 (1): 29–36. PMID 7063747. [e]
- ↑ Walter SD (July 2005). "The partial area under the summary ROC curve". Stat Med 24 (13): 2025–40. DOI:10.1002/sim.2103. PMID 15900606. Research Blogging.
- ↑ Bangdiwala SI, Haedo AS, Natal ML, Villaveces A (September 2008). "The agreement chart as an alternative to the receiver-operating characteristic curve for diagnostic tests". J Clin Epidemiol 61 (9): 866–74. DOI:10.1016/j.jclinepi.2008.04.002. PMID 18687288. Research Blogging.
- ↑ Schwarz, G. (1978). Estimating the dimension of a model. Annals of Statistics 6, 461–464. DOI:10.1214/aos/1176344136 Google Scholar
- ↑ Jump up to: 12.0 12.1 Glas AS, Lijmer JG, Prins MH, Bonsel GJ, Bossuyt PM (November 2003). "The diagnostic odds ratio: a single indicator of test performance". J Clin Epidemiol 56 (11): 1129–35. PMID 14615004. [e]
- ↑ Jump up to: 13.0 13.1 SGIM EBM Task Force and Interest Group (2009). Ask the EBM Expert! - Society of General and Internal Medicine (SGIM). Society of General Internal Medicine.
- ↑ Connell FA, Koepsell TD (May 1985). "Measures of gain in certainty from a diagnostic test". Am. J. Epidemiol. 121 (5): 744–53. PMID 4014166. [e]
- ↑ Youden WJ (January 1950). "Index for rating diagnostic tests". Cancer 3 (1): 32–5. PMID 15405679. [e]
- ↑ Bandolier (1996) How Good is that Test? II
- ↑ Pepe, Margaret S.; Ziding Feng, Ying Huang, Gary Longton, Ross Prentice, Ian M. Thompson, Yingye Zheng (2008-02-01). "Integrating the Predictiveness of a Marker with Its Performance as a Classifier". Am. J. Epidemiol. 167 (3): 362-368. DOI:10.1093/aje/kwm305. PMID 17982157. Retrieved on 2008-12-17. Research Blogging.
- ↑ Coulthard MG (May 2007). "Quantifying how tests reduce diagnostic uncertainty". Arch. Dis. Child. 92 (5): 404–8. DOI:10.1136/adc.2006.111633. PMID 17158858. Research Blogging.
- ↑ Jump up to: 19.0 19.1 19.2 Pencina MJ, D'Agostino RB, D'Agostino RB, Vasan RS (January 2008). "Evaluating the added predictive ability of a new marker: from area under the ROC curve to reclassification and beyond". Stat Med 27 (2): 157–72; discussion 207–12. DOI:10.1002/sim.2929. PMID 17569110. Research Blogging.
- ↑ Greenland S (January 2008). "The need for reorientation toward cost-effective prediction: comments on 'Evaluating the added predictive ability of a new marker: From area under the ROC curve to reclassification and beyond' by M. J. Pencina et al., Statistics in Medicine (DOI: 10.1002/sim.2929)". Stat Med 27 (2): 199–206. DOI:10.1002/sim.2995. PMID 17729377. Research Blogging.
- ↑ Lijmer JG, Mol BW, Heisterkamp S, et al (September 1999). "Empirical evidence of design-related bias in studies of diagnostic tests". JAMA 282 (11): 1061–6. PMID 10493205. [e]