Molecular orbital
In quantum chemistry, a molecular orbital (MO) is a one-electron function that is "smeared out" over a whole molecule. Usually an MO is a linear combination of atomic orbitals (an LCAO), which is a weighted sum of (almost) all atomic orbitals in the molecule. Molecular symmetry plays an important role in molecular orbital theory. In general MOs are adapted to symmetry, which has the consequence that atomic orbitals of a symmetry different than that of an MO do not contribute to the MO (have weight factor zero).
The expansion coefficients (weight factors) of an MO can be determined by semi-empirical molecular orbital theory, which may or may not be of the self-consistent field type, or by ab initio methods. The most common ab initio method for determining MO coefficients is the self-consistent field method of Hartree and Fock. Lately, density functional theory methods for computing MOs have found increasing application.
Definition of molecular orbital
A molecular orbital (MO) depends on several position vectors of one and the same electron, labeled 1: rA1, rB1, rC1, ... where A, B, C, ... are different points in space (usually nuclear positions). The oldest example of an MO (without use of the name MO yet) is in the work of Burrau (1927) on the single-electron ion H2+. Burrau applied spheroidal coordinates (a bipolar coordinate system) to describe the wave functions of the electron of H2+.
Lennard-Jones[1] introduced the following linear combination of atomic orbitals (LCAO) way of writing an MO φ:
where A runs over Nnuc different points in space (usually A runs over all the nuclei of a molecule, hence the name molecular orbital), and i runs over the nA different AOs centered at A. The complex coefficients c Ai can be calculated by any of the existing effective-one-electron quantum chemical methods. Examples of such methods are the Hückel method—a non-self-consistent field method— and the Hartree-Fock method—a self-consistent field method.
Computation of molecular orbitals
- See also Heitler-London theory for an account of the chemical bond in H2.
In the hands of Friedrich Hund, Robert S. Mulliken, John Lennard-Jones, and others, molecular orbital theory was established firmly in the 1930s as a (mostly qualitative) theory explaining much of chemical bonding, especially the bonding in diatomic molecules.
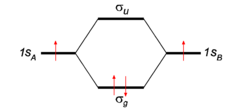
To give the flavor of the theory we look at the simplest molecule: H2. The two hydrogen atoms, labeled A and B, each have one electron (a red arrow in the figure) in an 1s atomic orbital (AO). These AOs are labeled in the figure 1sA and 1sB. When the atoms start to interact the AOs combine linearly to two molecular orbitals:
In equation (1) above a general expression for an LCAO-MO is given. In the present example of the σg MO of H2, we have Nnuc = 2, nA = nB = 1, χA1 = 1sA, χB1 = 1sB, cA1 = cB1 = Ng. With regard to the form of the MOs the following: Because both hydrogen atoms are identical, the molecule has reflection symmetry with respect to a mirror plane halfway the H—H bond and perpendicular to it. It is one of the basic assumptions in quantum mechanics that wave functions show the symmetry of the system. [Technically: solutions of the Schrödinger equation belong to a subspace of Hilbert (function) space that is irreducible under the symmetry group of the system]. Clearly σg is symmetric (is even, stays the same) under
while σu changes sign (is antisymmetric, is odd). The Greek letter σ indicates invariance under rotation around the bond axis. The subscripts g and u stand for the German words gerade (even) and ungerade (odd). So, because of the high symmetry of the molecule we can immediately write down two molecular orbitals, which evidently are linear combinations of atomic orbitals.
The normalization factors Ng and Nu and the orbital energies are still to be computed. The normalization constants follow from requiring the MOs to be normalized to unity. In the computation we will use the bra-ket notation for the integral over xA1, yA1, and zA1 (or over xB1, yB1, and zB1 when that is easier).
We used here that the AOs are normalized to unity and that the overlap integral is real
Applying the same procedure for Nu, we find for the two normalization factors
At this point one often assumes that S ≈ 0, so that both normalization factors are equal to ½√2.
In order to calculate the energy of an orbital we introduce an effective-one-electron energy operator (Hamiltonian) h,
Since A and B are identical atoms equipped with identical AOs, we were allowed to use
Likewise
The energy term β is negative (causes the attraction between the atoms). One may tempted to assume that q = −½ hartree (the energy of the 1s orbital in the free atom). This is not the case, however, because h contains the attraction with both nuclei, so that q is distance dependent.
If we now look at the figure in which energies are increasing in vertical direction, we see that the two AOs are at the same energy level q, and that the energy of σg is a distance |β| below this level, while the energy of σu is a distance |β| above this level. In the present simple-minded effective-one-electron model we can simply add the orbital energies and find that the bonding energy in H2 is 2β (two electrons in the bonding MO σg, ignoring the distance dependence of q). This model predicts that the bonding energy in the one-electron ion H2+ is half that of H2, which is correct within a 20% margin.
If we apply the model to He2, which has four electrons, we find that we must place two electrons in the bonding orbital and two electrons in the antibonding MO σu, with the total energy being 2β − 2β = 0. So, this simple application of molecular orbital theory predicts that H2 is bound and that He2 is not, which is in agreement with the observed facts.
References
- ↑ J. E.Lennard-Jones, The Electronic Structure of some Diatomic Molecules. Trans. Faraday Soc., vol 25, p. 668 (1929).





![{\displaystyle N_{g}=\left[2+2S\right]^{-1/2}\quad {\hbox{and}}\quad N_{u}=\left[2-2S\right]^{-1/2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a8195f74219ed9fb2d24bded62392e7730dd0a1)


