Relative permeability
In physics, in particular in magnetostatics, the relative permeability is an intrinsic property of a magnetic material. It is usually denoted by μr. For simple magnetic materials, using SI units, μr is related to the proportionality constant between the magnetic flux density B and the magnetic field H, namely B = μr μ0 H, where μ0 is the magnetic constant. The relative permeability describes the ease by which a magnetic medium may be magnetized.
A related quantity is the magnetic susceptibility, denoted by χm, related to the relative permeability in SI units by:[1]
The relative permittivity μr may be greater than or less than 1. For simple media, if μr < 1 (χm negative), the medium is termed diamagnetic; if μr > 1 (χm positive) paramagnetic. Only classical vacuum has μr = 1 (exact). A typical diamagnetic susceptibility is about −10−5, while a typical paramagnetic susceptibility is about 10−4.
Relation to magnetization
The magnetic flux density B is related to the magnetization of a magnetic medium M as:
In a simple magnetic material, the magnetization induced by H is simply proportional to the field H, and is given in terms of the medium's magnetic susceptibility as:
Consequently, the magnetic flux density in such a magnetic medium is simply:
Here μ is referred to as the magnetic permeability.
In implementing these relations, it should be noted that the use of a constant as the relative permeability of a substance is an approximation, even for quantum vacuum. A more complete representation recognizes that all media exhibit departures from this approximation, in particular, a dependence on field strength, a dependence upon the rate of variation of the field in both time and space, and a dependence upon the direction of the field. In many materials these dependencies are slight; in others, like ferromagnets, they are pronounced.
Relation to forces
See also Ampère's equation.
Similar to Coulomb's law describing the electric force between electric charges, the magnetic force between two magnetic poles of pole strength given by p1 and p2 and separated by distance r in a medium of relative permeability μr has magnitude F:
and is directed along the line joining the poles. It is attractive if the poles are opposite in nature (one north pole and one south pole) and repulsive if they are the same.
It happens, however, that magnetic poles always occur as opposite pairs, so the force law between single poles cannot be observed directly. However, magnetic dipoles do occur in nature and can be directly observed. A planar wire loop conducting a steady electric current resembles a magnetic dipole at distances large compared to the dimensions of the loop.
The magnetic force between two point charges moving at constant velocity (or for accelerating charges with velocities well below the speed of light) in a medium of relative permeability μr is provided by the Lorentz force acting upon one charge via the magnetic flux density generated by the other as predicted by the Biot-Savart law.[2] (It should be born in mind that point charges do not exist in nature: when a charge has dimensions, things become much more complicated.) Let the charges be q1, q2, their separation be r12, and their constant velocities be v1, v2. The magnetic flux density B generated by charge 2 at a position P in classical vacuum is:[3]
where û is a unit vector pointing from the charge to the field evaluation point P, and r is the distance between the charge and the field point. The corresponding magnetic field H is:
If now the charges are placed in a magnetic medium, the field H induces a magnetization M in the medium, and within the assumption of a simple linear magnetic material M = χmμ0 H. Thus, the medium changes B = μ0H to B = μ0(1+χm)H and the flux density in the medium becomes:
Then the magnetic force upon charge 1 located at P1 due to charge 2 according to the Lorentz law is:[4]
where û12 is a unit vector pointing from charge 2 to charge 1 and r12 is their separation. This expression can be expressed in terms of the normal scalar products of the vectors using the baccab formula for the triple vector product:
This expression does not satisfy Newton's law of action and reaction, which would require the force on charge 1 due to charge 2 be equal and opposite to the force on particle 2 due to charge 1. But it does not have to, because it does not describe an instantaneous action-at-a-distance, but rather, a force mediated by propagation of the electromagnetic field.
This relation is closely connected to the force between two current elements, as described by Grassmann's adaptation of Ampère's equation, described next.
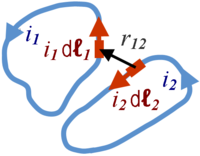
The force exerted between infinitesimal current elements from two loops carrying steady currents ii and ij and immersed in a magnetic medium with relative permeability μr is changed by a factor μr. The infinitesimal current elements have vector components i1dℓ1 and i2dℓ2 where the incremental lengths are directed along the wire at the location of the element, and pointing in the direction of the current. Grassmann's law for the force upon current element 1 exerted by current element 2 is:[5]
as is readily derived from the Biot-Savart law, and is consistent with space-time symmetry. Here û12 is a unit vector pointing from element 2 to element 1 along the line joining them, and r12 the length of this line. The force element is second order because it is a product of two infinitesimals.
Background
Maxwell reduced electrodynamics to the knowledge of charge and current distributions, and introduced the notion of material properties (constitutive relations) relating magnetic flux density B to magnetic field H and electric displacement D to electric field E.
Notes
- ↑ For example see Yehuda Benzion Band. Light and matter: electromagnetism, optics, spectroscopy and lasers. John Wiley and Sons, p. 242. ISBN 0471899313.
- ↑ A magnetic field varying as the inverse square of distance applies for a point charge moving with constant velocity of any magnitude. The expression given as the Biot-Savart law, however, ignores factors involving v/c so applies only when v/c is negligible. For an accelerating point charge, the magnetic field is not described by the Biot-Savart law because there is an additional radiation field. See, for example, Harald J. W. Müller-Kirsten (2004). “§10.4 The fields E, B of a moving point charge”, Electrodynamics: an introduction including quantum effects. World Scientific, p. 223. ISBN 9812388087. or Robert Joseph Gould (2006). “§2.4.2: Charge in uniform motion”, Electromagnetic processes. Princeton University Press. ISBN 0691124442.
- ↑ Paul A. Tipler (1998). “The magnetic field of moving point charges”, Physics for Scientists and Engineers, Parts 1-35; Part 39, 4rth ed. W. H. Freeman, p. 884. ISBN 9781572594920.
- ↑ John A. Camara (2010). “§22: Biot-Savart law”, Power Reference Manual for the Electrical and Computer PE Exam. Professional Publications, Inc., p. 16-15. ISBN 1591261627.
- ↑ See for example, André KT Assis (1995). “Equation (9)”, Julian B. Barbour, Herbert Pfister, eds: Mach's principle: from Newton's bucket to quantum gravity. Birkhäuser Publishers, p. 162. ISBN 0817638237.