Logarithm

Computing logarithms is the inverse of exponentiation, as subtraction is the inverse of addition and division is the inverse of multiplication. For example, since $343=7^{3}$, then the base-7 logarithm of 343 is 3. In general, if $a=b^{c}$, then $\log _{b}(a)=c$.

Because we use a base-10 number system, it is often convenient to use 10 as the base of the logarithm. Multiplying a number by 10 appends a zero to the numeral and adds 1 to the logarithm. For example, $\log _{10}(43)$ is approximately equal to 1.63347, and multiplying by 10, $\log _{10}(430)$ is approximately 2.63347.

Mathematicians and physicists often find, however, that the transcendental number $e$ is more convenient as a base for a logarithmic function. The value of $e$ is approximately equal to 2.718281828459045. The logarithmic function with $e$ as a base is called the "natural logarithm" and is often written $\ln(x)$; it is the function whose derivative is $1/x$.

Extension of logarithms to fractional and negative values

Originally, exponents were natural numbers: it's easy to see the meaning of an expression such as $10^{3}=10\times 10\times 10$. Rules for adding and multiplying exponents were noticed, and to extend the idea to fractions and negative numbers it was assumed that the same rules would apply. To define a meaning for a fractional value such as $10^{\frac {1}{2}}$, consider that, using a rule for multiplying exponents,

$(10^{\frac {1}{2}})^{2}=10^{{\frac {1}{2}}\times 2}=10^{1}=10$

Therefore $10^{\frac {1}{2}}$ must be ${\sqrt {10}}$ and this then supplies a value for $\log _{10}({\sqrt {10}})=0.5$. Values for many other numbers can be worked out similarly using cube roots and so on, and values for all real numbers can then be defined using limits.

To assign meaning to negative values of exponents, note the rule that

$b^{x}b^{y}=b^{x+y}.$

So, for example, to find the meaning of $10^{-3}$, consider

$10^{-3}\times 10^{4}=10^{-3+4}=10^{1}=10$

Therefore,

$10^{-3}={\frac {10}{10^{4}}}=0.001$

and it then follows that

$\log _{10}(0.001)=-3,$

or in general,

$\log _{b}\left({\frac {1}{x}}\right)=-\log _{b}(x).$

By a similar argument it can be established that $b^{0}=1$ for any base $b>1$ and therefore that $\log _{b}(1)=0$.

Thus, logarithms of numbers between 0 and 1 are negative numbers, the logarithm of 1 is 0, and logarithms of numbers that fall between powers of the base are (usually non-integer) real numbers.

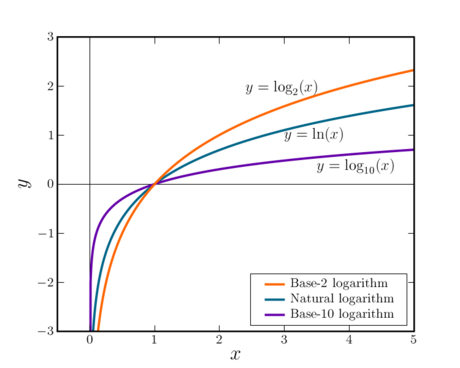
Shape of the logarithm function

Consider the function $f(x)=\log _{b}(x)$ where b is a real-number base greater than 1 of the logarithm. Since any positive real number raised to the exponent zero is 1, the logarithm of 1 is zero. To the right of 1 on the x-axis, the function $f$ continually increases, but increases more and more slowly as $x$ heads towards infinity. Between 1 and 0, the logarithmic function has negative values, and asymptotically approaches minus infinity as $x$ approaches zero. For negative values of $x$, there is no defined value of $f(x)$ within the real numbers — but using complex numbers a value can be found, as will be discussed further below.

Manipulating logarithms

Suppose we know the logarithm of a number using one base $b$, and we want to find the logarithm using a different base $c$ :

$\log _{b}(x)=y$

$\log _{c}(x)=$?

Suppose we know $y$, $b$ and $c$ and we want to find $\scriptstyle {\log _{c}(x)}$. We need to look up the value of $\log _{c}(b)$, and then by multiplying we can find the desired quantity:

$\log _{c}(x)=\log _{c}(b)\log _{b}(x)$

This formula can be established using the definition of logarithms and the rule for multiplying exponents:

$x=b^{\log _{b}x}$

$b=c^{\log _{c}b}$

Substituting for b,

$x=(c^{\log _{c}b})^{\log _{b}x}$

$x=c^{\log _{c}(b)\log _{b}(x)}$

Therefore $\log _{c}(x)=\log _{c}(b)\log _{b}(x)$, the formula we wished to prove.

A useful formula for $\log(xy)$ can be derived using the rule for adding exponents:

$b^{\log _{b}(xy)}=xy=b^{\log _{b}x}b^{\log _{b}y}=b^{\log _{b}x+\log _{b}y}$

Therefore :

$\log _{b}(xy)=\log _{b}(x)+\log _{b}(y)$

Notational Variants

When logarithms are used to measure physical values (e.g., when noise is measured in deciBels) it is common to use 10 as a base, and in these contexts, the notation $\scriptstyle \log x$ means $\scriptstyle \log _{10}\,x$. In mathematics, it is more useful to use natural logarithms (i.e., logarithms to the base of $e$). The notation $\scriptstyle \ln x$ is sometimes used for natural logarithms, but in mathematics it is just as common to use the notation $\log \,x$ and write logarithms to base 10 using the full notation $\scriptstyle \log _{10}\,x$. Computer science adds a whole new wrinkle because, in some cases, it is most useful to consider logarithms to base 2, and this has led to a new notation $\mathrm {lg} \,x$ which become common for logarithms to a base of 2. Finally, the notation $\scriptstyle \log \,x$ is sometimes used for logarithms to base 2, but this is usage is less common.

Complex numbers and logarithms

The exponential function of an imaginary number is given as

$e^{ix}=\cos(x)+i\sin(x).\,$

To find the logarithm of a complex number $a+bi$, it's convenient to express the number in polar coordinates $(r,\theta )$ where $\scriptstyle r={\sqrt {a^{2}+b^{2}}}$ and $\theta =\arctan(b/a)$. (Intuitively, $r$ is the length of the line segment joining the number to the origin in the complex plane, and $\theta$ is the angle that line segment makes with the $x$-axis.) The equivalence of the two notations is given by

$a+bi=r(\cos(\theta )+i\sin(\theta )).\,$

Suppose we define $c+di$ such that $\ln(a+bi)=c+di$. Using the formula for the exponential function above,

$a+bi=e^{c+di}=e^{c}e^{di}=e^{c}(\cos(d)+i\sin(d))\,$

It can be seen from similarity with the above formula for polar coordinates that $\scriptstyle {r=e^{c}}$ and $\scriptstyle {d=\theta }$. Therefore,

$\ln(a+bi)=c+di=\ln(r)+i\theta =\ln({\sqrt {a^{2}+b^{2}}})+i\arctan \left({\frac {b}{a}}\right).\,$

In this way, the logarithmic function can be extended to cover the entire complex plane except for the number zero, which has an undefined value — a singularity with the real part plunging towards minus infinity and the imaginary part spinning wildly.