Golden ratio: Difference between revisions
imported>Ro Thorpe mNo edit summary |
imported>Ro Thorpe mNo edit summary |
||
| Line 9: | Line 9: | ||
The earliest existing description is found in the [[Euclid's Elements|Elements]] of [[Euclid]] (Book 5, definition 3) in which says, ''A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the less.'' | The earliest existing description is found in the [[Euclid's Elements|Elements]] of [[Euclid]] (Book 5, definition 3) in which says, ''A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the less.'' | ||
According to | According to Merriam-Webster's Collegiate Dictionary, Eleventh Edition, the proportion is derived from two segments in which "the ratio of the whole to the larger part is the same as the ratio of the larger part to the smaller." | ||
To be more elaborate: if there is a longer line segment <math>\scriptstyle a\ </math> and and a shorter line segment <math>\scriptstyle b\ </math>, and if the ratio between <math>\scriptstyle a + b\ </math> and <math>\scriptstyle a\ </math> is equal to the ratio between the line segment <math>\scriptstyle a\ </math> and <math>\scriptstyle b\ </math>, this ratio is the golden ratio. The value of the golden ratio is <math>\scriptstyle \Phi = \frac{a}{b}= \frac{1 + \sqrt{5}}{2} = 1{,}618033988\dots</math> | To be more elaborate: if there is a longer line segment <math>\scriptstyle a\ </math> and and a shorter line segment <math>\scriptstyle b\ </math>, and if the ratio between <math>\scriptstyle a + b\ </math> and <math>\scriptstyle a\ </math> is equal to the ratio between the line segment <math>\scriptstyle a\ </math> and <math>\scriptstyle b\ </math>, this ratio is the golden ratio. The value of the golden ratio is <math>\scriptstyle \Phi = \frac{a}{b}= \frac{1 + \sqrt{5}}{2} = 1{,}618033988\dots</math> | ||
Revision as of 18:32, 8 September 2009
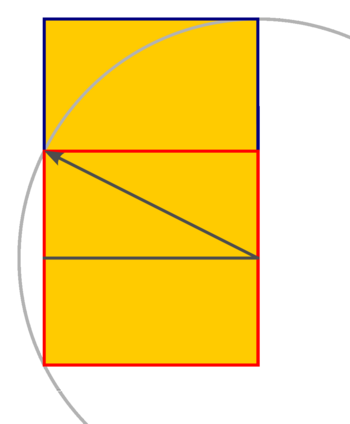
The golden ratio is a mathematical proportion that is important in the arts and interesting to mathematicians. In architecture and painting, some works have been proportioned to approximate the golden ratio ever since antiquity, when, supposedly, some of the buildings on the Acropolis derived their eye-pleasing aesthetics from the use of this ratio in determining the length of the buildings to their height and width. It is also known as the Mean and Extreme Ratio, the Golden Section, the Golden Mean, and the Divine Proportion.
The earliest existing description is found in the Elements of Euclid (Book 5, definition 3) in which says, A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the less.
According to Merriam-Webster's Collegiate Dictionary, Eleventh Edition, the proportion is derived from two segments in which "the ratio of the whole to the larger part is the same as the ratio of the larger part to the smaller."
To be more elaborate: if there is a longer line segment and and a shorter line segment , and if the ratio between and is equal to the ratio between the line segment and , this ratio is the golden ratio. The value of the golden ratio is
Properties
- If it follows that
With we could derive the infinite continued fraction of the golden ratio:
Thus
- ,
where is the n-th term of the Fibonacci sequence.