| The metadata subpage is missing. You can start it via filling in this form or by following the instructions that come up after clicking on the [show] link to the right.
|
Do you see this on PREVIEW? then SAVE! before following a link.
A - For a New Cluster use the following directions
Subpages format requires a metadata page.
Using the following instructions will complete the process of creating this article's subpages.
- Click the blue "metadata template" link below to create the page.
- On the edit page that appears paste in the article's title across from "
pagename =".
- You might also fill out the checklist part of the form. Ignore the rest.
- For background, see Using the Subpages template Don't worry--you'll get the hang of it right away.
- Remember to hit Save!
 the "metadata template". the "metadata template".
However, you can create articles without subpages. Just delete the {{subpages}} template from the top of this page and this prompt will disappear. :) Don't feel obligated to use subpages, it's more important that you write sentences, which you can always do without writing fancy code.
|
B - For a Cluster Move use the following directions
The metadata template should be moved to the new name as the first step. Please revert this move and start by using the Move Cluster link at the top left of the talk page.
The name prior to this move can be found at the following link.
|
|
//
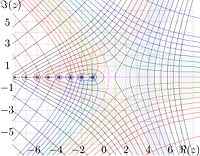
// Generator of figure http://en.citizendium.org/wiki/Image:LogFactorialZ.jpg
// plot of LogFactorial(z) in the complex z-plane.
// In order to complie this program, files
//ContourPlot/code/ado.cin (function that makes header of the eps file) and
//ContourPlot/code/conto.cin (function which draws a level) should be loaded.
//
// Copyleft 2009 by Dmitrii Kouznetsov
// Please, indicate the source and modifications (if any) at the use.
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
#include <complex.h>
#define z_type complex<double>
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
DB expaunoc[31]= {1.,
0.5772156649015329, -0.6558780715202537, -0.04200263503409518, 0.16653861138229112,
-0.04219773455554465, -0.009621971527877027, 0.0072189432466631676, -0.0011651675918590183,
-0.0002152416741149077, 0.00012805028238804805,-0.00002013485478102872,-1.2504934818746705e-6,
1.1330272320364543e-6, -2.0563384228733383e-7, 6.1160952968819515e-9, 5.00200766282674e-9,
-1.1812748557105124e-9, 1.0434320074637071e-10, 7.782441358017422e-12, -3.696820627396846e-12,
5.10702591327572e-13, -2.0650148258027912e-14,-6.217248937900877e-15, 7.771561172376096e-16,
-9.992007221626409e-16, -3.3306690738754696e-16, 5.551115123125783e-16, -1.1102230246251565e-16,
1.3322676295501878e-15, 9.992007221626409e-16 };
z_type expauno(z_type z) {int n,m; DB x,y; z_type s; s=expaunoc[24];
x=Re(z);if(x<-.9) return expauno(z+1.)-log(z+1.);
if(x>.5) return expauno(z-1.)+log(z);
y=Im(z); if(fabs(y)>.7)return expauno(z/2.)+expauno(z/2.-.5)+z*log(2.)-log(sqrt(M_PI));
for(n=23; n>=0; n--) { s*=z;s+=expaunoc[n]; }
return -log(s); }
z_type fracti(z_type z){ z_type s; int n; DB a[17]=
{0.0833333333333333333, 0.0333333333333333333, .252380952380952381, .525606469002695418,
1.01152306812684171, 1.51747364915328740, 2.26948897420495996, 3.00991738325939817,
4.02688719234390123, 5.00276808075403005, 6.28391137081578218, 7.49591912238403393,
9.04066023436772670, 10.4893036545094823, 12.2971936103862059, 13.9828769539924302, 16.0535514167049355
};
/* a[0]=1./12.; a[1]=1./30.; a[2]=53./210.; a[3]=195./371.; a[4]=22999./22737.; a[5]=29944523./19773142.;
a[6]=109535241009./48264275462.; a[7]=29404527905795295658./9769214287853155785.;
a[8]=455377030420113432210116914702./113084128923675014537885725485.;
a[9]=26370812569397719001931992945645578779849./5271244267917980801966553649147604697542.;
a[10]=152537496709054809881638897472985990866753853122697839./24274291553105128438297398108902195365373879212227726.;
a[11]= too long... */
//s=a[16]/(z+19./(z+25./(z+40.)));
s=a[16]/(z+19./(z+25./(z)));
for(n=15;n>=0;n--) s=a[n]/(z+s);
return s + log(2.*M_PI)/2. - z + (z+.5)*log(z);
}
z_type lofac(z_type z){DB x,y,r;
x=Re(z); y=Im(z);
if(fabs(y)>5 ) return fracti(z);
if(x>0 && (x-3)*(x-3.)+y*y >25) return fracti(z);
return expauno(z);
}
#include "conto.cin"
main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d, cu,cd;
int M=421,M1=M+1;
int N=361,N1=N+1;
DB X[M1],Y[N1], g[M1*N1],f[M1*N1], w[M1*N1]; // w is working array.
char v[M1*N1]; // v is working array
FILE *o;o=fopen("LogFactorialZ.eps","w");ado(o,0,0,182,142);
fprintf(o,"91 71 translate\n 10 10 scale\n");
DO(m,M1) X[m]=-8.2+.04*(m-.5);
DO(n,N1) Y[n]=-7. +.04*(n-.5);
for(m=-8;m<9;m++) { if(m==0){M(m,-6.2)L(m,6.2)} else {M(m,-6)L(m,6)} }
for(n=-6;n<7;n++) { M( -8,n)L(8,n)}
fprintf(o,".006 W 0 0 0 RGB S\n");
DO(m,M1)DO(n,N1){g[m*N1+n]=9999; f[m*N1+n]=9999;}
DO(m,M1){x=X[m]; // printf("%2.0fd\n",0.);
DO(n,N1){y=Y[n]; z=z_type(x,y);
c=lofac(z);
//c= fracti(z);
//d= expauno(z);
// d= exp(fracti(z))*(z+1.) ;
//p=abs(c-d)/(abs(c)+abs(d)); p=-log(p)/log(10.);
p=Re(c);q=Im(c);
if(p>-999 && p<999 && fabs(p)> 1.e-9 && fabs(p-1.)>1.e-9) g[m*N1+n]=p;
if(q>-999 && q<999 && fabs(q)> 1.e-9) f[m*N1+n]=q;
}}
p=2;q=1;
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, (-4.+.1*n),-q, q); fprintf(o,".006 W 0 1 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, (-3.+.1*n),-q, q); fprintf(o,".006 W 0 1 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, (-2.+.1*n),-q, q); fprintf(o,".006 W 0 1 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, (-1.+.1*n),-q, q); fprintf(o,".006 W 0 1 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, ( 0.+.1*n),-q, q); fprintf(o,".006 W 0 1 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, ( 1.+.1*n),-q, q); fprintf(o,".006 W 0 1 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, ( 2.+.1*n),-q, q); fprintf(o,".006 W 0 1 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, ( 3.+.1*n),-q, q); fprintf(o,".006 W 0 1 0 RGB S\n");
//
for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, (-4.+.1*n),-q, q); fprintf(o,".006 W 1 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, (-3.+.1*n),-q, q); fprintf(o,".006 W 1 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, (-2.+.1*n),-q, q); fprintf(o,".006 W 1 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, (-1.+.1*n),-q, q); fprintf(o,".006 W 1 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, ( 0.+.1*n),-q, q); fprintf(o,".006 W 0 0 1 RGB S\n");
for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, ( 1.+.1*n),-q, q); fprintf(o,".006 W 0 0 1 RGB S\n");
for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, ( 2.+.1*n),-q, q); fprintf(o,".006 W 0 0 1 RGB S\n");
for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, ( 3.+.1*n),-q, q); fprintf(o,".006 W 0 0 1 RGB S\n");
//
conto(o,f,w,v,X,Y,M,N, (-24. ),-4*p,4*p); fprintf(o,".020 W 1 0 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (-20. ),-4*p,4*p); fprintf(o,".020 W 1 0 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (-16. ),-4*p,4*p); fprintf(o,".020 W 1 0 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (-12. ),-4*p,4*p); fprintf(o,".020 W 1 0 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (-8. ),-4*p,4*p); fprintf(o,".020 W 1 0 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (-7. ),-p,p); fprintf(o,".020 W 1 0 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (-6. ),-p,p); fprintf(o,".020 W 1 0 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (-5. ),-p,p); fprintf(o,".020 W 1 0 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (-4. ),-p,p); fprintf(o,".020 W 1 0 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (-3. ),-p,p); fprintf(o,".020 W 1 0 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (-2. ),-p,p); fprintf(o,".020 W 1 0 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (-1. ),-p,p); fprintf(o,".020 W 1 0 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, ( 0. ),-8*p,8*p); fprintf(o,".020 W 1 0 1 RGB S\n");
conto(o,f,w,v,X,Y,M,N, ( 1. ),-p,p); fprintf(o,".020 W 0 0 1 RGB S\n");
conto(o,f,w,v,X,Y,M,N, ( 2. ),-p,p); fprintf(o,".020 W 0 0 1 RGB S\n");
conto(o,f,w,v,X,Y,M,N, ( 3. ),-p,p); fprintf(o,".020 W 0 0 1 RGB S\n");
conto(o,f,w,v,X,Y,M,N, ( 4. ),-p,p); fprintf(o,".020 W 0 0 1 RGB S\n");
conto(o,f,w,v,X,Y,M,N, ( 5. ),-p,p); fprintf(o,".020 W 0 0 1 RGB S\n");
conto(o,f,w,v,X,Y,M,N, ( 6. ),-p,p); fprintf(o,".020 W 0 0 1 RGB S\n");
conto(o,f,w,v,X,Y,M,N, ( 7. ),-p,p); fprintf(o,".020 W 0 0 1 RGB S\n");
conto(o,f,w,v,X,Y,M,N, ( 8. ),-4*p,4*p); fprintf(o,".020 W 0 0 1 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (12. ),-4*p,4*p); fprintf(o,".020 W 0 0 1 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (16. ),-4*p,4*p); fprintf(o,".020 W 0 0 1 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (20. ),-4*p,4*p); fprintf(o,".020 W 0 0 1 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (24. ),-4*p,4*p); fprintf(o,".020 W 0 0 1 RGB S\n");
//
conto(o,g,w,v,X,Y,M,N, (-24. ),-4*p,4*p); fprintf(o,".020 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (-20. ),-4*p,4*p); fprintf(o,".020 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (-16. ),-4*p,4*p); fprintf(o,".020 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (-12. ),-4*p,4*p); fprintf(o,".020 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (-8. ),-4*p,4*p); fprintf(o,".020 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (-7. ),-p,p); fprintf(o,".020 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (-6. ),-p,p); fprintf(o,".020 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (-5. ),-p,p); fprintf(o,".020 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (-4. ),-p,p); fprintf(o,".020 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (-3. ),-p,p); fprintf(o,".020 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (-2. ),-p,p); fprintf(o,".020 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (-1. ),-p,p); fprintf(o,".020 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, ( 0. ),-8*p,8*p); fprintf(o,".020 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, ( 1. ),-p,p); fprintf(o,".020 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, ( 2. ),-p,p); fprintf(o,".020 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, ( 3. ),-p,p); fprintf(o,".020 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, ( 4. ),-p,p); fprintf(o,".020 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, ( 5. ),-p,p); fprintf(o,".020 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, ( 6. ),-p,p); fprintf(o,".020 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, ( 7. ),-p,p); fprintf(o,".020 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, ( 8. ),-4*p,4*p); fprintf(o,".020 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (12. ),-4*p,4*p); fprintf(o,".020 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (16. ),-4*p,4*p); fprintf(o,".020 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (20. ),-4*p,4*p); fprintf(o,".020 W 0 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (24. ),-4*p,4*p); fprintf(o,".020 W 0 0 0 RGB S\n");
// #include"plofu.cin"
M(-1,0)L(-8.2,0)
fprintf(o,"0 0 0 RGB 0.05 W [.07 .12] .1 setdash S\n"); fclose(o);
fprintf(o,"showpage\n\%\%\%Trailer"); fclose(o);
//system( "ggv LogFactorialZ.eps"); // for linux
system("open LogFactorialZ.eps"); //for macintosh
system("ps2pdf LogFactorialZ.eps");
getchar(); system("killall Preview");//for macintosh
}
// End of generator of figure http://en.citizendium.org/wiki/Image:LogFactorialZ.jpg