Bessel functions: Difference between revisions
imported>David Binner No edit summary |
imported>Dmitrii Kouznetsov (add complex map of J_0) |
||
| (26 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
{{subpages}} | {{subpages}} | ||
Bessel functions are solutions of the Bessel differential equation: | [[File:Besselj0j1plotT.png|400px|thumb|Explicit plots of the <math>J_0</math> and <math>J_1</math> from <ref name="toriplot"> | ||
http://tori.ils.uec.ac.jp/TORI/index.php/File:Besselj0j1plotT.png | |||
Explicit plots of the <math>J_0</math> and <math>J_1</math>. | |||
</ref>]] | |||
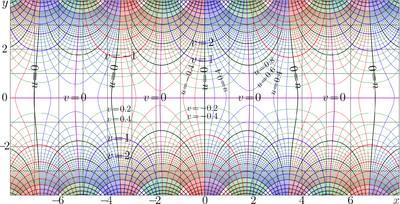
[[File:Besselj1mapT080.png|400px|thumb|[[Complex map]] of <math>J_1</math> by | |||
<ref name="torimapj0"> | |||
http://tori.ils.uec.ac.jp/TORI/index.php/File:Besselj1map1T080.png | |||
Complex map of the Bessel function BesselJ1. | |||
</ref>; | |||
<math>u+\mathrm i v = J_1(x+\mathrm i y)</math> | |||
]]. | |||
'''Bessel functions''' are solutions of the Bessel differential equation:<ref>{{cite book|author=Frank Bowman|title=Introduction to Bessel Functions|edition=1st Edition|publisher=Dover Publications|year=1958|id=ISBN 0-486-60462-4}}</ref><ref>{{cite book|author=George Neville Watson|title=A Treatise on the Theory of Bessel Functions|edition=2nd Edition|publisher=Cambridge University Press|year=1966|id=}}</ref><ref>[http://mathworld.wolfram.com/BesselFunctionoftheFirstKind.html Bessel Function of the First Kind] Eric W. Weisstein, From the website of "MathWorld--A Wolfram Web Resource".</ref> | |||
:<math> z^2 \frac | :<math> z^2 \frac {d^2 w}{dz^2} + z \frac {dw}{dz} + (z^2 - \alpha^2)w = 0 </math> | ||
where α is a constant. | where α is a constant. | ||
| Line 13: | Line 24: | ||
In addition, a linear combination of these solutions is also a solution: | In addition, a linear combination of these solutions is also a solution: | ||
(iii) H<sub>α</sub> = C<sub>1</sub> J<sub>α</sub>(x) + C<sub>2</sub> Y<sub>α</sub>(x) | (iii) H<sub>α</sub>(x) = C<sub>1</sub> J<sub>α</sub>(x) + C<sub>2</sub> Y<sub>α</sub>(x) | ||
where C<sub>1</sub> and C<sub>2</sub> are constants. | where C<sub>1</sub> and C<sub>2</sub> are constants. | ||
| Line 19: | Line 30: | ||
These three kinds of solutions are called Bessel functions of the first kind, second kind, and third kind. | These three kinds of solutions are called Bessel functions of the first kind, second kind, and third kind. | ||
== | ==Properties== | ||
Many properties of functions $J$, $Y$ and $H$ are collected at the handbook by [[Abramowitz, Stegun]] | |||
<ref> | |||
http://people.math.sfu.ca/~cbm/aands/page_358.htm | |||
M. Abramowitz and I. A. Stegun. | |||
Handbook of mathematical functions. | |||
</ref>. | |||
===Integral representations=== | |||
: <math> \!\!\!\!\!\!\!\!\!\! (9.1.20) ~ ~ ~ \displaystyle | |||
J_\nu(z) = \frac{(z/2)^{\nu}}{\pi^{1/2} ~(\nu-1/2)!} | |||
~ | |||
\int_0^\pi | |||
~ | |||
\cos(z \cos(t)) \sin(t)^{2 \nu} ~t~ \mathrm d t | |||
</math> | |||
===Expansions at small argument=== | |||
: <math>\displaystyle J_\alpha(z) | |||
=\left(\frac{z}{2}\right)^{\!\alpha} ~ | |||
\sum_{k=0}^{\infty} | |||
~ \frac{ (-z^2/4)^k}{ k! ~ (\alpha\!+\!k)!} | |||
</math> | |||
The series converges in the whole complex $z$ plane, but fails at negative integer values of <math>\alpha</math> . The postfix form of [[factorial]] is used above; <math>k!=\mathrm{Factorial}(k)</math>. | |||
==Applications== | |||
Bessel functions arise in many applications. For example, [[Johannes Kepler|Kepler]]’s [[Kepler's laws|Equation of Elliptical Motion]], the vibrations of a membrane, and heat conduction, to name a few. | |||
In [[paraxial optics]] the Bessel functions are used to describe solutions with circular symmetry. | |||
==References== | |||
{{reflist}} | |||
Latest revision as of 07:58, 13 July 2012
.
Bessel functions are solutions of the Bessel differential equation:[3][4][5]
where α is a constant.
Because this is a second-order differential equation, it should have two linearly-independent solutions:
(i) Jα(x) and
(ii) Yα(x).
In addition, a linear combination of these solutions is also a solution:
(iii) Hα(x) = C1 Jα(x) + C2 Yα(x)
where C1 and C2 are constants.
These three kinds of solutions are called Bessel functions of the first kind, second kind, and third kind.
Properties
Many properties of functions $J$, $Y$ and $H$ are collected at the handbook by Abramowitz, Stegun [6].
Integral representations
Expansions at small argument
The series converges in the whole complex $z$ plane, but fails at negative integer values of . The postfix form of factorial is used above; .
Applications
Bessel functions arise in many applications. For example, Kepler’s Equation of Elliptical Motion, the vibrations of a membrane, and heat conduction, to name a few. In paraxial optics the Bessel functions are used to describe solutions with circular symmetry.
References
- ↑ http://tori.ils.uec.ac.jp/TORI/index.php/File:Besselj0j1plotT.png Explicit plots of the and .
- ↑ http://tori.ils.uec.ac.jp/TORI/index.php/File:Besselj1map1T080.png Complex map of the Bessel function BesselJ1.
- ↑ Frank Bowman (1958). Introduction to Bessel Functions, 1st Edition. Dover Publications. ISBN 0-486-60462-4.
- ↑ George Neville Watson (1966). A Treatise on the Theory of Bessel Functions, 2nd Edition. Cambridge University Press.
- ↑ Bessel Function of the First Kind Eric W. Weisstein, From the website of "MathWorld--A Wolfram Web Resource".
- ↑ http://people.math.sfu.ca/~cbm/aands/page_358.htm M. Abramowitz and I. A. Stegun. Handbook of mathematical functions.