Second law of thermodynamics

The second law of thermodynamics, as formulated in the middle of the 19th century by William Thomson (Lord Kelvin) and Rudolf Clausius, states that it is impossible to gain mechanical energy (work) from heat flowing from a cold to a hot body. Clausius postulated that the opposite is the case: it requires input of mechanical (or electric) energy to transport heat from a low- to a high-temperature object. A heat pump, air conditioner, and refrigerator are devices that move heat from a cold to a warm place: according to Clausius they need mechanical or electric energy (work) to do it.

Thomson formulated the second law in a slightly different, but equivalent way. He used the concept of heat engine. This is a virtual machine that converts heat into work while operating according to thermodynamic rules. Thomson postulated that it is impossible for a cyclic heat engine to receive its input from a single heat source. In a cyclic thermodynamic process, a system—such as a heat engine—ends up in a thermodynamic state that is the same as the initial state; the system has not lost or gained any internal energy after a full cycle. In order that no energy is lost in the supersystem heat-source-plus-heat-engine after a full cycle, it is necessary that the work generated by the engine is converted into heat that is returned to the heat source. According to Thomson, a heat reservoir cannot play the same role as a bank that lends money to a customer. It is not possible for a heat engine to "loan" an amount of heat from a single heat source, get work out of it, and bring back the "loaned" heat later to the same source.

Discussion of the second law

If the second law would not hold, there would be no fear of energy shortage. For example, it would be possible—as already pointed out by Lord Kelvin—to propel ships by energy extracted from sea water. After all, the oceans contain immense amounts of internal energy. When one could extract just a small portion of it—whereby a slight cooling of the sea water would occur—and use this to propel a ship (a form of work), then ships could move without any net consumption of energy. It would not violate the first law of thermodynamics, because the rotation of the ship's propellers would again heat the water and in total the energy of the supersystem "ship-plus-ocean" would be conserved, in agreement with the first law. Unfortunately, it is not possible, no work can be extracted from the water because it would be a single source of heat. Clausius would explain the violation of the law by observing that ships are warmer than sea water (or at least they are not colder) and hence it needs work to transport heat from the sea to the ship.

PD Image
Fig. 1. T_h > T_c. Second law (Kelvin): if W > 0, Q_c ≠ 0.

Without the second law, one could conceive a similar setup on land where energy, extracted from the earth, would charge batteries, and heat, dissipated by electric currents generated by the batteries, would be given back to the earth. Such a device is also out of the question because the second law forbids it.

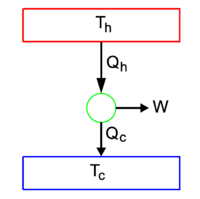
The second law is summarized in the figure 1. Two heat reservoirs are shown, one of absolute temperature T_h (the hot reservoir) and the other of temperature T_c (the cold reservoir), T_h >T_c. The reservoirs are coupled by a heat engine (green circle), a construct that converts heat Q_h into work W. The "rest heat" Q_c is delivered to the cold reservoir. This idealized representation of power-generating machines was invented by Sadi Carnot who used it for the study of steam engines. But this schematic representation applies to many machines, for instance also to an automobile, a vehicle with an internal combustion engine. The high-temperature heat bath is formed by the cylinders which are hot because of the combustion of gasoline. The cold heat bath is formed by the environment of the car—the rest heat is delivered to the surroundings through the car's radiator. The cyclically moving pistons, that perform the actual work, form the heat engine.

An essential feature of the process depicted in figure 1 is that it is reversible: all arrows may be reverted, in which case figure 1 represents heat flowing from cold to hot and according to Clausius work must be done by the surroundings on the system (represented by an inward arrow).

When the heat flow is from hot to cold, work W is performed by the engine on the surroundings (outgoing W in figure 1). The Kelvin principle states that Q_c ≠ 0, because otherwise there would be a single heat source delivering the work. Hence, the second law states that only part of the heat Q_h obtained from the hot reservoir, can be converted into work, the remaining part of Q_h is given off as the non-zero rest heat Q_c to the low temperature reservoir. [In the case of a car it means that only part of the combustion energy is converted into work and that the other part of the combustion energy heats up the air surrounding the car.]

It can be shown that the efficiency η ≡ W / Q_h is bounded:

$\eta \leq {\frac {T_{\mathrm {h} }-T_{\mathrm {c} }}{T_{\mathrm {h} }}}$

Thus, when car cylinders operate at, say, 427 °C = 700 K and the surroundings are 27 °C = 300 K, then η ≤ 400/700 = 57%. This percentage is used for driving the car, the other 43% is lost to the surroundings. It is important to note that the efficiency is limited by the second law of thermodynamics; η can only be raised by higher T_h, not by a better streamline of the car or other design improvements.

Mathematical expression of the second law

We consider a single thermodynamic system of absolute temperature T, and let DQ be a small amount of heat entering the system. In the article entropy it is proved from the Clausius/Kelvin principle that a thermodynamic system is characterized, not only by its usual parameters volume, pressure, etc., but also by the state variable S, the entropy of the system. The differential dS is defined by

$dS\;{\stackrel {\mathrm {def} }{=}}\;{\frac {DQ}{T}}>0.$

When DQ leaves the system,

$dS\equiv -{\frac {DQ}{T}}<0.$

Reversible processes

The fact that entropy S is a state function implies that the following holds for a reversible cyclic process,

$\oint {\frac {DQ}{T}}\equiv {\int \limits _{1}\limits ^{2}}_{{\!\!}^{(I)}}{\frac {DQ}{T}}+{\int \limits _{2}\limits ^{1}}_{{\!\!}^{(II)}}{\frac {DQ}{T}}=\oint dS=0.$

This equation is the mathematical expression of the second law of thermodynamics for the special case of reversible processes. The cycle consists of two different paths in state space, denoted by I and II. The path integrals start and end at common points in state space, indicated by 1 and 2.

In order to show conversely that this equation yields the Clausius principle, we consider the heat engine (green circle) in figure 1 as our system and assume that both heat baths are so large (or the engine so small) that one full cycle of the engine does not change the temperatures of the baths. Then for one cycle of the engine one can write,

$\oint dS=\oint {\frac {DQ_{\mathrm {h} }}{T_{\mathrm {h} }}}-\oint {\frac {DQ_{\mathrm {c} }}{T_{\mathrm {c} }}}={\frac {Q_{\mathrm {h} }}{T_{\mathrm {h} }}}-{\frac {Q_{\mathrm {c} }}{T_{\mathrm {c} }}}=0\quad \qquad \qquad (1)$

where we defined

${\frac {Q_{\mathrm {h} }}{T_{\mathrm {h} }}}\equiv \oint {\frac {DQ_{\mathrm {h} }}{T_{\mathrm {h} }}}={\frac {1}{T_{\mathrm {h} }}}\oint DQ_{\mathrm {h} },$

and the analogous definition holds for Q_c. Note that from the reverse process (heat flowing from cold to hot) one obtains the same result.

By definition Q_h and Q_c are positive amounts of heat. With regard to the work W, one must carefully distinguish whether work is performed by (W_by) or on (W_on) the system. Clearly W_by = −W_on. Observe further that from equation (1) it follows that

${\frac {Q_{\mathrm {h} }}{Q_{\mathrm {c} }}}={\frac {T_{\mathrm {h} }}{T_{\mathrm {c} }}}>1,\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad (2)$

i.e., Q_h > Q_c irrespective of the direction of the heat flow.

When the heat flow is from hot to cold (arrows are as shown in figure 1), the first law states that work by the system (outward arrow) obeys the equation

$W_{\mathrm {by} }=Q_{\mathrm {h} }-Q_{\mathrm {c} }>0,\,\quad \qquad \qquad \qquad \qquad \qquad \qquad \qquad (3)$

that is, the heat engine performs work on its surroundings.

When the heat flow is from cold to hot (all arrows are reverted in figure 1), the first law of thermodynamics states that work on the system (inward arrow) is

$W_{\mathrm {on} }=Q_{\mathrm {h} }-Q_{\mathrm {c} }>0,\,$

meaning that the surroundings perform work on the heat engine. Hence, from the mathematical formulation of the second law follows, in correspondence with the Clausius principle, that work on the system is needed to transport heat from the cold to the hot reservoir.

The efficiency η follows from equations (2) and (3)

$\eta \equiv {\frac {W_{\mathrm {by} }}{Q_{\mathrm {h} }}}={\frac {Q_{\mathrm {h} }-Q_{\mathrm {c} }}{Q_{\mathrm {h} }}}=1-{\frac {Q_{\mathrm {c} }}{Q_{\mathrm {h} }}}=1-{\frac {T_{\mathrm {c} }}{T_{\mathrm {h} }}}={\frac {T_{\mathrm {h} }-T_{\mathrm {c} }}{T_{\mathrm {h} }}},$

and since T_h > T_c > 0, it follows that η < 1.

It is good to stress that the inequality η < 1 holds for reversible processes in which there are no entropy losses. Often the fact that η is less than unity is given in the very same discussion as in which it is pointed out that entropy strives toward a maximum. It is then easy to draw the incorrect conclusion that η being less than one is solely due to entropy losses. It is true, however, that in spontaneous (irreversible) processes the entropy does increase with the consequence that the efficiency η is further reduced; the equation for η becomes an upper bound. That is, for irreversible processes the equality that is valid for reversible processes, becomes an inequality,

$\eta <{\frac {T_{\mathrm {h} }-T_{\mathrm {c} }}{T_{\mathrm {h} }}}.$

Spontaneous, irreversible, processes

PD Image
Fig. 2. Upper (red) vessel contains hot fluid, lower (blue) vessel cold. The vessels have heat-conducting walls and are in a container with adiabatic walls (black).

Many, in fact most, thermodynamic processes are spontaneous and irreversible. A well-known spontaneous process is the flow of heat from a vessel containing hot fluid to one containing cold fluid, see figure 2. The opposite process, the transport of heat from a cold to a hot vessel, needs work by the Clausius principle and is accordingly not spontaneous. The spontaneous flow of heat from hot to cold is irreversible; the terms "spontaneous" and "irreversible" will be used interchangeably in what follows.

Another example of an irreversible process is Count Rumford's seminal cannon boring experiment in which work by a drill is converted into frictional heat. This process cannot be reverted because of the Kelvin principle. It is impossible to obtain work from the frictional heat without another, colder, reservoir present. The cannon-plus-drill forms a single source of heat.

The Joule-Thomson effect shows yet another example of an irreversible process.

In figure 2 it is shown that during a certain short time span a small amount of heat DQ flows from the upper to the lower vessel, T_h > T_c. For the loss and gain of an infinitesimal amount of heat we may use the equations for the change in entropy given in the previous section. That is, the upper (hot) container loses entropy, while the lower (cold) gains entropy. For the total isolated system it holds that

$dS=-{\frac {DQ}{T_{\mathrm {h} }}}+{\frac {DQ}{T_{\mathrm {c} }}}=DQ\left({\frac {1}{T_{\mathrm {c} }}}-{\frac {1}{T_{\mathrm {h} }}}\right)>0.$

Clearly, heat will keep on flowing until the temperature of both vessels has become equal and the entropy of the isolated system has increased and finally S₂ − S₁ > 0. If the same amount of heat had been transferred from the hot to the cold reservoir, but reversibly through a heat engine, as in figure 1, work would have been delivered by the heat flow, while the spontaneous process of figure 2 does not perform any work. This already shows that a spontaneous process yields less work than the corresponding reversible process. This, in turn, means that the efficiency η of a spontaneous process is smaller than the efficiency of the corresponding reversible process, a result that was preluded above.

PD Image
Fig. 3. Reversible (full) and irreversible (dashed) path in state space of the closed system C are depicted inside C. E is a reversible heat engine and R an infinite heat reservoir.

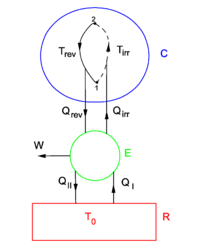
In order to give the formulation of the second law of thermodynamics for irreversible processes of arbitrary systems, we consider figure 3. A system consisting of a closed system C (only heat goes in and out) and a reversible heat engine E is coupled to a large heat reservoir R of constant temperature T₀. The system C undergoes a cyclic state change, where from 1 to 2 the change is irreversible (dashed line) and from 2 to 1 it is reversible (full line). Since the change 1–2–1 is a cycle and no work is performed on or by C, it follows that

$Q_{\mathrm {rev} }=Q_{\mathrm {irr} }\quad {\hbox{with}}\quad Q_{\mathrm {rev} }\equiv \int _{1}^{2}DQ_{\mathrm {rev} },\quad Q_{\mathrm {irr} }\equiv \int _{1}^{2}DQ_{\mathrm {irr} }.$

For the heat engine E it holds that

${\frac {DQ_{\mathrm {rev} }}{DQ_{\mathrm {II} }}}={\frac {T_{\mathrm {rev} }}{T_{0}}}\quad {\hbox{and}}\quad {\frac {DQ_{\mathrm {irr} }}{DQ_{\mathrm {I} }}}={\frac {T_{\mathrm {irr} }}{T_{0}}}$

Hence

${\frac {Q_{\mathrm {II} }}{T_{0}}}\equiv {\frac {1}{T_{0}}}\int _{1}^{2}DQ_{\mathrm {II} }=\int _{1}^{2}{\frac {DQ_{\mathrm {rev} }}{T_{\mathrm {rev} }}}\quad {\hbox{and}}\quad {\frac {Q_{\mathrm {I} }}{T_{0}}}\equiv {\frac {1}{T_{0}}}\int _{1}^{2}DQ_{\mathrm {I} }=\int _{1}^{2}{\frac {DQ_{\mathrm {irr} }}{T_{\mathrm {irr} }}}.$

From Kelvin's principle it follows that W < 0, because there is only the single heat source R. Invoking the first law of thermodynamics one obtains,

$W=Q_{\mathrm {I} }-Q_{\mathrm {II} }<0\;\Longrightarrow \;{\frac {Q_{\mathrm {II} }}{T_{0}}}>{\frac {Q_{\mathrm {I} }}{T_{0}}},$

so that

$\int _{1}^{2}{\frac {DQ_{\mathrm {rev} }}{T_{\mathrm {rev} }}}>\int _{1}^{2}{\frac {DQ_{\mathrm {irr} }}{T_{\mathrm {irr} }}}$

Since the path 2 to 1 is reversible, the left-hand side of this inequality is equal S₂−S₁ and the final result becomes

$S_{2}-S_{1}>\int _{1}^{2}{\frac {DQ_{\mathrm {irr} }}{T_{\mathrm {irr} }}}\Longleftrightarrow dS>{\frac {DQ_{\mathrm {irr} }}{T_{\mathrm {irr} }}},$

which proves the second law of thermodynamics for irreversible processes from the Kelvin principle.

References

• J. de Boer in Textbook of physics, Pergamon Press London, New York (1959). Editor R. Kronig. (English translation from the Dutch Leerboek der Natuurkunde)
• C. S. Helrich, Modern Thermodynamics with Statistical Mechanics, Springer (2009).