In analytic geometry, a reflection is a linear operation σ on  with σ2 = 1, i.e., σ is an involution, and
σ−1 = σ. Reflecting twice an arbitrary vector brings back the original vector :
with σ2 = 1, i.e., σ is an involution, and
σ−1 = σ. Reflecting twice an arbitrary vector brings back the original vector :

The operation σ is orthogonal, i.e., preserves inner products, so that

Reflection is orthogonal and symmetric.
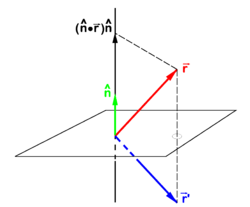
PD Image Fig. 1. The vector

goes to

under reflection in a plane. The unit vector

is normal to mirror plane.
Reflection in a plane
If  is a unit vector normal (perpendicular) to a plane—the mirror plane—then
is a unit vector normal (perpendicular) to a plane—the mirror plane—then  is the projection of
is the projection of  on this unit vector. From the figure it is evident that
on this unit vector. From the figure it is evident that

If a non-unit normal  is used then substitution of
is used then substitution of

gives the mirror image,

This relation can be immediately generalized to m-dimensional inner product spaces. Let the space Vm allow an orthogonal direct sum decomposition into a 1-dimensional and a (m−1)-dimensional subspace,

and let v be an element of the one-dimensional space V1 then the involution

is a reflection of r in the hyperplane Vm−1. (By definition a hyperplane is an m−1-dimensional linear subspace of a linear space of dimension m.) The inner product of two vectors v and w is notated as (v, w), which is common for vector spaces of arbitrary dimension.
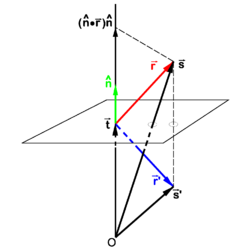
PD Image Fig. 2. The vector

goes to

under reflection
Reflection in plane not through origin
In Figure 2 a plane, not containing the origin O, is considered that is orthogonal to the vector  . The length of this vector is the distance from O to the plane.
From Figure 2, we find
. The length of this vector is the distance from O to the plane.
From Figure 2, we find

Use of the equation derived earlier gives

And hence the equation for the reflected pair of vectors is,

where  is a unit normal to the plane. Obviously
is a unit normal to the plane. Obviously  and
and  are proportional, differ by a scaling.
are proportional, differ by a scaling.
Two consecutive reflections
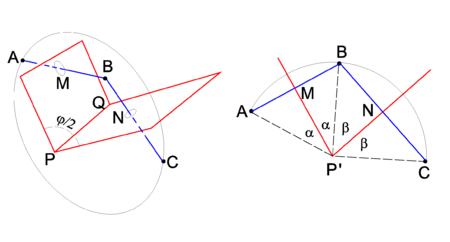
PD Image Fig. 3. Two reflections. Left drawing: 3-dimensional drawing. Right drawing: view along the PQ axis, drawing projected on the plane through ABC. This plane intersect the line PQ in the point P′
Two consecutive reflections in two intersecting planes give a rotation around the line of intersection. This is shown in Figure 2, where PQ is the line of intersection.
The drawing on the left shows that reflection of point A in the plane through PMQ brings the point A to B. A consecutive reflection in the plane through PNQ brings B to the final position C. In the right-hand drawing it is shown that the rotation angle φ is equal to twice the angle between the mirror planes. Indeed, the angle ∠ AP'M = ∠ MP'B = α and ∠ BP'N = ∠ NP'C = β. The rotation angle ∠ AP'C ≡ φ = 2α + 2β and the angle between the planes is α+β = φ/2.
From the point of view of matrices this result follows easily also. A reflection is represented by an improper matrix, that is, by an orthogonal matrix with determinant −1. The product of two orthogonal matrices is again an orthogonal matrix and the rule for determinants is det(AB) = det(A)det(B), so that the product of two improper rotation matrices is an orthogonal matrix with unit determinant, i.e., the matrix of a proper rotation.























