< User talk:Paul WormerRevision as of 05:06, 30 March 2010 by imported>Paul Wormer
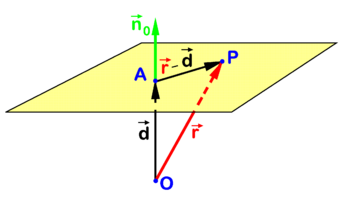
PD Image Equation for plane. X is arbitary point in plane;  and
and  are collinear.
are collinear. In analytic geometry several closely related algebraic equations are known for a plane in three-dimensional Euclidean space. One such equation is illustrated in the figure. Point X is an arbitrary point in the plane and O (the origin) is outside the plane. The point A in the plane is chosen such that vector

is orthogonal to the plane. The collinear vector

is a unit (length 1) vector normal (perpendicular) to the plane. Evidently a is the distance of O to the plane. The following relation holds for an arbitrary point X in the plane

This equation for the plane can be rewritten in terms of coordinates with respect to a Cartesian frame with origin in O. Dropping arrows and hat for component vectors (real triples), we find

with

Conversely, given the following equation for a plane

writing

it follows that

Hence

where f , a, and n are collinear.











