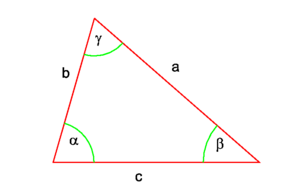
Sine rule
In trigonometry, the sine rule (also known as Law of Sines) states that the ratio of the sines of the angles of a triangle is equal to the ratio of the lengths of the opposite sides, see Fig.1. Equivalently,
where d is the diameter of the circle circumscribing the triangle.
Proof
The easiest proof is purely geometric.
Lemma
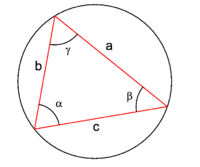
In Fig. 2 the arbitrary angle α' satisfies,
where d is the diameter of the circle and a is the chord opposite α'. This follows because the two angles, α and α', in Fig. 2 share a segment of the circle (have the chord a in common). By a well-known theorem of plane geometry it follows that the two angles are equal. The angle α, having the diameter of the circle d as one of its sides, has as opposite angle a right angle. Hence sin(α) = a/d, the length of chord a divided by the diameter d. It follows that the angle α' has the same sine as α.
Proof of sine rule
From the lemma follows that the angles in Fig. 3 are
where d is the diameter of the circle. From this result the sine rule follows.