User:Dmitrii Kouznetsov/Analytic Tetration

Fig.0. Graphic of analytic tetration $f={\rm {sex}}_{2}(x)=\exp _{2}^{x}(1)$ at versus $x$.

Analytic tetration

by Dmitrii Kouznetsov.

Template:Under construction

Abstract

Analytic tetration is defined as mathematical function that coincides witht the tetration at integer values of the argument and is analytic outside the negative part of the real axis. Existence of such a function is postulated; and arguments in favor of uniqueness of such a function are considered. The algorithm of evaluation is suggested. Examples of evaluation, pictures and tables are supplied. The application and the generalization is discussed.

Preface

The colleagues indicated so many misprints in my papers about tetration, posted at my homepage , that I want to give them opportunity to correct them in real time.

I consider the topic very important and urgent. The analytic tetration should be investigated and discussed right now; overvice, the non-analytic extension may become an ugly standard in mathematics of computation; the implementation of hige numbers with non-analycit tetration would make difficult realization of arithmetic operations and cause a lot of incompatibilities.

This is my apology for posting this research now, while the rigorous proof of existence and uniqueness of the analytic tetration is not yet found. My believe is based on the numerical check of the hypothesis of the existence and uniqueness, on smallness of the residual at the substitution of the function to the tetration equation and beauty of the resulting pictures. I cannot imagine that the agreement with 14 decimal digits occurs just by occasion without deep mathematical meaning.

In such a way I apologize for postulating of statements which should be prooven by the rigorous mathematical deduction.

Introduction

Quick start

Roughly, super-exponential

(1) ${\rm {sex}}_{b}(z)=\exp _{b}^{z}(1)$

is combination of $x$ exponentials on base $b$. Foe example,

$~{\rm {sex}}_{b}(0)=\exp _{b}^{0}(1)=1$

$~{\rm {sex}}_{b}(1)=\exp _{b}(1)=b$

$~{\rm {sex}}_{b}(2)=\exp _{b}^{2}(1)=\exp _{b}(\exp _{b}(1))=b^{b}$

$~{\rm {sex}}_{b}(3)=\exp _{b}^{3}(1)=\exp _{b}{\Big (}\exp _{b}{\big (}\exp _{b}(1){\big )}{\Big )}=b^{b^{b}}$

and so on. However, such definition is good only for positive integer values of $x$. In general, the superexponential can be defined through the Abel equation

(2) $~\exp _{b}{\Big (}{\rm {sex_{b}}}(z){\Big )}={\rm {sex}}_{b}(z+1)$

with assitional condition that

(3) $~{\rm {sex_{b}}}(0)=1$

Then, at least for positive values of $~b$ and positive integer values of $~z$, such a definition can be used for the evaluation of tetration.

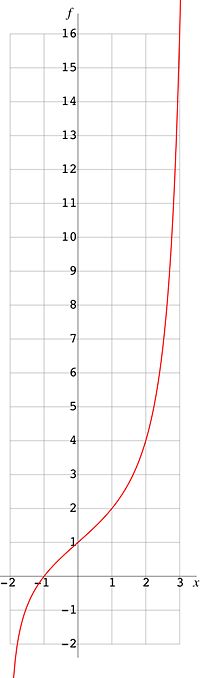
In this paper, the way to define tetration for non-integer argument is described. For real values of the argument, at $~b=2$, such a tetration is plotted on figure 0. In the following sections, I describe, why is it so important, how to define the tetration for non-integer values of the argument, how can it be evaluated with high precision and why it is the only correct way to define analytic tetration.

Additional argument

One can consider to add the additional argument, replacing $~\exp _{b}(1)$ to $~\exp _{b}(a)$. This may have sense, while $~z$ is allowed to have only integer values. However, at the implementation of "good" tetration, the "argument" $~a$ can be considered as inverse superexponential of some argument, $~a={\rm {sex}}_{b}(\alpha )$; then, $~\exp _{b}^{z}(a)={\rm {sex}}_{b}{\Big (}{\rm {sex}}_{b}(\alpha ){\Big )}$; in the way, similar to that of convential logarithms: it is sufficient to investigate properties of natural logarithm ln; then, any other can be expressed as $\log _{b}(z)=\ln(z)/\ln(b)$.

$\exp _{b}^{n}(\exp _{b}^{m}(z))=\exp _{b}^{m+n}(z)$

The exponentiation of tetration is equivalent to increment of its argument. While summaton operation forms the group, exponentiation does too.

$\exp _{b}^{m}({\rm {sex}}_{b}(z))={\rm {sex}}_{b}(z+m)$

Inverse function and group properties

In this section, I write $~F$ instead of $~{\rm {sex}}_{b}$ and $~\exp(z)$ instead of $~\exp _{b}(z)$; onitting indices. However, you may recover them at any moment.

(I am not sure which notation is best. D.)

The speculation of the previous subseciton can be written shorter.

Assume there exist function $~F^{-1}$ such that $~F{\Big (}F^{-1}(z){\Big )}=z$.

Let $~s=\exp ^{u}(t)=F{\Big (}u+F^{-1}(t){\big )}$ and $~q=\exp ^{v}(s)=F{\Big (}v+F^{-1}(s){\big )}$ .

Then $~q=\exp ^{v}{\Big (}\exp ^{u}(t){\Big )}=F{\Big (}v+F^{-1}{\Big (}F(u+F^{-1}(t)){\Big )}{\Big )}=F{\Big (}v+u+F^{-1}(t){\Big )}$.

You can put subscript $~_{b}$ to $~F$ and $~\exp$ in the defuction above, and it will be seen, that we have no need to deal with funciton of 2 variables, considering $\exp _{b}^{z}(x)$; it can be expressed in terms of $F_{b}(z)$. However, we need to specify, what set shold be $~t$ and Failed to parse (syntax error): {\displaystyle ~s<math> from in the deduction above: mist they be positive integer, or they can be real, of they can be also complex numbers. ==History of tetration and huge numbers== Perhaps, every researcher used to see diagnostivs "floating overflow" at the evlauation of an expression with huge numbers.... ===[[Ackermann functions]]=== ===Ambiguity of the real-analytic extension=== ==Asymptotic== ===Variety of tertations=== ===Eigenvalues of logarithm=== [[Image:ExampleEquationLog01.png|300px|right|thumb|FIg.1. Example of graphic solution of equation <math>L=\log_b(L)} for $b={\sqrt {2}}$ (two real solutions, $L=2$ and $L=4$), $b=\exp(1/{\rm {e)}}$ (one real solution $L={\rm {e}}$) $b=2$ (no real solutions).]]

I search for the simplest solution, that asymptotically, approaches the eigenvalue of logarithm. For $b$ slightly larger than unity, there exist real sloutions, as it is shown in figure 1.

FIg.2. parameters of asymptotic of tetration versus logarithm of the base

For $b>\exp(1/{\rm {e)}}$, there are 2 complex solutions shown in figure 2.