User:Aleksander Stos/ComplexNumberAdvanced

This is an experimental draft. For a brief description of this project click here.

Definition

Complex numbers are defined as ordered pairs of reals:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{C}= \{ (a,b) \colon a,b\in \mathbb{R} \}.}

Such pairs can be added and multiplied as follows

• addition: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (a, b) + (c, d) = (a + c, b + d)}
• multiplication: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (a, b)(c, d) = (ac - bd, bc + ad)}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle \mathbb{C}} with the addition and multiplication is the field of complex numbers. From another of view, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle \mathbb{C} } with complex additions and multiplication by real numbers is a 2-dimesional vector space.

To perform basic computations it is convenient to identify numbers of the form Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{ (a,0):\;\;a\in\mathbb{R} \}} and to introduce the imaginary unit, i=(0,1). The imaginary unit has the property Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle i^2=-1.} Indeed, $(0,1)\cdot(0,1) = (-1,0) = -1.</math> Any complex number Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=(a,b)} can be written as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=a+bi} (this is often called the algebraic form) and vice-versa. The numbers a and b are called the real part and the imaginary part of z, respectively. We denote Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a=\Re (z)} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b=\Im (z).} Remark that two complex numbers are equal if and only if their real and complex part are equal, respectively. Notice that i makes the multiplication quite natural:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (a + bi)(c + di) = (ac - bd) + (bc + ad)i. }

The square root of number in the denominator in the above formula is called the modulus of z and denoted by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |z|} ,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |z|=\sqrt{a^2+b^2}.}

We have for any two complex numbers Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_1} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_2}

• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\bar z| = |z|;}
• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |z_1\cdot z_2| = |z_1| \cdot |z_2|;}
• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |\frac{z_1}{ z_2}| = \frac{|z_1|}{|z_2|},} provided Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_2\not =0.}
• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \big| |z_1| - |z_2| \big| \le |z_1+z_2| \le |z_1| + |z_2|}

For Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=a+bi} we define also Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bar z} , the conjugate, by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bar z= a-bi.} Then we have

• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bar{(\bar z)} = z}
• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bar z_1 \pm \bar z_2 = \overline{(z_1 \pm z_2)};}
• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bar z_1 \cdot \bar z_2 = \overline{(z_1\cdot z_2)};}
• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overline{\left( \frac{z_1}{z_2} \right)} = \frac{\bar z_1}{\bar z_2},} provided Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_2\not =0;}
• Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z\bar z = |z|^2.}

Geometric interpretation

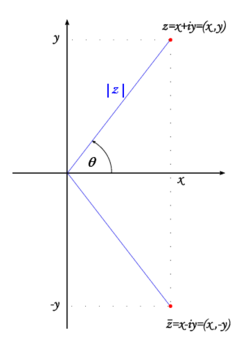
Complex numbers may be naturally represented on the complex plane, where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=x+iy} corresponds to the point (x,y), see the fig. 1.

Fig. 1. Graphical representation of a complex number and its conjugate

The modulus is just the distance from the point Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=(x,y)} and the origin. More generally, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |z_1-z_2|} is the distance between the two given points. Furthermore, the conjugation is just the symmetry with respect to the x-axis.

Trigonometric and exponential form

As the graphical representation suggests, any complex number z=a+bi of modulus 1 (i.e. a point from the unit circle) can be written as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=\cos \theta + i\sin\theta} for some Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta\in [0,2\pi).} So actually any (non-null) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z\in\mathbb{C}} can be represented as

$z=r(\cos \theta +i\sin \theta ),$ where r traditionally stands for |z|.

This is the trigonometric form of the complex number z. If we adopt convention that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta \in [0,2\pi)} then such Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} is unique and called the argument of z. The equality of two complex numbers Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_1=r_1e^{i\theta_1}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_2=r_2e^{i\theta_2}} is equivalent to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r_1=r_2} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_1=\theta_2+2k\pi} for certain integer k. Graphically, the number Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} is the (oriented) angle between the x-axis and the interval containing 0 and z. Closely related is the exponential notation. If we define complex exponential as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^z = \sum_0^\infty \frac{z^n}{n!},}

then it may be shown that

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{i\theta}=\cos\theta + i\sin\theta,\quad\quad \theta\in\mathbb{R}. }

Consequently, any (non-zero) Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z\in \mathbb{C}} can be written as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z= r e^{i\theta}} with the same r and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle theta} as above.

This is called the exponential form of the complex number z. It is well-adapted to perform multiplications. Indeed, for any Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_1=r_1e^{i\theta_1}} and $z_{2}=r_{2}e^{i\theta _{2}}$ we have

• $z_{1}z_{2}=r_{1}r_{2}e^{i(\theta _{1}+\theta _{2})}$
• ${\frac {z_{1}}{z_{2}}}={\frac {r_{1}}{r_{2}}}e^{i(\theta _{1}-\theta _{2})},$ provided $z_{2}\not =0.$

The following particular case of complex multiplication is well-know as the de Moivre's formula

$(cos\theta +i\sin \theta )^{n}=\cos(n\theta )+i\sin(n\theta )$

Fig 2. Multiplication by $i$ amounts to rotation by 90 degrees.

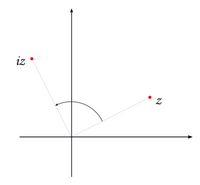
Graphically, multiplication by a constant complex number $z=re^{i\theta }$ amounts to the rotation by $\theta$ and the homothety of ratio r. In particular, the multiplication by i amounts to the rotation by the right angle (counter-clockwise), see Fig. 2.

Complex roots

Any non-constant polynomial with complex coefficients has a complex root. This result is known as the Fundamental Theorem of Algebra. Consequently, any complex polynomial of degree n has exactly n roots (counted with multiplicities). In particular, the equation

$z^{n}=a$,

where z is the variable and a a non-zero constant has exactly n solutions. They are called n^th (complex) roots of a. If a is written in the exponential form, $a=re^{i\theta },$ then the n roots of a, denoted as $z_{0},z_{2},\ldots ,z_{n-1}$, are given by

$z_{k}={\sqrt[{n}]{r}}\cdot \exp \left(i\left({\frac {\theta +2k\pi }{n}}\right)\right),\quad k=0,1,\ldots ,n-1.$

One may observe that

$z_{k}=z_{k-1}e^{i\theta /n};$ or, equivalently, $z_{k}=z_{0}e^{ik\theta /n},\quad k=1,2,\ldots ,n-1.$

Geometrically it means that the roots form a regular n-sided polygon centred at the origin; the vertices of the polygon belong to the circle of radius ${\sqrt[{n}]{r}}.$

Particularly important are the roots of unity, i.e. solutions of $z^{n}=1$. The cubic roots of 1 (with n=3) are

$1,\,-{\frac {1}{2}}+i{\frac {\sqrt {3}}{2}},\,-{\frac {1}{2}}-i{\frac {\sqrt {3}}{2}}$

and for n=4 we have

${\frac {1}{2}}+{\frac {\sqrt {2}}{2}},\,{\frac {1}{2}}-{\frac {\sqrt {2}}{2}},\,{\frac {1}{2}}+{\frac {\sqrt {2}}{2}},\,-{\frac {1}{2}}-{\frac {\sqrt {2}}{2}}.$