ArcSin

complex map of $u\!+\!\mathrm {i} v\!=\!\arcsin(x\!+\!\mathrm {i} y)$

ArcSin, or asign, or arcsin is holomorphic function, inverse of sin.

ArcSin is considered as elementary function

$f=\arcsin(z)$ is holomorphic solution $f$ of equation

$\sin(f)=z$

such that $\arcsin(0)\!=\!0$

Range of holomorphism

$\arcsin(z)$ is holomorphic in the whole complex plane except the halflines $z\!\leq \!-1$ and $z\!\geq \!1$.

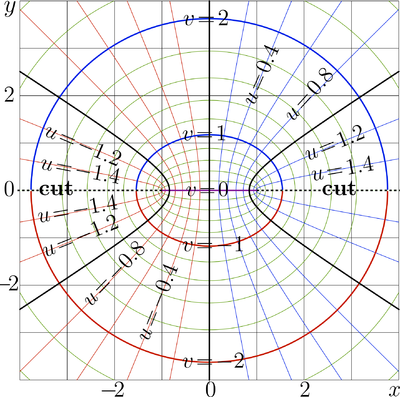
Complex map or </math>f=\arcsin(x+\mathrm i y)</math> is shown in figure at right in the $x$, $y$ plane with levels $u=\Re (f)=\mathrm {const}$ and levels $v=\Im (f)=\mathrm {const}$. Thick lines correspond to the Integer values. The cut lines are shown with dashed lines. In vicinity of the cut lines, the real part of ArcSin approach values $\pm \pi /2$.

Real values

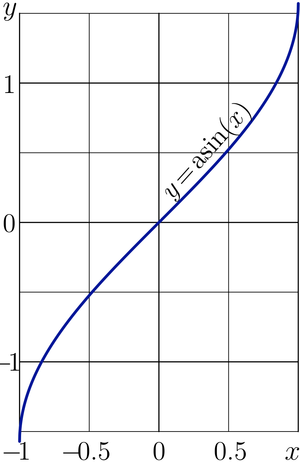
While $-1\leq x\leq 1$, id est, along the real axis, $\arcsin(x)$ has real values. The graphic is plotted at figure at right.

Numerical Implementation of ArcSin

In some programing languages, acos is implemented only for real argument. However, it can be expressed through the log function as follows:

complex double asin(complex double z){
if(Im(z)<0){if(Re(z)>=0){return M_PI/2.-I*log( z + sqrt(z*z-1.) );} 
                    else{return M_PI/2.-I*log( z - sqrt(z*z-1.) );}}
            if(Re(z)>=0){return M_PI/2.+I*log( z + sqrt(z*z-1.) );} 
                   else {return M_PI/2.+I*log( z - sqrt(z*z-1.) );} }

where I denotes the imaginary unity; Re and Im denote the real and imaginary parts; M_PI denotes $\pi$.

Fortunately, in the C++ compilers, function log is already implemented for complex double argument.

This implementation above used to plot the complex map of ArcSin at the top figure. In particular, the same representation can be used for real values of the argument; the explicit plot of ArcSin is generated with the same representation. (Click the figure to see the code used for its generation.) However, the last graphic could be generated also with the internal C++ function asin of real argument, as well as with flipping of plot of function sin.

Expansions

Expansion at zero

Often, the expansions of Sin and ArcSin at small values of argument are used;

$\displaystyle \!\!\!\!\!\!\!\!\!\sin(z)=z-{\frac {z^{3}}{3!}}+{\frac {z^{5}}{5!}}-{\frac {z^{7}}{7!}}+...$

$\displaystyle \!\!\!\!\!\!\!\!\!\arcsin(z)=z+{\frac {z^{3}}{3!}}+{\frac {3z^{5}}{40}}+{\frac {5z^{7}}{112}}+...$

Mathematica allows to evaluate many terms of this expantion:
arcsin(z) = z + 0.166666666666667 z³ + 0.0750000000000000 z⁵ + 0.0446428571428571 z⁷ + 0.0303819444444444 z⁹ + 0.0223721590909091 z¹¹ + 0.0173527644230769 z¹³ + 0.0139648437500000 z¹⁵ + 0.0115518008961397 z¹⁷ + 0.00976160952919408 z¹⁹ + 0.00839033580961682 z²¹ + 0.00731252587359885 z²³ + 0.00644721031188965 z²⁵ + ..

Expansion in vicinity of the branchpoints

Extremums of function Sin correspond to branch points of ArcSin. The expansions can be written as follows: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \!\!\!\!\!\!\!\!\! \sin\left( - \frac{\pi}{2}+t\right) = -1+ \frac{t^2}{2}-\frac{t^4}{24}+\frac{t^6}{720}-\frac{t^8}{40320}+..}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \!\!\!\!\!\!\!\!\! \arcsin(-1+t) = -\frac{\pi}{2}+\sqrt{2\,t} +\frac{t^{3/2}}{6\sqrt{2}}+\frac{ 5~ t^{5/2}}{80 \sqrt{2}}+ .. }

Mathematica allows to evaluate many of terms of this expansion;

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle \!\!\!\!\!\!\!\!\! \arcsin(-1+t) =- 1.5707963267948966 $ $+ \sqrt{t} ~ \Big($ $ 1.4142135623730950 $ $ +0.117851130 19775792 t$ $ +0.026516504294495532 t^2$ $+0.0078918167543141465 t^3$ $+0.0026854098677874526 t^4$ $+0.00098871908768538028 t^5$ $+0.00038344554362157376 t^6$ $+0.00015429118302868087 t^7$ $+0.000063815287098259552 t^8$ $+0.000026962891771048261 t^9$ $+0.000011587623725414788 t^{10}$ $ +0.0000050495474929920175 t^{11} $ $ +0.0000022260088531606476 t^{12} +... \Big)}

Similar expansion of ArcSin can be written at another branch point:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \arcsin(1-t) =-\arcsin(-1+t) }

The expansions above allow to evaluate ArcSin at least in vicinity of the segment Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [-1,1]} ; the precision of evaluation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s_0\approx \arcsin(z)} can be improved with the iteration

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle s_{n+1}=s_n+\frac{z-\sin(s_n)}{\sin'(s_n)}=s_n+\frac{z-\sin(s_n)}{\cos(s_n)} }

Keywords

sin, cos, elementary function, inverse function, complex map, C++

References

Some part of the content above is copypasted from TORI, http://tori.ils.uec.ac.jp/TORI/index.php/ArcSin