User:John R. Brews/Sandbox
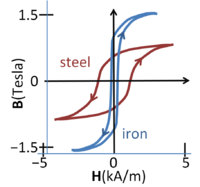
Add image caption here.Magnetic flux density vs. magnetic field in steel and iron; the curve depends upon the direction of traversal, the phenomenon of hysteresis
In the above argument the influence of atoms upon each other was neglected. For ferromagnetic materials that approximation is invalid. The self-interaction of the atoms tends to align them even when no external magnetic field is present. As a result, ferromagnetic materials create a net magnetic field (and magnetic flux density) in the space surrounding the material, and can form permanent magnets at temperatures below the Curie temperature of the material. At higher temperatures, the aligning interaction is inadequate to overcome the randomness introduced by thermal motions.
The figure shows magnetization curves for two different ferromagnetic materials. The curves exhibit hysteresis, that is, the curve is history dependent and, in particular, depends upon the direction in which the magnetic field increases. This complex behavior indicates that magnetization in such materials is not an equilibrium process, and larger samples break up into magnetic domains or sub-regions of different magnetization directions separated by domain walls.[1] The magnetization curve is affected (in part) by the change in size of the various domains as they adapt to changes in the external field.
A simplified "toy" example of ferromagnetism helps to understand the approach. The example follows Kittel.[2] We suppose that each atom is subject to a magnetic field due to the other atoms that is proportional to their magnetization:
where λ is a dimensionless proportionality factor, and the subscript E stands for exchange field, a technical term referring to the mechanism causing cooperation between the atoms.[3] We now bootstrap the calculation of the magnetization by assuming the total magnetic field is the applied field Ha plus the exchange field, and their sum induces the magnetization. Thus,
where the approximation is made that the magnetization is simply a linear response to the magnetic field, according to the simple scalar susceptibility χ. Then with the previous expression for HE,
or:
Because the denominator can become small, the coefficient of H can become large, and is called the "enhanced susceptibility".[4] A point of interest is that the denominator can be zero if χλ can be as large as one, which means we have an infinite magnetization with even a very small applied magnetic field. The implication is that the self-generated field can result in a magnetization with zero applied magnetic field. That is the phenomenon of ferromagnetism.
Today it is still impossible to predict from first principles that iron is ferromagnetic.[5] However, some guidance can be obtained as to which metals are candidates, and which are not, based upon estimates of how exchange energy varies with atomic radii and spacing.
- ↑ F Fiorillo, C Appino and M Pasquale (2005). “§1.3 Energy in a magnetic system. Domain walls and domain structures”, Isaak D. Mayergoyz, Giorgio Bertotti, editors: The Science of Hysteresis, volume III. Elsevier Academic Press, pp. 29 ff. ISBN 0123694337.
- ↑ This is the same reference cited above, but a different chapter: Kittel. “Chapter 12: Ferromagnetism and antiferromagnetism”, Introduction to solid state physics, pp. 321 ff. ISBN 978-0-471-41526-8.
- ↑ The idea is that electrons obey the Pauli exclusion principle that no two can occupy the same quantum state. That means configurations with aligned spins are energetically favored over misaligned spins by an exchange interaction, favoring magnetization. The same idea underlies Hund's rules for atoms, namely, other things equal, electrons in atoms populate states to maximize their total spin. Of course, an unanswered question is why ferromagnetic materials profit from this effect more than other materials. See LD Landau and EM Lifshitz (1960). “Chapter V: Ferromagnetism”, Electrodynamics of continuous media. Pergamon Press, pp. 146 ff. , and for some simple examples Assa Auerbach (1999). “Chapter 2: Spin exchange”, Interacting electrons and quantum magnetism. Springer, pp. 11 ff. ISBN 0387942866. .
- ↑ Same reference as previously, but p. 169:J Kübler (2009). “§4.1.1 Stoner theory”, Theory of itinerant electron magnetism, Revised ed. Oxford, pp. 169 ff. ISBN 0199559023.
- ↑ Bernard Dennis Cullity, Chad D. Graham (2009). “Chapter 4: Ferromagnetism”, Introduction to magnetic materials, 2nd ed. Wiley-IEEE, p. 131. ISBN 0471477419.



