User:Paul Schächterle/Notebook/LDR

Law of diminishing returns (Raw draft)

The law of diminishing returns (in this article referred to as LDR) is a concept in economic theory. It states that the output per input (productivity) declines if the input of a production factor is increased over a certain limit. Under the name law of diminishing returns actually exist two different concepts: one classical and one neoclassical. These concepts bear similarities but are based on different reasons.

The classical concept

Production function (blue) with first rising and then diminishing marginal (green) and average (magenta) returns.

In classical economics the LDR states the following: If you have at least two different production factors, the highest productivity is gained if an optimal proportion between these factors is kept. Any divergence from that proportion will result in lower productivity.

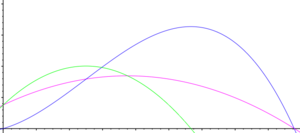
If one production factor is fixed, the proportion between the production factors will change with rising production i.e. rising input of the variable factor. According to the classical LDR this leads to a production function that has four phases with the following characteristics:

1. Rising marginal productivity, rising average productivity.
2. Diminishing marginal productivity, rising average productivity.
3. Diminishing average productivity.
4. Negative marginal productivity, i.e. an increase of the variable factor will result in a decrease of the overall product.

History

Historically the concept was first developed by Anne Robert Jacques Turgot. It was mainly related to agricultural production and the use of labour and later fertilizer in relation to a fixed amount of soil.

(more Material)

Critique

A production factor is only fixed if it is indivisible or if it is limited. Therefore it is generally possible to produce with an optimal proportion of factors and to use any available excess portion of one factor in a different area. Thus the classical LDR is closer related to business studies than to economics or political economy.

(Ref.)

The neoclassical concept

Production function (blue) with decreasing returns to scale (green) and therefore decreasing average returns (magenta).

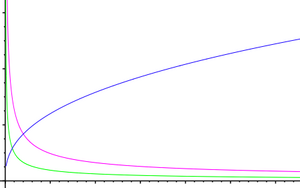
In neoclassical economics the LDR signifies that an increasing input of any production factor will result in diminishing marginal productivity. This leads to a production function with the following characteristics:

• Zero input of a production factor results in zero output i.e. the graph starts at the origin.
• Marginal productivity is highest with the lowest possible input, i.e. the point closest to an input of zero.
• Marginal productivity decreases continuously.

History

The origins of the neoclassical production function i.e. the neoclassical LDR date back to the time of classical economics. Then the concept was used to describe the effect of an increase in wheat production where good soils were limited. To increase the production of wheat inferior soils would have to be used, which would deliver less wheat for the same amount of labour.

(Ref. David Ricardo, 1772—1823, An Essay on Profits, 1815)

(Ref. to Malthus?)

Neoclassical economists extended the idea to the claim that any economically rational producer would use any production factor first for the most productive task, then for the next productive task, etc., and/or would use the best unit first, then the second best, etc. (Ref. to whom?) Thus the idea got applied to all production factors. This implies of course that there are different tasks with different productivities and/or units of different quality.

(Ref. <F/H, S. 55, Fn. 4> --> english equivalent?)

Implications

The general validity of the neoclassical LDR is a necessary assumption in the General Equilibrium Theory.

Critique

The LDR is based on at least one of the following necessary assumptions:

• The quality of the units of a factor differs and this is known to and controllable by the producer, so that she/he can chose the better units over inferior ones (classical argument/wheat production).
• There are different fields of application for the units of a factor, that have different productivity, so that the producer can chose productive uses over less productives.

(Ref ?)

Possibly: Aggregation problems, compare [1]

The general application of the neoclassical LDR rules out rising marginal productivity and is therefore contrary to the economies of scale. (Ref ?) Business studies do not rule out rising marginal productivity and therefore do not accept the general validity of the neoclassical LDR. (Ref.) According to a survey among business leaders, businesses do not calculate with falling marginal productivity. (Ref: Check: Eiteman/Guthrie 1952)

Combining both concepts

Cobb-Douglas production function with 2 factors and production elasticity complying to the neoclassical LDR, i.e. overall decreasing returns to scale.

Neoclassical theory usually distinguishes between only two factors of production: capital and labour. With just two factors of production the production function can be represented by a 3-dimensional graph.

Tho most prominent production function for creating such a graph is the Cobb-Douglas production function: Y = A × C^a × L^b, where Y stands for yield, C for capital, L for labour, and A, a and b are constants that can be interpreted as A for technology level and a and b for the production elasticities of the factors. This formula can contain elements of both concepts, the classical and the neoclassical LDR.

The classical concept is represented by the fact that a combination of both factors results in a square output so that an even proportion between the factors results in higher productivity.

The neoclassical concept is represented by the fact that each factor has diminishing returns to scale as long as (a < 1) and (b < 1). Note that the combined input of both factors only results in diminishing returns as long as (a + b < 1). If both factors independently have decreasing returns to scale (a < 1, b < 1), their combination might still lead to increasing returns to scale (a + b > 1).

For an interactive demonstration of the Cobb-Douglas production function see: [2]

Naming conventions

Viewing their attributed originators the names for both concepts may seem misleading. Turgot is considered physiocrat, not classical economist, and Ricardo is considered classical, not neoclassical economist. Yet the names of both concepts reflect the eras of their further development and refinement.