File:LambertWmapT.png
Original file (1,773 × 1,752 pixels, file size: 616 KB, MIME type: image/png)
Summary
| Title / Description
|
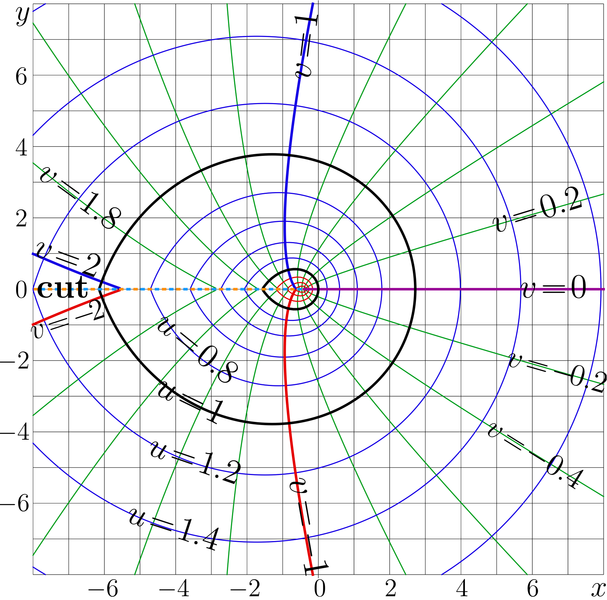
Complex map of the Principal branch of the Lambert W function |
|---|---|
| Citizendium author & Copyright holder
|
Copyright © Dmitrii Kouznetsov. See below for licence/re-use information. |
| Date created
|
2011 September 25 |
| Country of first publication
|
Japan |
| Notes
|
The Tania function is used for the evaluation; files conto.cin and ado.cin are used for the plotting. |
| Other versions
|
http://tori.ils.uec.ac.jp/TORI/index.php/File:LambertWmap150.png |
| Using this image on CZ
|
, then copy the code below to add this image to a Citizendium article, changing the size, alignment, and caption as necessary.
|
Please send email to manager A T citizendium.org .
Licensing
This media, LambertWmapT.png, is licenced under the Creative Commons Attribution 3.0 Unported License
You are free:
To Share — To copy, distribute and transmit the work; To Remix — To adapt the work.
Under the following conditions:
Attribution — You must attribute the work in the manner specified by the author or licensor (but not in any way that suggests that they endorse you or your use of the work).
For any reuse or distribution, you must make clear to others the licence terms of this work (the best way to do this is with a link to this licence's web page). Any of the above conditions can be waived if you get permission from the copyright holder. Nothing in this licence impairs or restricts the author's moral rights.
Read the full licence.
Generators
First, the curves are generated with the C++ program. The principal branch of the Lambert W function is easy to evaluate through the Tania function, the code is supplied below. Then, the labels are added in the Latex document. The result is converted to PNG or any other appropriate format.
C++ generator of the curves
Files conto.cin and ado.cin should be in the working directory for the compilation of the code below:
#include <math.h> #include <stdio.h> #include <stdlib.h> #define DB double #define DO(x,y) for(x=0;x<y;x++) using namespace std; #include <complex> typedef complex<double> z_type; #define Re(x) x.real() #define Im(x) x.imag() #define I z_type(0.,1.) #include "conto.cin"
z_type ArcTania(z_type z) {return z + log(z) - 1. ;}
z_type ArcTaniap(z_type z) {return 1. + 1./z ;}
z_type TaniaTay(z_type z) { int n; z_type s;
s=1.+z*(.5+z*(1./16.+z*(-1./192.+z*(-1./3072.+z*(1.3/6144.+z*(-4.7/147456.
//+z*(7.3/4128768.) //some reserve term
)))))); DO(n,3) s+=(z-ArcTania(s))/ArcTaniap(s); return s ; }
z_type TaniaNega(z_type z){int n;z_type s=exp(z-exp(z)+1.);
DO(n,4) s+=(z-ArcTania(s))/ArcTaniap(s); return s ; }
z_type TaniaBig(z_type z){int n;z_type s=z; s=z-log(s)+1.;
DO(n,3) s+=(z-ArcTania(s))/ArcTaniap(s); return s ; }
z_type TaniaS(z_type z){int n; z_type s,t=z+z_type(2.,-M_PI);t*=2./9.; t=I*sqrt(t);
s=-1.+t*(3.+t*(-3.+t*(.75+t*(.3+t*(.9/16.+t*(-.3/7.+t*(-12.51/224. //+t*(-.9/28.)
)))))));
DO(n,3) s+=(z-ArcTania(s))/ArcTaniap(s); return s ; }
z_type Tania(z_type z){ z_type t;
if( fabs(Im(z))< M_PI && Re(z)<-2.51) return TaniaNega(z);
if( abs(z)>7. || Re(z)>3.8 ) return TaniaBig(z);
if( Im(z) > .7 ) return TaniaS(z);
if( Im(z) < -.7) return conj(TaniaS(conj(z)));
return TaniaTay(z);
}
main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d;
int M=160,M1=M+1;
int N=161,N1=N+1;
DB X[M1],Y[N1], g[M1*N1],f[M1*N1], w[M1*N1]; // w is working array.
char v[M1*N1]; // v is working array
//FILE *o;o=fopen("productlogmap.eps","w");ado(o,162,162);
FILE *o;o=fopen("lambertwmap.eps","w");ado(o,162,162);
fprintf(o,"81 81 translate\n 10 10 scale\n");
DO(m,M1) X[m]=-8.+.1*(m);
DO(n,80)Y[n]=-8.+.1*n;
Y[80]=-.03;
Y[81]= .03;
for(n=82;n<N1;n++) Y[n]=-8.+.1*(n-1.);
for(m=-8;m<9;m++){if(m==0){M(m,-8.5)L(m,8.5)} else{M(m,-8)L(m,8)}}
for(n=-8;n<9;n++){ M( -8,n)L(8,n)}
fprintf(o,".008 W 0 0 0 RGB S\n");
DO(m,M1)DO(n,N1){g[m*N1+n]=9999; f[m*N1+n]=9999;}
DO(m,M1){x=X[m]; //printf("%5.2f\n",x);
DO(n,N1){y=Y[n]; z=z_type(x,y);
c=Tania(log(z)-1.); p=Re(c);q=Im(c);
if(p>-99. && p<99. && q>-99. && q<99. ){ g[m*N1+n]=p;f[m*N1+n]=q;}
}}
fprintf(o,"1 setlinejoin 2 setlinecap\n"); p=.6;q=.5;
for(m=-10;m<10;m++)for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N,(m+.1*n),-q, q); fprintf(o,".03 W 0 .6 0 RGB S\n");
for(m=0;m<10;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N,-(m+.1*n),-q, q); fprintf(o,".03 W .9 0 0 RGB S\n");
for(m=0;m<10;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, (m+.1*n),-q, q); fprintf(o,".03 W 0 0 .9 RGB S\n");
for(m=1;m<10;m++) conto(o,f,w,v,X,Y,M,N, (0.-m),-p,p); fprintf(o,".07 W .9 0 0 RGB S\n");
for(m=1;m<10;m++) conto(o,f,w,v,X,Y,M,N, (0.+m),-p,p); fprintf(o,".07 W 0 0 .9 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (0. ),-p,p); fprintf(o,".07 W .6 0 .6 RGB S\n");
for(m=-9;m<10;m++) conto(o,g,w,v,X,Y,M,N, (0.+m),-p,p); fprintf(o,".07 W 0 0 0 RGB S\n");
y=0.; for(m=0;m<75;m+=4) {x=-7.95+.1*m; M(x,y) L(x+.05,y)}
fprintf(o,".07 W 1 .6 0 RGB S\n");
y=0.; for(m=2;m<75;m+=4) {x=-7.95+.1*m; M(x,y) L(x+.05,y)}
fprintf(o,".07 W 0 .6 1 RGB S\n");
fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
system("epstopdf lambertwmap.eps");
system( "open lambertwmap.pdf");
getchar(); system("killall Preview");
}
Latex document generating the labels
\documentclass[12pt]{article} %
\usepackage{geometry} %
\usepackage{graphicx} %
\usepackage{rotating} %
\paperwidth 854pt %
\paperheight 844pt %
\topmargin -96pt %
\oddsidemargin -98pt %
\textwidth 1100pt %
\textheight 1100pt %
\pagestyle {empty} %
\newcommand \sx {\scalebox} %
\newcommand \rot {\begin{rotate}} %
\newcommand \ero {\end{rotate}} %
\newcommand \ing {\includegraphics} %
\begin{document} %
\sx{5}{ \begin{picture}(164,165) %
%\put(6,5){\ing{taniacontour}} %
%\put(6,5){\ing{productlogmap}} %
\put(6,5){\ing{lambertwmap}} %
\put(2,162){\sx{.7}{$y$}} %
\put(2,144){\sx{.6}{$6$}} %
\put(2,124){\sx{.6}{$4$}} %
\put(2,104){\sx{.6}{$2$}} %
\put(4,118){ \sx{.8}{\rot{-36}$v\!=\!1.8$\ero}} %
\put(3,96){ \sx{.8}{\rot{-20}$v\!=\!2$\ero}} %
\put(2, 84){\sx{.6}{$0$}} %
\put(8, 84){\sx{.8}{\bf cut}} %
\put(7,72){\sx{.7}{\rot{18}$v\!=\!-\!2$\ero}} %
\put(-3,64){\sx{.6}{$-2$}} %
\put(-3,44){\sx{.6}{$-4$}} %
\put(-3,24){\sx{.6}{$-6$}} %
\put( 22,0){\sx{.6}{$-6$}} %
\put( 42,0){\sx{.6}{$-4$}} %
\put( 62,0){\sx{.6}{$-2$}} %
\put( 86,0){\sx{.6}{$0$}} %
\put(106,0){\sx{.6}{$2$}} %
\put(126,0){\sx{.6}{$4$}} %
\put(146,0){\sx{.6}{$6$}} %
\put(164,0){\sx{.7}{$x$}} %
\put( 41, 76){\rot{-39}\sx{.8}{$u\!=\!0.8$}\ero}%
\put( 41, 57){\rot{-26}\sx{.84}{$u\!=\!1$}\ero}%
\put( 39, 40){\rot{-19}\sx{.8}{$u\!=\!1.2$}\ero}%
\put( 33, 21){\rot{-18}\sx{.8}{$u\!=\!1.4$}\ero}%
\put( 85, 145){\rot{83}\sx{.82}{$v\!=\!1$}\ero}%
\put(137, 102){\rot{17}\sx{.8}{$v\!=\!0.2$}\ero}%
\put(144, 84){\rot{0}\sx{.8}{$v\!=\!0$}\ero}%
\put(140, 65){\rot{-16}\sx{.72}{$v\!=\!-\!0.2$}\ero}%
\put(134, 46){\rot{-32}\sx{.72}{$v\!=\!-0.4$}\ero}%
\put( 79, 33){\rot{-80}\sx{.86}{$v\!=\!-1$}\ero}%
\end{picture} %
} %
\end{document}
% Copyleft 2011 by Dmitrii Kouznetsov. The free use is allowed, but, please, attribute the source. It is not for any "priority", but to trace errors if any. Dmitrii Kouznetsov 02:08, 26 September 2011 (UTC)
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 18:51, 11 March 2022 |  | 1,773 × 1,752 (616 KB) | Maintenance script (talk | contribs) | == Summary == Importing file |
You cannot overwrite this file.
File usage
The following page uses this file: