Work (physics)
Definition of mechanical work
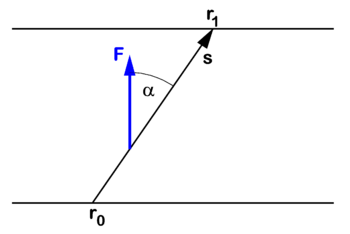
As stated, mechanical work W is force times path length: When a constant force F acts on a body along a straight path and the body is moved over a length |s| along this path, then
Here s is vector of magnitude |s| along the path. The inner product between the two vectors F and s is the product of their magnitudes |F| and |s| times the cosine of the angle, α, between the vectors.
When the force is directed along the path (F and s parallel), α = 0, cosα = 1, and we have simply W = |F| |s|.
When a force is perpendicular to the path, α = 90°, cosα = 0, the force performs no work. Examples of such a situation are the centrifugal force on a mass in uniform circular motion and the gravitational force acting on a satellite in a circular orbit. If a body is in uniform (i.e., has constant speed) straight motion and the only force acting on it is perpendicular to its path, then the body will persist in its uniform straight motion (Newton's first law).
When a force F is anti-parallel to the path (α = 180°), it performs negative work W < 0, since cosα = −1, and |F| and |s| are both greater than zero. Work being a form of energy, it is conserved; the negative work done by the force is converted into a decrease of the kinetic energy T:
- W = ΔT ≡ T1 − T0
(both sides of the equation are negative, W because path and force are anti-parallel, ΔT because T decreases, i.e., T1 < T0 ).
For example, think of an old-fashioned type of cannon that shoots a cannon ball of mass m straight up. The gun powder explosion gives the ball initial kinetic energy T0 = ½ m v02. The gravitational attraction of the earth performs negative work (force downward, motion of the cannon ball upward), until at the highest point the speed and the kinetic energy of the ball are zero. The amount of work performed is ΔT ≡ 0−T0 = −T0. At the highest point the motion of the cannon ball reverts direction, it starts falling to earth, and from there on the gravitational attraction performs positive work (direction of motion and force are parallel). The kinetic energy increases again until it achieves its original value T0 = ½ m v02 at the point where the cannon ball arrives again at the cannon. The total work done by the gravitation is zero, the work done on the cannon ball going up cancels the work done on the ball going down. (In this example we ignore friction by the air).
When the the force is conservative (non-dissipative), the work is independent of path, and when furthermore the path is a closed curve, the total work is zero (one way the work is positive and the other way the work is equally large in absolute value, but negative).
As the gravitational field is conservative, we just saw an example of a mass (a cannon ball) making a closed path in a conservative force field. The potential energy U of a mass m close to the surface of the earth is equal to U = mgh, where g is the gravitational acceleration and h is the height. Assuming that the cannon is positioned on height h = 0, the cannon ball starts with potential energy zero, U0 = 0. The work W done by the gravitational field on the cannon ball going upward has two effects: it decreases its kinetic energy—as just discussed—and it increases its potential energy, U1 > U0, so that
- W = −ΔU ≡ −(U1 − U0) = U0 − U1 < 0.
At the highest point, hmax, the potential energy is maximum U1 = mghmax (equal to minus the work performed) and the kinetic energy is zero (this is the point where the motion of the cannon ball changes direction, for a small amount of time its speed is zero). The work done by a conservative force converts a decrease in kinetic energy into an increase of potential energy and conversely:
- W = ΔT = −ΔU, so that ΔT + ΔU = 0.
When the cannon ball dropping down is at height h = 0 again, its kinetic energy is maximum (equal to the energy imparted to it by the gun powder) and its potential energy is zero again.