Fluid flow past a cylinder

"The flow of an incompressible fluid past a cylinder is one of the first mathematical models that a student of fluid dynamics encounters. This flow is an excellent vehicle for the study of concepts that will be encountered numerous times in mathematical physics, such as vector fields, coordinate transformations, and most important, the physical interpretation of mathematical results."

Mathematical Solution

PD Image
Colors: pressure field. Red is high and blue is low. Velocity vectors.

PD Image
Close-up view of one quadrant of the flow. Colors: pressure field. Red is high and blue is low. Velocity vectors.

Pressure field (colors), streamfunction (black), velocity potential (white).

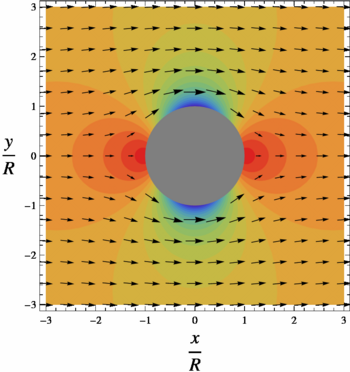
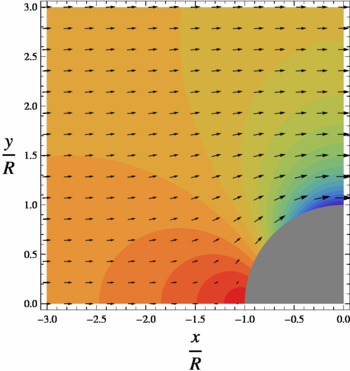
A cylinder (or disk) of radius $R$ is placed in two-dimensional, incompressible, inviscid flow. The goal is to find the steady velocity vector ${\vec {V}}$ and pressure $p$ in a plane, subject to the condition that far from the cylinder the velocity vector is

${\vec {V}}=U{\widehat {i}}+0{\widehat {j}}$

and at the boundary of the cylinder

${\vec {V}}\cdot {\widehat {n}}=0$

where ${\widehat {n}}$ is vector normal to the cylinder surface. The upstream flow is uniform and has no vorticity. The flow is inviscid, incompressible and has constant mass density $\rho$. The flow therefore remains without vorticity, or is said to be irrotational, with $\nabla \times {\vec {V}}=0$ everywhere. Being irrotational, there must exist a velocity potential $\phi$:

${\vec {V}}=\nabla \phi$

Being incompressible, $\nabla \cdot {\vec {V}}=0$, so $\phi$ must satisify Laplace's equation:

$\nabla ^{2}\phi =0$

The solution for $\phi$ is obtained most easily in polar coordinates <matth>r</math> and $\theta$, related to conventional Cartesian coordinates by $x=r\cos \theta$ and $y=r\sin \theta$. In polar coordinates, Laplace's equation is:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial^2\phi}{\partial r^2} + \frac{1}{r}\frac{\partial \phi}{\partial r} + \frac{1}{r^2} \frac{\partial^2\phi}{\partial \theta^2}=0}

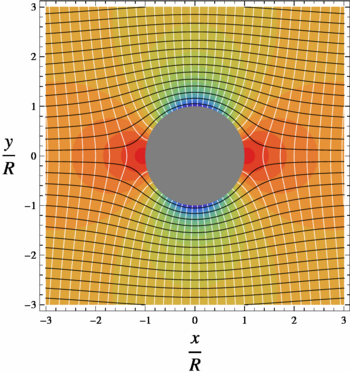
The solution that satisfies the boundary conditions is

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi(r,\theta)=U\left(r+\frac{R^2}{r}\right)\cos\theta}

The velocity components in polar coordinates are obtained from the components of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla\phi} in polar coordinates:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_r=\frac{\partial \phi}{\partial r} = U\left(1-\frac{R^2}{r^2}\right)\cos\theta}

and

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_\theta=\frac{1}{r}\frac{\partial \phi}{\partial \theta} = - U\left(1+\frac{R^2}{r^2}\right)\sin\theta}

Being invisicid and irrotational, Bernoulli's equation allows the solution for pressure field to be obtained directly form the velocity field:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p=\frac{1}{2}\rho\left(U^2-V^2\right) + p_\infty}

where the constants Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p_\infty} appear to that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p\rightarrow p_\infty } far from the cylinder, where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V=U} . Using Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V^2=V_r^2+V_\theta^2} ,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p=\frac{1}{2}\rho U^2\left(2\frac{R^2}{r^2}\cos(2\theta)-\frac{R^4}{r^4}\right) + p_\infty }