User:Louis F. Sander/Sandbox
The account of this former contributor was not re-activated after the server upgrade of March 2022.
| ARTICLE | LINK FOR PASTING INTO A BROWSER WINDOW |
| AHP article in Citizendium | http://en.citizendium.org/wiki/Analytic_Hierarchy_Process |
| AHP Development Page in Citizendium | http://en.citizendium.org/wiki/User:Louis_F._Sander/Analytic_Hierarchy_Process |
| AHP Sandbox in Citizendium | http://en.citizendium.org/wiki/User:Louis_F._Sander/Sandbox |
| AHP article in Wikipedia | http://en.wikipedia.org/wiki/Analytic_Hierarchy_Process |
| Thomas L. Saaty article in Citizendium | http://en.citizendium.org/wiki/Thomas_L._Saaty |
| Thomas L. Saaty article in Wikipedia | http://en.wikipedia.org/wiki/Thomas_L._Saaty |
| ANP article in Citizendium | http://en.citizendium.org/wiki/Analytic_Network_Process |
| ANP article in Wikipedia | http://en.wikipedia.org/wiki/Analytic_Network_Process |
| MCDM article in Citizendium | http://en.citizendium.org/wiki/MCDM |
| MCDM article in Wikipedia | http://en.wikipedia.org/wiki/MCDM |
| Canadian demo site | http://www.cci-icc.gc.ca/tools/ahp/index_e.asp |
| New AHP Article | |
| Wikipedia Sandbox/2 | http://en.wikipedia.org/wiki/User:Lou_Sander/Sandbox2 |
Removed material that should go back in:
As the family makes the pairwise comparisons, they should focus exclusively on Purchase Price, not allowing other attributes of the alternatives to influence the weights they give each member of the pair.
When we compare them in pairs with regard to their purchase price, we will make a total of 15 comparisons.[1]
Questions to ask the reading group:
This is intended to be very easy to understand for intelligent general readers. Is it?
- If it stays about the same size, where can it be improved? (Phrasing, wording, illustrations, points missed, etc. Also should some of the parts be rearranged / in a different sequence.)
- If we needed to cut it down in size, how could that be done?
- If we could make it up to twice as long as it is, what should we add?
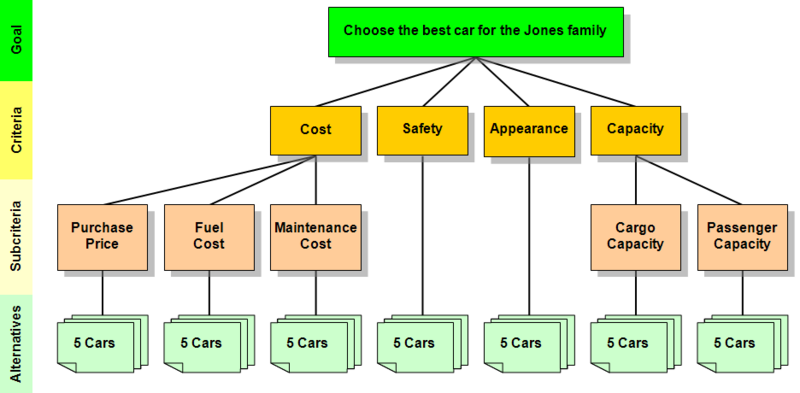
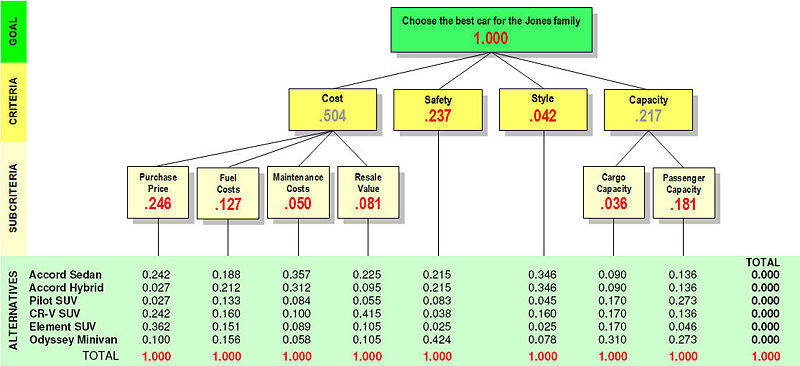
The Jones' hierarchy could be diagrammed like this:
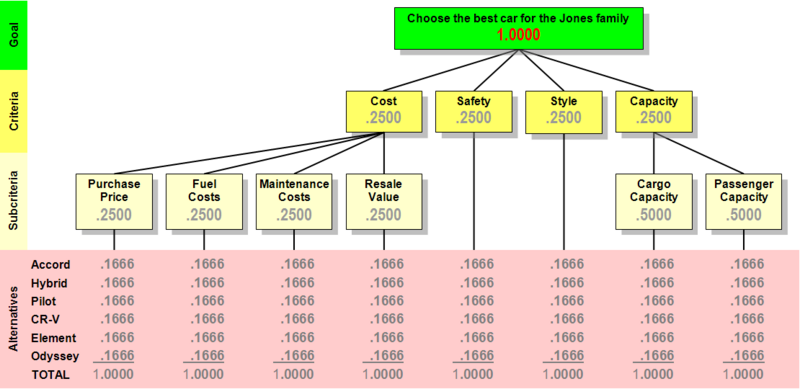
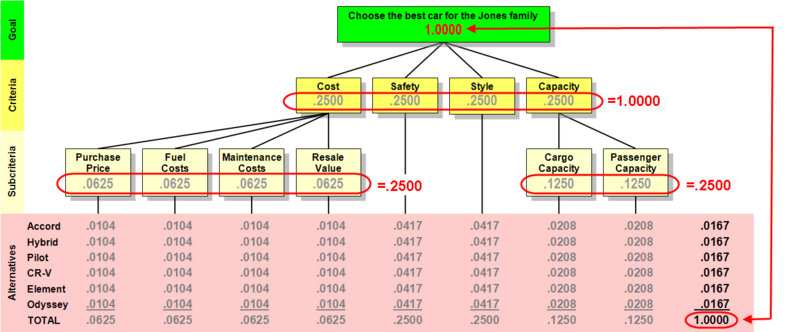
Fig. 1 - What Lou thinks are default LOCAL priorities. I have in mind using, throughout the article, gray for default priorities, black for local priorities, and red for global priorities. Maybe we need a better way to show totals for the Criteria and Subcriteria. Numbers are taken to four decimal places to reduce rounding errors; maybe that introduces too much visual confusion. Also the numbers in the pink need to be moved slightly to the left to line up better.

Fig. 1 - What Lou thinks are default LOCAL priorities. I have in mind using, throughout the article, gray for default priorities, black for local priorities, and red for global priorities. Maybe we need a better way to show totals for the Criteria and Subcriteria. Numbers are taken to four decimal places to reduce rounding errors; maybe that introduces too much visual confusion. Also the numbers in the pink need to be moved slightly to the left to line up better.
Nice Video
Nice Video, continued
Comments from Rozann on 2/11/08: These are absolute (counting) numbers, which are the best kind, per Rozann. Only useful when you have two things. (Except you can count people in a room.) Something that weighs twice as much as something else has a 2 associated with it, with respect to this weighting only. Paradigm shift: old was basing things on scales (such as foot, for the king's foot, which had an arbitrary origin). New is a relative view of the world. Not exactly how long was the king's foot, but how many times bigger is thing A than thing B. Relative scales have advantages and disadvantages. Find a better word, maybe, than "activities"
Notes
Aspects of AHP
- Computerized now, with gadgets
- Disciplined look at a decision (focus on objectives, alternatives, more than voting)
- Handles rational, intuitive, irrational, all at the same time (RS: maybe there is a better word than disciplined to capture this idea – though I can’t think what it might be right now. Somehow disciplined sounds too straightlaced, too mechanistic.)
- Permits explicit presentation of evaluation criteria (de Stiguer)
- Lets you compare the alternatives and fiddle with them, vs. just giving the best one
Miscellaneous
Selecting a spouse is important and has long-term consequences.
This is like logarithms, the LaPlace transform, etc., in that it replaces something hard to deal with with something much easier to deal with.
Get a bunch of unisex names to be used for alternatives in the spouse example. Search on unisex baby names, and you'll get more than you need. Chris, Pat, Morgan, Casey, Lee, Payton, Mackenzie, Sam. Short ones: Chris, Pat, Lee, Sam.
Good Stuff
Problems with high stakes, involving human perceptions and judgements, and whose resolutions have long-term repercussions, call for a rational approach to their solution. (Bhushan promo)
You might also want to read the paper "The Analytic Hierarchy Process - An Exposition," E.J. Forman and S. I. Gass, Operations Research, 49, 4, July-August, 2001, pp. 469-486. (Saul Gass, U of MD) (RS: Forman and Tom originally started the Expert Choice company in 1983 as partners, and Forman still runs Expert Choice. Would using this article be in conflict with the “no vested interest” Wikipedia requirement?)
Potential References
- Book: Natural Resource and Environmental Decision Making
- Chapter: Decision by Objectives (Forman & Selly)
Older and/or less useful
- Abstract: The Analytic Hierarchy Process and Participatory Decisionmaking (USDA Forest Service, 1995)
- Full text of the above
- Composite Indicators/Weighting (European Commission)
- Abstract: The Analytic Hierarchy Process in Medical Decisionmaking (1989)
- Paper: Some Comments on the Analytic Hierarchy Process (Criticism, 1990)
Rank reversal
(This was considered for an intro to the rank reversal phenomenon. It has possibilities.)
Many criticisms of AHP have involved a phenomenon called "rank reversal." We will discuss that phenomenon here.
In its simplest form, decision making involves ranking alternatives in terms of criteria or attributes of the alternatives. If we want to make a decision, for example, about the cost of several food items, it is easy to rank them based on price. We could show several alternatives in a list like this:
- Small hamburger $1.00
- Large hamburger $2.00
- Jumbo hamburger $3.00
Let's say that a new alternative comes onto the scene: a large extra juicy cheeseburger, featured today for only $1.75. it will fit nicely into the list, without affecting the ranking of the existing alternatives. Small is still ahead of large, and large is still ahead of jumbo. Our ranking now becomes:
- Small hamburger $1.00
- Large extra juicy cheeseburger $1.75
- Large hamburger $2.00
- Jumbo hamburger $3.00
If other alternatives are added to the list, they, too, can fit into their appropriate places, without disturbing the rank order of the previous ones. Importantly, everyone deciding which item to buy can agree exactly on the rank order of the list. If several other items were added at $1.75, we might not know how to rank all the $1.75 items among themselves, but the ranking of the original items would still be preserved.
Drafts of possible sections
Pairwise Comparisons
In AHP, we rank a group of items (RS: on some property they have -- the overall ranking is obtained after synthesizing the priority vector results for all the properties) by comparing them to each other in pairs. If the group has more than a very few items, this can be very much easier than trying to rank all the items at once.
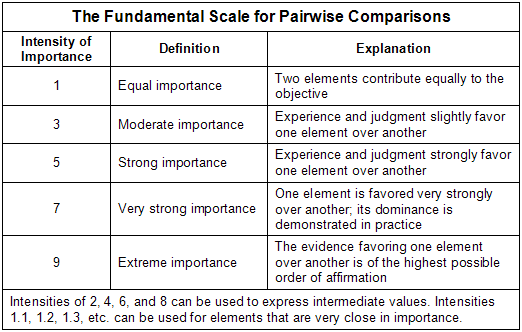
As we consider the pairs of items, we express the importance of one vs. the other by assigning it a weight from -9 to +9. (RS: no, an important distinction between AHP and other processes that directly assign numbers from 1 to 5 to items on some property is that the assigned number or judgment is always about the relation between a pair of items being compared and expresses how many times more the larger one is than the smaller one . We use numbers from 1 to 9. The negative numbers of the questionnaire are a convenience for soliciting judgments – they are actually inverses: 1/9, 1/8 and so on. It is easiest to see this if you form the matrix of judgments that results from the complete set of judgments of n items on a given property. Also RS: Lou – people use minus numbers instead of fractions because it is easier to present questionnaires that way and it is even easier to fill in matrices using a minus sign to indicate when the number is actually a reciprocal, instead of having to enter something like 1/3, but we really need to make it clear hat the actual math of the AHP does not use negative numbers.) To facilitate the assignment of weights, we can use a verbal scale ranging from "Much Less Important" to "Equally Important," to "Much More Important."
When we have finished all the comparisons in a group, AHP's mathematical algorithm evaluates our work and derives the appropriate overall weight for each of the items in the group. The greater the weight, the more important to us is the item to which it is assigned.
The algorithm also gives a numeric indicator of the consistency of our rankings. (If we greatly prefer apples to oranges, and greatly prefer oranges to turnips, it would be inconsistent to say that we also slightly prefer turnips to apples. When we say such a thing, AHP notices it and prompts us to reconsider. We may react to the prompting or not; after all we, not AHP, are making the judgments here.)
(RS: And though we can detect and note inconsistency, the AHP must allow inconsistencies because the real world is sometimes inconsistent, the Steelers beat the Giants, the Giants beat the Redskins and the Redskins beat the Steelers. Many decision theories prevent modeling such actual inconsistent events. In general it is better to be fairly consistent and that is why it is desirable to be able to point out to the judge where his inconsistency is – maybe he should at least think it over and see if he means that or not.)
Example
To illustrate the AHP technique of pairwise comparisons, let's use it on something that AHP is very well suited for: a problem with high stakes, involving human perceptions and judgments, whose resolution has long-term effects. To keep things simple, we'll choose a problem that is universally familiar, and we'll limit our comparisons to only three criteria.
Imagine that you want to evaluate, on a rational, disciplined basis, how important each of three criteria is to you in selecting a prospective spouse: Brains, Looks, and Personality. If we compare the criteria two by two, AHP can use our comparisons to assign a numerical weight to each of the three.
(LFS 3/30/08 - Maybe a good criterion would be something like "cost of maintenance." Think of the beautiful wife who spends all your money on clothes and makeup.)
You can make such an evaluation on THIS WEB SITE from the Canadian Conservation Institute. Here's what to do after opening the site:
- On the first screen, enter the number 3, to specify how many criteria you will be comparing.
- Click Continue, then enter the names of the criteria: Brains, Looks, and Personality. (To facilitate our discussion, please enter them in that order; normally, the order doesn't matter.)
- Scroll down and select the Line-by-Line method to facilitate entering the data.
- Click Continue and begin your pairwise comparisons. (Look at the bar chart and note that before you make any comparisons, all three criteria have equal importance.)
- For each of the three pairs of items, you will compare the first to the second by entering a number between -9 and 9. You can use the verbal scale to help you choose each number. (Example: If Brains were a little less important to you than Looks, you might enter -3 for this pair. If Brains were very much more important, you might enter a 9.) To facilitate our discussion, imagine that Brains are moderately more important to you than either Looks or Personality, and that you have no preference for Looks vs. Personality. Indicate these preferences by entering 5, 5, and 1 for the pairwise comparisons.
- Click Calculate to see the results of your work. The higher the number assigned to each criterion, the more important it is to you, based on your own pairwise comparisons. In our example, Brains accounts for 71.43% of your preference, and each of the others for 14.29%. (These numbers are a bit too precise to apply to the human situation involved, so we might just rely on the bar chart to compare them.)
- Look at the Consistency Ratio below the bar chart. If you've entered the numbers we asked you to, your consistency ratio will be zero, indicating that your comparisons were perfectly consistent. The Consistency Ratio is a measurement of the consistency of the data you entered (remember the apples, oranges, and turnips above). The higher the ratio, the less consistent were your entries. Whenever it is greater than 0.1 or so, you may want to review your entries to see if they really reflect your thinking.
The web site allows for easy modification of your judgments, and it can be instructive to change them and see how that affects the outcome. (The modification feature "times out" after a few minutes, after which you must start your evaluation from scratch.)
By experimenting with this small number of criteria, you can develop a feel for what AHP is doing. Keeping your first two comparisons the same, express a slight preference for Looks or Personality, and notice what happens to the results. Change your preferences in other ways, and see if you can follow the changes in results. (Don't worry too much about inconsistencies unless the ratio is larger than 0.1 or so -- inconsistency is a part of human nature, and we are dealing fairly closely with human nature here.)
To experiment at a more challenging level, enter a new problem with four criteria: Brains, Looks, Personality, and Wealth. With the larger number of criteria, it is harder to "see" how they interact, but the technique is every bit as valid. Imagine how difficult it would be for you, without the aid of AHP, to apply systematically-derived numerical weights to the six criteria of Brains, Looks, Personality, Wealth, Age, and Religion. Try it with AHP and see how simple such a thing can be. Once you've finished, see if you're pleased with the weights, and if you are comfortable about how they were derived.
Diverse perceptions and judgments
VERY ROUGH DRAFT OF THIS PART...
- AHP is a method of measuring perceptions and judgments in relative terms.
- Its inputs depend on the judgments of the participants/decision makers.
- It allows the consideration and combination of many kinds of judgments about the matter at hand, e.g., rational, intuitive, irrational, other(?).
- If the judgments are irrational, won't we likely get a clue to that from the Consistency Ratio?
Example (much smoother than the stuff above)
Most decisions require the decision maker(s) to consider price or cost. Compared to many other considerations in decision making, this one is simple, straightforward, and relatively free from emotional or subjective complexity.
When considering a pair of prices, it is obvious which is the higher and which is the lower; a calculator makes it easy to analyze the absolute and relative differences between the two. Given a longer list of prices, anyone can identify the lowest price and the highest one, and with the help of a spreadsheet program, can compute the exact numerical relationships between all the prices on the list.
But how can this information be applied to making a specific decision? Different decision makers can have very different ways of dealing with it; AHP can accommodate them all.
Take the familiar case of buying an automobile. The prices of the alternatives can be obtained from formal price quotations, and can be known exactly to the penny. After considering multiple bids on each of several autos, we might get a list like this:
- $18,285.00 - Chevrolet Cobalt
- $28,240.72 - Audi A4
- $34,885.50 - Chrysler 300
- $35,001.67 - Saab 9-5
- $43,548.31 - BMW 5 Series
As each decision maker makes pairwise comparisons of these numbers, he or she will apply their personal judgment to the task. Those judgments can be of various kinds, and whatever they are, AHP will capture them. Imagine different decision makers having these different thoughts as they consider various pairs of prices:
"We're comparing many other factors about these automobiles, but now that we're focusing on price,...
- ... prices are numbers, and numbers never lie. Two items should be preferred in exact proportion to their price, with the lower price being better. A $20,000 price is exactly twice as good as a $40,000 price, exactly 10% less good than a $22,000 price, and so forth. I will make my comparisons according to the irrefutable perfection of numbers."
- ... you should always go with the lowest responsible bidder. I'll always prefer the lower price as strongly as I can over the higher one."
- ... you get what you pay for. I'll always prefer the higher price as strongly as I can over the lower one."
- ... price is no object in this case. Since we have enough money to buy whatever car we want, it's the other considerations that should make the difference. I'll rank all prices as equally preferable."
- ... no automobile is worth $35,000. I'll do my best in comparing the less expensive ones, but I'll give anything over $35K as little weight as possible."
- ... I know that U.S. car companies are always flexible on price. They'll always come down when you press them, so I'll give extra preference to the Chevrolet and Chrysler whenever they're part of a comparison."
- ... I may not know cars, but I know my numerology. I'll add up the digits in each price, then keep adding the digits in the results until I'm down to a single digit. The closer it is to a seven, the more will I prefer it."
- ... I'll do the best I can at comparing the prices, but any car under $25K is a piece of junk, and I'll give it as little weight as possible."
- ... I've never been comfortable with numbers. I'll just guess."
- ... comparing these prices isn't as easy as it looks. But as an experienced purchasing manager who buys 500 autos a year, I'll apply my knowledge and judgment, and I'm sure it will work out well."
NOTE TO LOU: Do something like the above with the wealth aspect of choosing a spouse. Maybe consider current salary, personal net wealth, his/her (estimated?) share of family net wealth, etc.
NEW SUBJECT
EXERCISE FOR MBA CANDIDATES:
- Given the above list of prices, use Excel to calculate and display all the relationships between them.
- Now that you know all that stuff, how do you use it in deciding which car you want to buy?
References
- ↑ Yes, this is a lot of comparisons. And considering the other covering criteria we need to compare the alternatives to, we will have 15 x 8 = 120 comparisons in all.
Notes about this draft
Looking for the best format for this bibliography
Here we are trying to determine the best format for citing Saaty's books on this site.
The format for the books in the AHP series (above) seems to be a good one for our purpose, but it is different from the various "standard" formats that are commonly used for bibliographies.
Below are shown "started from scratch" citation examples for the same ISBN, cited in different formats using various tools. The tools aren't necessarily consistent. Authors vary. Titles vary, and might not include the longest version, which is probably what we want to show. Exact name of the publisher varies.
- Vargas, Luis G.; Saaty, Thomas L.; Kearns, Kevin Corrigan (1991). Analytical planning: the organization of systems. Pittsburgh, PA: RWS. ISBN 0-9620317-3-9. -- From Template Builder
- Saaty, Thomas (1991). Analytical Planning. Pittsburgh: RWS. ISBN 0962031739. -- From OttoBib in WP format
- (Complete WP format is HERE)
- Saaty, Thomas et.al. Analytical Planning. Pittsburgh: RWS, 1991. -- From OttoBib in MLA format
- Saaty, T., Kearns, K., & Vargas, L. (1991). Analytical Planning. Pittsburgh: RWS. -- From OttoBib in APA format
- Saaty, Thomas et.al. Analytical Planning. Pittsburgh: RWS, 1991. -- From OttoBib in Chicago/Turabian format
- This is what OttoBib gives for BibTeX format:
@Book{saaty1991,
author = 'Saaty, Thomas', title = 'Analytical Planning', publisher = 'RWS', year = '1991', address = 'Pittsburgh', isbn = '0962031739' }
"Cite Books" template
Wikipedia has a template called "Cite Books" that might be useful on Citizendium. See the details HERE. It looks pretty good, and seems to include most of the useful fields. It doesn't include the number of pages, though. Some of the items don't show up on Citizendium, but that's a minor problem that will probably disappear over time.
Here is a sample citation using the Wikipedia template. Edit this section to see the template and the entries that produced this listing:
- Author, Arthur; John Coauthor, Mary Coauthor [July 1989] (January 2007). Ed Itter: Lou Sander's Tips & Tricks for Commodore Computers, Gilt-edged edition. Pittsburgh, Pennsylvania: RWS Publications. ISBN 0-8306-3192-5. Retrieved on 2007-09-05. “This is a quotation from the book.”