Fuzzy subset

To be Completed !! Template:TOC-right

Introduction

The term fuzzy subset is a generalization of the subset concept from set theory. Observe that we can obtain a subset of a given set S by considering the extension of a well defined property P in S. Indeed, the axiom of comprehension reads that a subset B of S exists whose members are precisely those objects in S satisfying P. For example if S is the set of natural numbers and P is the property "to be prime", then the subset B of prime numbers is defined. Assume that P is a vague property as "to be big", "to be young": is there a way to define the extension of P ? For example:

is there a precise definition of the notion of set of big numbers ?

The notion of fuzzy subset

the fuzzy subset of small number and the fuzzy subset of numbers close to 6.

An attempt to give an answer to such a question was proposed in 1965 by Lotfi Zadeh and at the same time, by Dieter Klaua in the framework of multi-valued logic. Now recall that the characteristic function of a classical subset X of S is the map c_X : → {0,1} such that c_X(x) = 1 if x is an element in X and c_X(x) = 0 otherwise. Obviously, it is possible to identify every subset X with its characteristic function c_X and therefore the extension of a property with a suitable characteristic function. This suggests that we can define the subset of big elements by a generalized characteristic function in which instead of the Boolean algebra {0,1} we can consider, for example, the interval [0,1]. The following is a precise definition.

Definition. Let S be a nonempty set, then a fuzzy subset of S is a map s from S into [0,1]. We denote by [0,1]^S the class of all the fuzzy subsets of S. If S₁,...S_n are nonempty sets then a fuzzy subset of S₁×. . .×S_n is called an n-ary L-relation.

The elements in [0,1] are interpreted as truth values and, in accordance, for every x in S, the number s(x) is interpreted as the membership degree of x to s. We say that a fuzzy subset s is crisp if s(x) is in {0,1} for every x in S. By associating every classical subsets of S with its characteristic function, we can identify the subsets of S with the crisp fuzzy subsets. In particular we call "empty subset" of S the fuzzy subset of S constantly equal to 0. Notice that in such a way there is not a unique empty subsets.

Some set-theoretical notions for fuzzy subsets

the intersection of the fuzzy subset of small number with the fuzzy subset of numbers close to 6 (obtained by the minimum and the product).

In classical mathematics the definitions of union, intersection and complement are related with the interpretation of the basic logical connectives $\vee ,\wedge ,\neg$. In order to define the same operations for fuzzy subsets, we have to fix suitable operations $\oplus ,\otimes$ and ~ in [0,1] to interpret these connectives. Once this was done, we can set

$(s\cup t)(x)=s(x)\oplus t(x)$,

$(s\cap t)(x)=s(x)\otimes t(x)$,

$(-s)(x)=~s(x)$.

In such a way an algebraic structure $([0,1]^{S},\cup ,\cap ,-,\emptyset ,S)$ is defined and this structure is the direct power of the structure $([0,1],\oplus ,\otimes ,$ ~,0 ,1) with index set S. In Zadeh's original papers the operations $\oplus ,\otimes$, ~ are defined by setting for every x and y in [0,1]:

$x\otimes y$ = min(x, y) ; $x\oplus y$ = max(x,y) ; $~x$ = 1-x.

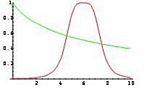
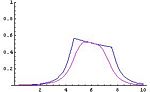
In such a case $([0,1]^{F},\cup ,\cap ,-,\emptyset ,S)$ is a complete, completely distributive lattice with an involution. Several authors prefer to consider different operations, as an example to assume that $\otimes$ is a triangular norm in [0,1] and that $\oplus$ is the corresponding triangular co-norm. For example, the picture represents the intersection of the fuzzy subset of small number with the fuzzy subset of numbers close to 6 obtained by the minimum and the product. In all the cases the interpretation of a logical connective is conservative in the sense that its restriction to {0,1} coincides with the classical one. This entails that the map associating any subset X of a set S with the related characteristic function is an embedding of the Boolean algebra $(\{0,1\}^{S},\cup ,\cap ,-,\emptyset ,S)$ into the algebra $(L^{S},\cup ,\cap ,-,\emptyset ,S)$.

L-subsets

The notion of fuzzy subset can be extended by substituting the interval [0,1] by any bounded lattice L. Again one assumes that in L suitable operations are defined to interpret the logical connectives. This extension was done mainly in the framework of fuzzy logic.

See also

• Fuzzy logic
• Fuzzy control system
• Neuro-fuzzy
• Fuzzy subalgebra
• Fuzzy associative matrix
• FuzzyCLIPS expert system
• Paradox of the heap
• Pattern recognition
• Rough set

Bibliography

• Cox E., The Fuzzy Systems Handbook (1994), ISBN 0-12-194270-8
• Elkan C.. The Paradoxical Success of Fuzzy Logic. November 1993. Available from Elkan's home page.
• Gerla G., Fuzzy logic: Mathematical Tools for Approximate Reasoning, Kluwer, 2001.
• Gottwald S., A treatase on Multi-Valued Logics, Research Studies Press LTD, Baldock 2001.
• Hájek P., Metamathematics of fuzzy logic. Kluwer 1998.
• Höppner F., Klawonn F., Kruse R. and Runkler T., Fuzzy Cluster Analysis (1999), ISBN 0-471-98864-2.
• Klaua D., Über einen Ansatz zur mehrwertigen Mengenlehre, Monatsberichte der Deutschen Akademie der Wissenschaften Berlin, vol 7 (1965), pp 859-867.
• Klir G. and Folger T., Fuzzy Sets, Uncertainty, and Information (1988), ISBN 0-13-345984-5.
• Klir G. , UTE H. St. Clair and Bo Yuan Fuzzy Set Theory Foundations and Applications,1997.
• Klir G. and Bo Yuan, Fuzzy Sets and Fuzzy Logic (1995) ISBN 0-13-101171-5
• Kosko B., Fuzzy Thinking: The New Science of Fuzzy Logic (1993), Hyperion. ISBN 0-7868-8021-X
• Novák V., Perfilieva I, Mockor J., Mathematical Principles of Fuzzy Logic, Kluwer Academic Publishers, Dordrecht, (1999).
• Yager R. and Filev D., Essentials of Fuzzy Modeling and Control (1994), ISBN 0-471-01761-2
• Zimmermann H., Fuzzy Set Theory and its Applications (2001), ISBN 0-7923-7435-5.
• Zadeh L.A., Fuzzy Sets, Information and Control, 8 (1965) 338-353.