User:John R. Brews/Sandbox: Difference between revisions

From Citizendium
Jump to navigation Jump to search
imported>John R. Brews
imported>John R. Brews
No edit summary
Line 1: Line 1:
===Interacting atoms===
{{Image|Hysteresis loops.PNG|right|200px|Add image caption here.Magnetic flux density vs. magnetic field in steel and iron; the curve depends upon the direction of traversal, the phenomenon of [[hysteresis]]}}
The outline of paramagnetism above ignores all interactions between atoms, and makes them all act individually. A natural question is: if the torque aligning atoms is due to the magnetic field in the atom's vicinity, shouldn't the field include the effect of the neighboring atoms upon the field?
In the above argument the influence of atoms upon each other was neglected. For ferromagnetic materials that approximation is invalid. The self-interaction of the atoms tends to align them even when no external magnetic field is present. As a result, ferromagnetic materials create a net magnetic field (and magnetic flux density) in the space surrounding the material, and can form permanent magnets at temperatures below the [[Curie temperature]] of the material. At higher temperatures, the aligning interaction is inadequate to overcome the randomness introduced by thermal motions.


Such a modified theory was proposed by [[Pierre-Ernest Weiss]] by introducing the notion of a ''molecular field'', a magnetic field contribution that was proportional to the magnetization in the vicinity of an atom:<ref name=Spaldin>
The figure shows ''magnetization curves'' for two different ferromagnetic materials. The curves exhibit ''hysteresis'', that is, the curve is history dependent and, in particular, depends upon the direction in which the magnetic field increases. This complex behavior indicates that magnetization in such materials is not an equilibrium process, and larger samples break up into ''magnetic domains'' or sub-regions of different magnetization directions separated by ''domain walls''.<ref name=Mayergoyz>


{{cite book |title=Magnetic materials: fundamentals and applications |author=Nicola A Spaldin |chapter=§5.2 The Curie-Weiss law |pages=p. 53 |isbn=0521886694 |year=2010 |edition=2nd ed |publisher=Cambridge University Press |url=http://books.google.com/books?id=vnrOE8pQUgIC&dq=Weiss+%22molecular+field%22&q=Curie-Weiss+molecular+field#v=onepage&q=molecular%20field&f=false}}
{{cite book |title=The Science of Hysteresis, volume III |editor=Isaak D. Mayergoyz, Giorgio Bertotti, editors |author=F Fiorillo, C Appino and M Pasquale |chapter=§1.3 Energy in a magnetic system. Domain walls and domain structures |isbn=0123694337 |year=2005 |pages=pp. 29 ''ff'' |publisher=Elsevier Academic Press |url=http://books.google.com/books?id=88W3fMqNkRwC&pg=RA2-PA29&dq=%22process+is+an+out-of-equilibrium%22&hl=en&ei=yt8ITd3hM5SssAO51MneDg&sa=X&oi=book_result&ct=result&resnum=1&ved=0CCUQ6AEwAA#v=onepage&q=%22process%20is%20an%20out-of-equilibrium%22&f=false}}


</ref>
</ref> The magnetization curve is affected (in part) by the change in size of the various domains as they adapt to changes in the external field.


:<math> \mathbf{H_W} = \gamma \mathbf M \, </math>
A simplified "toy" example of ferromagnetism helps to understand the approach. The example follows Kittel.<ref name=Kittel0>


where '''H<sub>W</sub>''' is the "Weiss field" and γ is the "molecular field constant". This contribution is added to the applied magnetic field '''H<sub>A</sub>''' to obtain the total field '''H''':
This is the same reference cited above, but a different chapter: {{cite book |author=Kittel |chapter=Chapter 12: Ferromagnetism and antiferromagnetism |title=Introduction to solid state physics |pages=pp. 321 ''ff'' |isbn=978-0-471-41526-8 |url=http://www.amazon.com/Introduction-Solid-Physics-Charles-Kittel/dp/047141526X/ref=sr_1_1?s=books&ie=UTF8&qid=1291941197&sr=1-1#reader_047141526X }}


:<math>\mathbf H = \mathbf H_A + \mathbf H_W  \ . </math>
</ref> We suppose that each atom is subject to a magnetic field due to the other atoms that is proportional to their magnetization:


Given a method to determine '''M''' from '''H''', we then find:
:<math>\mathbf{H_E} = \lambda \mathbf M \ , </math>


:<math>\mathbf M = \mathbf M (\mathbf H_A +\gamma \mathbf M ) \ , </math>
where λ is a dimensionless proportionality factor, and the subscript ''E'' stands for ''exchange field'', a technical term referring to the mechanism causing cooperation between the atoms.<ref name=exchange>
an implicit determination of '''M''' for any given '''H<sub>A</sub>'''. In particular, if we adopt the Brillouin approach based upon ''B<sub>J</sub>'' as a function of
:<math>x = \frac{g m_B J \mu_0 H}{k_B T}\ , </math>
all that is needed is to replace ''H'' with the modified ''H'' above that includes the Weiss field.


Although this approach has some application to those paramagnetic and ferrimagnetic materials that are ionic solids with localized moments, it doesn't work for ferromagnetic materials because most are metals with itinerant electrons.<ref name=Spaldin0>
The idea is that electrons obey the [[Pauli exclusion principle]] that no two can occupy the same quantum state. That means configurations with aligned spins are energetically favored over misaligned spins by an ''exchange interaction'', favoring magnetization. The same idea underlies [[Hund's rules]] for atoms, namely, other things equal, electrons in atoms populate states to maximize their total spin. Of course, an unanswered question is why ferromagnetic materials profit from this effect more than other materials. See {{cite book |title=Electrodynamics of continuous media |chapter=Chapter V: Ferromagnetism |pages=pp. 146 ''ff'' |author=LD Landau and EM Lifshitz |publisher=Pergamon Press |url=http://books.google.com/books?id=sxAJAQAAIAAJ&dq=editions%3AsxAJAQAAIAAJ&q=take+into+account+only+the+exchange+interaction#search_anchor |year=1960 |LCCN=60-14731}}, and for some simple examples {{cite book |title=Interacting electrons and quantum magnetism |author=Assa Auerbach |chapter=Chapter 2: Spin exchange |url=http://books.google.com/books?id=tiQlKzJa6GEC&pg=PA11 |pages=pp. 11 ''ff'' |isbn=0387942866 |year=1999 |publisher=Springer}}.


Chapter 9 of reference cited above: {{cite book |title=Magnetic materials: fundamentals and applications |author=Nicola A Spaldin |chapter=Chapter 9: Ferrimagnetism |pages=pp. 113 ''ff''|isbn=0521886694 |year=2010 |edition=2nd ed |publisher=Cambridge University Press |url=http://www.google.com/search?tbs=bks:1&tbo=p&q=ferrimagnets++next+section+%22molecular+field%22+inauthor:Spaldin&num=10}}
</ref> We now bootstrap the calculation of the magnetization by assuming the total magnetic field is the applied field '''H<sub>a</sub>''' ''plus'' the exchange field, and their sum induces the magnetization. Thus,
 
:<math> \mathbf M = \chi \left( \mathbf {H_a + H_E} \right) \ , </math>
 
where the approximation is made that the magnetization is simply a linear response to the magnetic field, according to the simple scalar susceptibility χ. Then with the previous expression for '''H<sub>E</sub>''',
 
:<math> \mathbf M = \chi \left( \mathbf {H_a} + \lambda \mathbf {M} \right) \ , </math>
 
or:
 
:<math> \mathbf{M} = \frac { \chi}{1-\chi \lambda } \mathbf{H_a} \ . </math>
 
Because the denominator can become small, the coefficient of '''H''' can become large, and is called the "enhanced susceptibility".<ref name= Klüber0>
 
Same reference as previously, but p. 169:{{cite book |author=J Kübler |title=Theory of itinerant electron magnetism |publisher= Oxford |isbn=0199559023 |year=2009 |edition=Revised ed |url=http://books.google.com/books?id=ZbM0gHCcmaQC&pg=PA169 |chapter=§4.1.1 Stoner theory |pages =pp. 169 ''ff''}}
 
</ref> A point of interest is that the denominator can be zero if χλ can be as large as one, which means we have an infinite magnetization with even a very small applied magnetic field. The implication is that the self-generated field can result in a magnetization ''with zero applied magnetic field''. That is the phenomenon of ferromagnetism.
 
Today it is still impossible to predict from first principles that iron is ferromagnetic.<ref name=Graham>
 
{{cite book |title=Introduction to magnetic materials |author=Bernard Dennis Cullity, Chad D. Graham |url=http://books.google.com/books?id=kk1el8vB4HoC&pg=PA131 |pages=p. 131 |isbn=0471477419 |year=2009 |publisher=Wiley-IEEE |edition=2nd ed |chapter=Chapter 4: Ferromagnetism}}
 
</ref> However, some guidance can be obtained as to which metals are candidates, and which are not, based upon estimates of how exchange energy varies with atomic radii and spacing.


</ref>


<references/>
<references/>

Revision as of 15:31, 15 December 2010

(CC) Image: John R. Brews
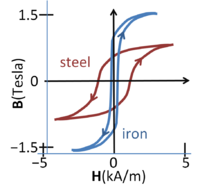
Add image caption here.Magnetic flux density vs. magnetic field in steel and iron; the curve depends upon the direction of traversal, the phenomenon of hysteresis

In the above argument the influence of atoms upon each other was neglected. For ferromagnetic materials that approximation is invalid. The self-interaction of the atoms tends to align them even when no external magnetic field is present. As a result, ferromagnetic materials create a net magnetic field (and magnetic flux density) in the space surrounding the material, and can form permanent magnets at temperatures below the Curie temperature of the material. At higher temperatures, the aligning interaction is inadequate to overcome the randomness introduced by thermal motions.

The figure shows magnetization curves for two different ferromagnetic materials. The curves exhibit hysteresis, that is, the curve is history dependent and, in particular, depends upon the direction in which the magnetic field increases. This complex behavior indicates that magnetization in such materials is not an equilibrium process, and larger samples break up into magnetic domains or sub-regions of different magnetization directions separated by domain walls.[1] The magnetization curve is affected (in part) by the change in size of the various domains as they adapt to changes in the external field.

A simplified "toy" example of ferromagnetism helps to understand the approach. The example follows Kittel.[2] We suppose that each atom is subject to a magnetic field due to the other atoms that is proportional to their magnetization:

where λ is a dimensionless proportionality factor, and the subscript E stands for exchange field, a technical term referring to the mechanism causing cooperation between the atoms.[3] We now bootstrap the calculation of the magnetization by assuming the total magnetic field is the applied field Ha plus the exchange field, and their sum induces the magnetization. Thus,

where the approximation is made that the magnetization is simply a linear response to the magnetic field, according to the simple scalar susceptibility χ. Then with the previous expression for HE,

or:

Because the denominator can become small, the coefficient of H can become large, and is called the "enhanced susceptibility".[4] A point of interest is that the denominator can be zero if χλ can be as large as one, which means we have an infinite magnetization with even a very small applied magnetic field. The implication is that the self-generated field can result in a magnetization with zero applied magnetic field. That is the phenomenon of ferromagnetism.

Today it is still impossible to predict from first principles that iron is ferromagnetic.[5] However, some guidance can be obtained as to which metals are candidates, and which are not, based upon estimates of how exchange energy varies with atomic radii and spacing.


  1. ↑ F Fiorillo, C Appino and M Pasquale (2005). “§1.3 Energy in a magnetic system. Domain walls and domain structures”, Isaak D. Mayergoyz, Giorgio Bertotti, editors: The Science of Hysteresis, volume III. Elsevier Academic Press, pp. 29 ff. ISBN 0123694337. 
  2. ↑ This is the same reference cited above, but a different chapter: Kittel. “Chapter 12: Ferromagnetism and antiferromagnetism”, Introduction to solid state physics, pp. 321 ff. ISBN 978-0-471-41526-8. 
  3. ↑ The idea is that electrons obey the Pauli exclusion principle that no two can occupy the same quantum state. That means configurations with aligned spins are energetically favored over misaligned spins by an exchange interaction, favoring magnetization. The same idea underlies Hund's rules for atoms, namely, other things equal, electrons in atoms populate states to maximize their total spin. Of course, an unanswered question is why ferromagnetic materials profit from this effect more than other materials. See LD Landau and EM Lifshitz (1960). “Chapter V: Ferromagnetism”, Electrodynamics of continuous media. Pergamon Press, pp. 146 ff. , and for some simple examples Assa Auerbach (1999). “Chapter 2: Spin exchange”, Interacting electrons and quantum magnetism. Springer, pp. 11 ff. ISBN 0387942866. .
  4. ↑ Same reference as previously, but p. 169:J Kübler (2009). “§4.1.1 Stoner theory”, Theory of itinerant electron magnetism, Revised ed. Oxford, pp. 169 ff. ISBN 0199559023. 
  5. ↑ Bernard Dennis Cullity, Chad D. Graham (2009). “Chapter 4: Ferromagnetism”, Introduction to magnetic materials, 2nd ed. Wiley-IEEE, p. 131. ISBN 0471477419. 
Retrieved from "https://citizendium.org/wiki/index.php?title=User:John_R._Brews/Sandbox&oldid=816684"